Western tactical neutron bombs were disarmed after Russian propaganda lie. Russia now has over 2000 ... a reposting of the 2022 post with improvements & revisions NUKEGATE (updated: 2024)
(For the essential so-called "overkill" background or Sir Slim's "the more you use, fewer you lose" success formula for winning in Burma against Japan - where physicist Herman Kahn served while his friend Sam Cohen was calculating nuclear weapon efficiencies at the Los Alamos Manhattan Project, which again used "overkill" to convince the opponent to throw in the towel - please see my post on the practicalities of really DETERRING WWIII linked here.)
ABOVE: Russian 1985 1st Cold War SLBM first strike plan. The initial use of Russian SLBM launched nuclear missiles from off-coast against command and control centres (i.e. nuclear explosions to destroy warning satellite communications centres by radiation on satellites as well as EMP against ground targets, rather than missiles launched from Russia against cities, as assumed by 100% of the Cold War left-wing propaganda) is allegedly a Russian "fog of war" strategy. Such a "demonstration strike" is aimed essentially at causing confusion about what is going on, who is responsible - it is not quick or easy to finger-print high altitude bursts fired by SLBM's from submerged submarines to a particular country because you don't get fallout samples to identify isotopic plutonium composition. Russia could immediately deny the attack (implying, probably to the applause of the left-wingers that this was some kind of American training exercise or computer based nuclear weapons "accident", similar to those depicted in numerous anti-nuclear Cold War propaganda films). Thinly-veiled ultimatums and blackmail follow. America would not lose its population or even key cities in such a first strike (contrary to left-wing propaganda fiction), as with Pearl Harbor in 1941; it would lose its complacency and its sense of security through isolationism, and would either be forced into a humiliating defeat or a major war.
Before 1941, many warned of the risks but were dismissed on the basis that Japan was a smaller country with a smaller economy than the USA and war was therefore absurd (similar to the way Churchill's warnings about European dictators were dismissed by "arms-race opposing pacifists" not only in the 1930s, but even before WWI; for example Professor Cyril Joad documents in the 1939 book "Why War?" his first hand witnessing of Winston Churchill's pre-WWI warning and call for an arms-race to deter that war by the sneering Norman Angell). It is vital to note that there is an immense pressure against warnings of Russian nuclear superiority even today, most of it contradictory. E.g. the left wing (Russian biased) "experts" whose voices are the only ones reported in the Western media (traditionally led by "Scientific American" and "Bulletin of the Atomic Scientists"), simultaneously claim Russia imposes such a complex SLBM and ICBM threat that we must disarm now, while also claiming that their tactical nuclear weapons probably won't work so aren't a threat! In similar vein, Teller-critic Hans Bethe also used to falsely "dismiss" Russian nuclear superiority by claiming (with any more evidence than Brezhnev's word, it appeared) that Russian delivery systems are "less accurate" than Western missiles (as if accuracy has anything to do with high altitude EMP strikes, where the effects cover thousands of miles radii). Such claims would then by repeatedly endlessly in the Western media by Russian biased "journalists" or agents of influence, and any attempt to point out the propaganda would turn into a "Reds under beds" argument, designed to imply that the truth is dangerous to "peaceful coexistence"!
The Top Secret American intelligency report NIE 11-3/8-74 "Soviet Forces for Intercontinental Conflict" warned on page 6: "the USSR has largely eliminated previous US quantitative advantages in strategic offensive forces." page 9 of the report estimated that the Russian's ICBM and SLBM launchers exceed the USAs 1,700 during 1970, while Russia's on-line missile throw weight had exceeded the USA's one thousand tons back in 1967! Because the USA had more long-range bombers which can carry high-yield bombs than Russia (bombers are more vulnerable to air defences so were not Russia's priority), it took a little longer for Russia to exceed the USA in equivalent megatons, but the 1976 Top Secret American report NIE 11-3/8-76 at page 17 shows that in 1974 Russia exceeded the 4,000 equivalent-megatons payload of USA missiles and aircraft (with less vulnerability for Russia, since most of Russia's nuclear weapons were on missiles not in SAM-vulnerable aircraft), amd by 1976 Russia could deliver 7,000 tons of payload by missiles compared to just 4,000 tons on the USA side. These reports were kept secret for decades to protect the intelligence sources, but they were based on hard evidence. For example, in August 1974 the Hughes Aircraft Company used a specially designed ship (Glomar Explorer, 618 feet long, developed under a secret CIA contract) to recover nuclear weapons and their secret manuals from a Russian submarine which sank in 16,000 feet of water, while in 1976 America was able to take apart the electronics systems in a state-of-the-art Russian MIG-25 fighter which was flown to Japan by defector Viktor Belenko, discovering that it used exclusively EMP-hard miniature vacuum tubes with no EMP-vulnerable solid state components.
Update: Lawrence Livermore National Laboratory's $3.5 billion National Ignition Facility, NIF, using ultraviolet wavelength laser beam pulses of 2MJ on to a 2mm diameter spherical beryllium shell of frozen D+T inside a 1 cm-long hollow gold cylinder "hohlraum" (which is heated to a temperature where it then re-radiates energy at much higher frequency, x-rays, on to the surface of the beryllium ablator of the central fusion capsule, which ablates causing it to recoil inward (as for the 1962 Ripple II nuclear weapon's secondary stage, the capsule is compressed by a factor of 35, mimicking the isentropic compression mechanism of a miniature Ripple II clean nuclear weapon secondary stage), has now repeatedly achieved nuclear fusion explosions of over 3MJ, equivalent to nearly 1 kg of TNT explosive. According to a Time article (linked her) about fusion system designer Annie Kritcher, the recent breakthrough was in part due to using a ramping input energy waveform: "success that came thanks to tweaks including shifting more of the input energy to the later part of the laser shot", a feature that minimises the rise in entropy due to shock shock wave generation (which heats the capsule, causing it to expand and resist compression) and increases isentropic compression which was the principle used by LLNL's J. H. Nuckolls to achieve the 99.9% clean Ripple II 9.96 megaton nuclear test success in Dominic-Housatonic on 30 October 1962. Nuckolls in 1972 published the equation for the idealized input power waveform required for isentropic, optimized compression of fusion fuel (Nature, v239, p139): P ~ (1 - t)-1.875, where t is time in units of the transit time (the time taken for the shock to travel to the centre of the fusion capsule), and -1.875 a constant based on the specific heat of the ionized fuel (Nuckolls has provided the basic declassified principles, see extract linked here).
In a fission primary, speed of compression is of the essence in order to beat pre-initiation (where a stray spontaneous fission neutron from Pu-240 or Pu-242 impurities sets off the chain reaction before maximum compression is obtained, reducing the yield). But this danger is not possible when compressing a 100% fusion capsule, where speed is not the key, and fusion is automatically initiated when the compression squeezes the D+T to an adequate density. Provided that the compression mechanism is efficient for fusion, time is not of the essence. The fusion burn efficiency is a function of the compression attained, rather than the speed of implosion. To be clear, the energy reliably released by the 2mm diameter capsule of fusion fuel was roughly a 1 kg TNT explosion. 80% of this is in the form of 14.1 MeV neutrons (ideal for fissioning lithium-7 in LiD to yield more tritium), and 20% is the kinetic energy of fused nuclei (which is quickly converted into x-rays radiation energy by collisions). If this neutron and x-ray energy can be coupled by a scattering container into a small second stage of Li6D, it will be possible to set off a multiplicative chain reaction of fusion capsule stages, rapidly increasing the total fusion energy release. Nuckolls' 9.96 megaton Housatonic (10 kt Kinglet primary and 9.95 Mt Ripple II 100% clean isentropically compressed secondary) of 1962 proved that it is possible to use multiplicative staging whereby lower yield primary nuclear explosions trigger off a fusion stage 1,000 times more powerful than its initiator. OK, the first laser fusion ignitions last year only multiplied the supplied input energy by a factor that's closer to 2 than to the impressive 1,000 of the 1962 Ripple II nuclear warhead, but the problems and solutions are known and the whole basis of NIF for practical fusion power is improve this technology. (The first computers were far more than 1,000 times as bulky and less efficient than those available after a few years of very hard-graft research and development.) Even if initial-stage multiplications are far lower than 1,000, you can simply add more small stages to get around this (they are tiny and won't take up a huge volume or mass in the warhead). The later stages will definitely have less asymmetry problems (as in Ripple II), and we know from the Ripple II test back in 1962 that you can definitely multiply by a factor of 1,000 to get from 10 kilotons to 10 megatons in a single multiplicative stage! Another key factor, as shown on our graph linked here, is that you can use cheap natural LiD as fuel once you have a successful D+T reaction, because naturally abundant, cheap Li-7 more readily fissions to yield tritium with the 14.1 MeV neutrons from D+T fusion, than expensively enriched Li-6, which is needed to make tritium in nuclear reactors where the fission neutron energy of around 1 MeV is too low to to fission Li-7.
It should also be noted that despite an openly published paper about Nuckolls' Ripple II success being stymied in 2021 by Jon Grams, the subject is still being covered up/ignored by the anti-nuclear biased Western media! Grams article fails to contain the design details such as the isentropic power delivery curve etc from Nuckolls' declassified articles that we include in the latest blog post here. One problem regarding "data" causing continuing confusion about the Dominic-Housatonic 30 October 1962 Ripple II test at Christmas Island, is made clear in the DASA-1211 report's declassified summary of the sizes, weights and yields of those tests: Housatonic was Nuckolls' fourth and final isentropic test, with the nuclear system inserted into a heavy steel Mk36 drop case, making the overall size 57.2 inches in diameter, 147.9 long and 7,139.55 lb mass, i.e. 1.4 kt/lb or 3.0 kt/kg yield-to-mass ratio for 9.96 Mt yield, which is not impressive for that yield range until you consider (a) that it was 99.9% fusion and (b) the isentropic design required a heavy holhraum around the large Ripple II fusion secondary stage to confine x-rays for relatively long time during which a slowly rising pulse of x-rays were delivered from the primary to secondary via a very large areas of foam elsewhere in the weapon, to produce isentropic compression. Additionally, the test was made in a hurry before an atmospheric teat ban treaty, and this rushed use of a standard air drop steel casing made the tested weapon much heavier than a properly weaponized Ripple II. The key point is that a 10 kt fission device set off a ~10 Mt fusion explosion, a very clean deterrent. Applying this Ripple II 1,000-factor multiplicative staging figure directly to this technology for clean nuclear warheads, a 0.5 kg TNT D+T fusion capsule would set off a 0.5 ton TNT 2nd stage of LiD, which would then set off a 0.5 kt 3rd stage "neutron bomb", which could then be used to set off a 500 kt 4th stage or "strategic nuclear weapon". It is therefore now possible not just in principle but in practice, using suitable already-proved technical staging systems used in 1960s nuclear weapon tests successfully, to design 100% clean fusion nuclear warheads! Yes, the details have been worked out, yes the technology has been tested in piecemeal fashion. All that is now needed is a new, but quicker and cheaper, Star Wars program or Manhattan Project style effort to pull the components together. This will constitute a major leap forward in the credibility of the deterrence of aggressors.
ABOVE: as predicted, the higher the x-ray input laser pulse for the D+T initiator of a clean multiplicatively-staged nuclear deterrent, the lower the effect of plasma instabilities and asymmetries and the greater the fusion burn. To get ignition (where the x-ray energy injected into the fusion hohlraum by the laser is less than the energy released in the D+T fusion burn) they have had to use about 2 MJ delivered in 10 ns or so, equivalent to 0.5 kg of TNT equivalent. But for deterrent use, why use such expensive, delicate x-ray lasers? Why not just use one-shot miniaturised x-ray tubes with megavolt electron acceleration, powered a suitably ramped pulse from a chemical explosion for magnetic flux compression current generation? At 10% efficiency, you need 0.5 x 10 = 5 kg of TNT! Even at 1% efficiency, 50 kg of TNT will do. Once the D+T gas capsule's hohlraum is well over 1 cm in size, to minimise the risk of imperfections that cause asymmetries, you don't any longer need focussed laser beams to enter tiny apertures. You might even be able to integrate many miniature flash x-ray tubes (each designed to burn out when firing one pulse of a MJ or so) into a special hohlraum. Humanity urgently needs a technological arms race akin to Reagan's Star Wars project, to deter the dictators from invasions and WWIII. In the conference video above, a question was asked about the real efficiency of the enormous repeat-pulse capable laser system's efficiency (not required for a nuclear weapon whose components only require the capability to be used once, unlike lab equipment): the answer is that 300 MJ was required by the lab lasers to fire a 2 MJ pulse into the D+T capsule's x-ray hohlraum, i.e. their lasers are only 0.7% efficient! So why bother? We know - from the practical use of incoherent fission primary stage x-rays to compress and ignite fusion capsules in nuclear weapons - that you simply don't need coherent x-rays from a laser for this purpose. The sole reason they are approaching the problem with lasers is that they began their lab experiments decades ago with microscopic sized fusion capsules and for those you need a tightly focussed beam to insert energy through a tiny hohlraum aperture. But now they are finally achieving success with much larger fusion capsules (to minimise instabilities that caused the early failures), it may be time to change direction. A whole array of false "no-go theorems" can and will be raised by ignorant charlatan "authorities" against any innovation; this is the nature of the political world. There is some interesting discussion of why clean bombs aren't in existence today, basically the idealized theory (which works fine for big H-bombs but ignores small-scale asymmetry problems which are important only at low ignition energy) understimated the input energy required for fusion ignition by a factor of 2000:
"The early calculations on ICF (inertial-confinement fusion) by John Nuckolls in 1972 had estimated that ICF might be achieved with a driver energy as low as 1 kJ. ... In order to provide reliable experimental data on the minimum energy required for ignition, a series of secret experiments—known as Halite at Livermore and Centurion at Los Alamos—was carried out at the nuclear weapons test site in Nevada between 1978 and 1988. The experiments used small underground nuclear explosions to provide X-rays of sufficiently high intensity to implode ICF capsules, simulating the manner in which they would be compressed in a hohlraum. ... the Halite/Centurion results predicted values for the required laser energy in the range 20 to 100MJ—higher than the predictions ..." - Garry McCracken and Peter Stott, Fusion, Elsevier, 2nd ed., p149.
In the final diagram above, we illustrate an example of what could very well occur in the near future, just to really poke a stick into the wheels of "orthodoxy" in nuclear weapons design: is it possible to just use a lot of (perhaps hardened for higher currents, perhaps no) pulsed current driven microwave tubes from kitchen microwave ovens, channelling their energy using waveguides (simply metal tubes, i.e. electrical Faraday cages, which reflect and thus contain microwaves) into the hohlraum, and make the pusher of dipole molecules (like common salt, NaCl) which is a good absorber of microwaves (as everybody knows from cooking in microwave ovens)? It would be extremely dangerous, not to mention embarrassing, if this worked, but nobody had done any detailed research into the possibility due to groupthink orthodoxy and conventional boxed in thinking! Remember, the D+T capsule just needs extreme compression and this can be done by any means that works. Microwave technology is now very well-established. It's no good trying to keep anything of this sort "secret" (either officially or unofficially) since as history shows, dictatorships are the places where "crackpot"-sounding ideas (such as douple-primary Project "49" Russian thermonuclear weapon designs, Russian Sputnik satellites, Russian Novichok nerve agent, Nazi V1 cruise missiles, Nazi V2 IRBM's, etc.) can be given priority by loony dictators. We have to avoid, as Edward Teller put it (in his secret commentary debunking Bethe's false history of the H-bomb, written AFTER the Teller-Ulam breakthrough), "too-narrow" thinking (which Teller said was still in force on H-bomb design even then). Fashionable hardened orthodoxy is the soft underbelly of "democracy" (a dictatorship by the majority, which is always too focussed on fashionable ideas and dismissive of alternative approaches in science and technology). Dictatorships (minorities against majorities) have repeatedly demonstrated a lack of concern for the fake "no-go theorems" used by Western anti-nuclear "authorities" to ban anything but fashionable groupthink science.
In the diagram below, it appears that the Mk17 only had a single secondary stage like the similar yield 1952 Mike design. The point here is that popular misunderstanding of the simple mechanism of x-ray energy transfer for higher yield weapons may be creating a dogmatic attitude even in secret nuclear weaponeer design labs, where orthodoxy is followed too rigorously. The Russians (see quotes on the latest blog post here) state they used two entire two-stage thermonuclear weapons with a combined yield of 1 megaton to set off their 50 megaton test in 1961. If true, you can indeed use two-stage hydrogen bombs as an "effective primary" to set off another secondary stage, of much higher yield. Can this be reversed in the sense of scaling it down so you have several bombs-within-bombs, all triggered by a really tiny first stage? In other words, can it be applied to neutron bomb design?
Update (15 Dec 2023): PDF uploaded of UK DAMAGE BY NUCLEAR WEAPONS (linked here on Internet Archive) - secret 1000 pages UK and USA nuclear weapon test effects analysis, and protective measures determined at those tests (not guesswork) relevant to escalation threats by Russia for EU invasion (linked here at wordpress) in response to Ukraine potentially joining the EU (this is now fully declassified without deletions, and in the UK National Archives at Kew):
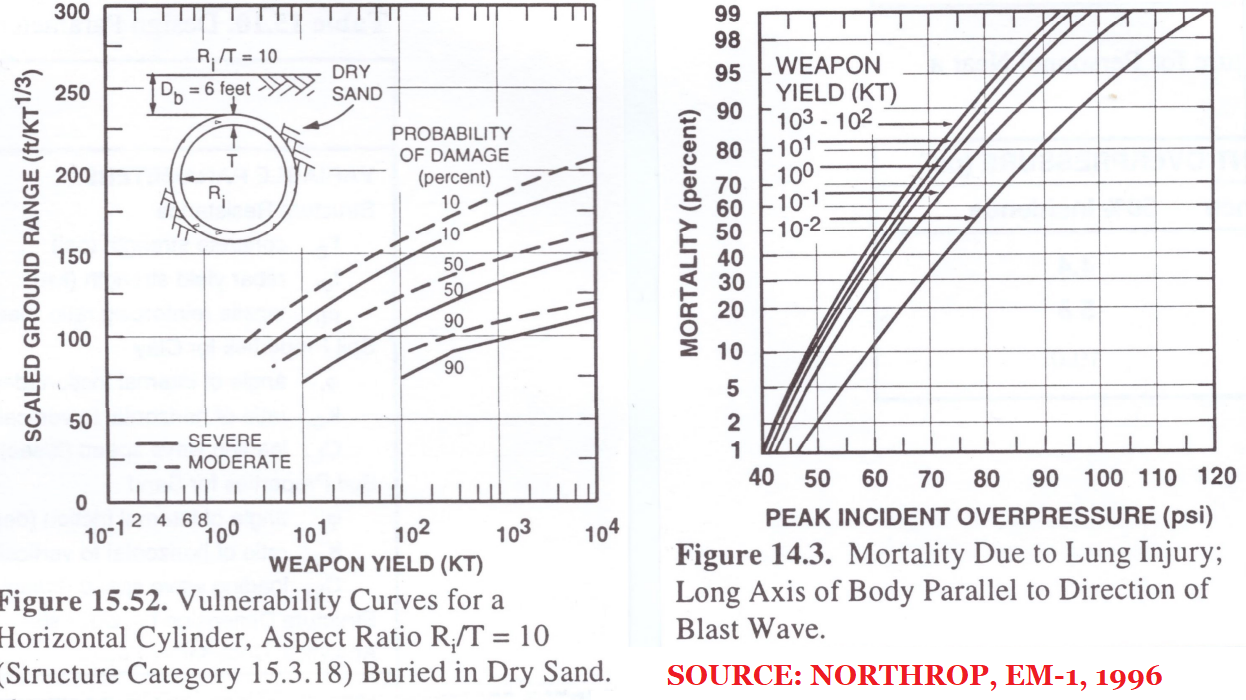
ABOVE: some pages from the originally SECRET ATOMIC 1,000 pages long UK Government Damage by Nuclear Weapons manual (now totally declassified without any deletions of data - unlike American manuals - in the UK National Archives, Kew), summarizing all of the effects data from 1950s British and American atmospheric nuclear weapons tests on military targets and also civil defense shelters tests, costs and safety. Below: some extracts from reports on Australian-British nuclear weapon test operations at Maralinga in 1956 and 1957, Buffalo and Antler, proved that even at 10 psi peak overpressure for the 15 kt Buffalo-1 shot, the dummy lying prone facing the blast was hardly moved due to the low cross-sectional area exposed to the blast winds, relative to standing dummies which were severely displaced and damaged. The value of trenches in protecting personnel against blast winds and radiation was also proved in tests (gamma radiation shielding of trenches had been proved at an earlier nuclear test in Australian, Operation Hurricane in 1952). (Antler report linked here; Buffalo report linked here.) All of this is still omitted from the American Glasstone and Dolan book "The Effects of Nuclear Weapons". The 1996 Northrop EM-1 (see extracts below showing protection by modern buildings and also simple shelters very close to nuclear tests; note that Northrop's entire set of damage ranges as a function of yield for underground shelters, tunnels, silos are based on two contained deep underground nuclear tests of different yield scaled to surface burst using the assumption of 5% yield ground coupling relative to the underground shots; this 5% equivalence figure appears to be an exaggeration for compact modern warheads, e.g. the paper “Comparison of Surface and Sub-Surface Nuclear Bursts,” from Steven Hatch, Sandia National Laboratories, to Jonathan Medalia, October 30, 2000, shows a 2% equivalence, e.g. Hatch shows that 1 megaton surface burst produces identical ranges to underground targets as a 20 kt burst at >20m depth of burst, whereas Northrop would require 50kt) has not been openly published, despite such protection being used in Russia! This proves heavy bias against credible tactical nuclear deterrence of the invasions that trigger major wars that could escalate into nuclear war (Russia has 2000+ dedicated neutron bombs; we don't!) and against simple nuclear proof tested civil defence which makes such deterrence credible and of course is also of validity against conventional wars, severe weather, peacetime disasters, etc. The basic fact is that nuclear weapons can deter/stop invasions unlike the conventional weapons that cause mass destruction, and nuclear collateral damage is eliminated easily for nuclear weapons by using them on military targets, since at collateral damage distances all the effects are sufficiently delayed in arrival (unlike the case for the smaller areas affected by conventional weapons). As for Hitler's stockpile of 12,000 tons of tabun nerve gas, whose use was deterred by proper defences (gas masks for all civilians, as well as biological agent anthrax and mustard gas retaliation capacity), it is possible to deter escalation within a world war with a crazy terrorist if people are protected by defence and deterrence:
J. R. Oppenheimer (opposing Teller), February 1951: "It is clear that they can be used only as adjuncts in a military campaign which has some other components, and whose purpose is a military victory. They are not primarily weapons of totality or terror, but weapons used to give combat forces help they would otherwise lack. They are an integral part of military operations. Only when the atomic bomb is recognized as useful insofar as it is an integral part of military operations, will it really be of much help in the fighting of a war, rather than in warning all mankind to avert it." (Quotation: Samuel Cohen, Shame, 2nd ed., 2005, page 99.)
‘The Hungarian revolution of October and November 1956 demonstrated the difficulty faced even by a vastly superior army in attempting to dominate hostile territory. The [Soviet Union] Red Army finally had to concentrate twenty-two divisions in order to crush a practically unarmed population. ... With proper tactics, nuclear war need not be as destructive as it appears when we think of [World War II nuclear city bombing like Hiroshima]. The high casualty estimates for nuclear war are based on the assumption that the most suitable targets are those of conventional warfare: cities to interdict communications ... With cities no longer serving as key elements in the communications system of the military forces, the risks of initiating city bombing may outweigh the gains which can be achieved. ...
‘The elimination of area targets will place an upper limit on the size of weapons it will be profitable to use. Since fall-out becomes a serious problem [i.e. fallout contaminated areas which are so large that thousands of people would need to evacuate or shelter indoors for up to two weeks] only in the range of explosive power of 500 kilotons and above, it could be proposed that no weapon larger than 500 kilotons will be employed unless the enemy uses it first. Concurrently, the United States could take advantage of a new development which significantly reduces fall-out by eliminating the last stage of the fission-fusion-fission process.’
- Dr Henry Kissinger, Nuclear Weapons and Foreign Policy, Harper, New York, 1957, pp. 180-3, 228-9.
(Quoted in 2006 on this blog here.)
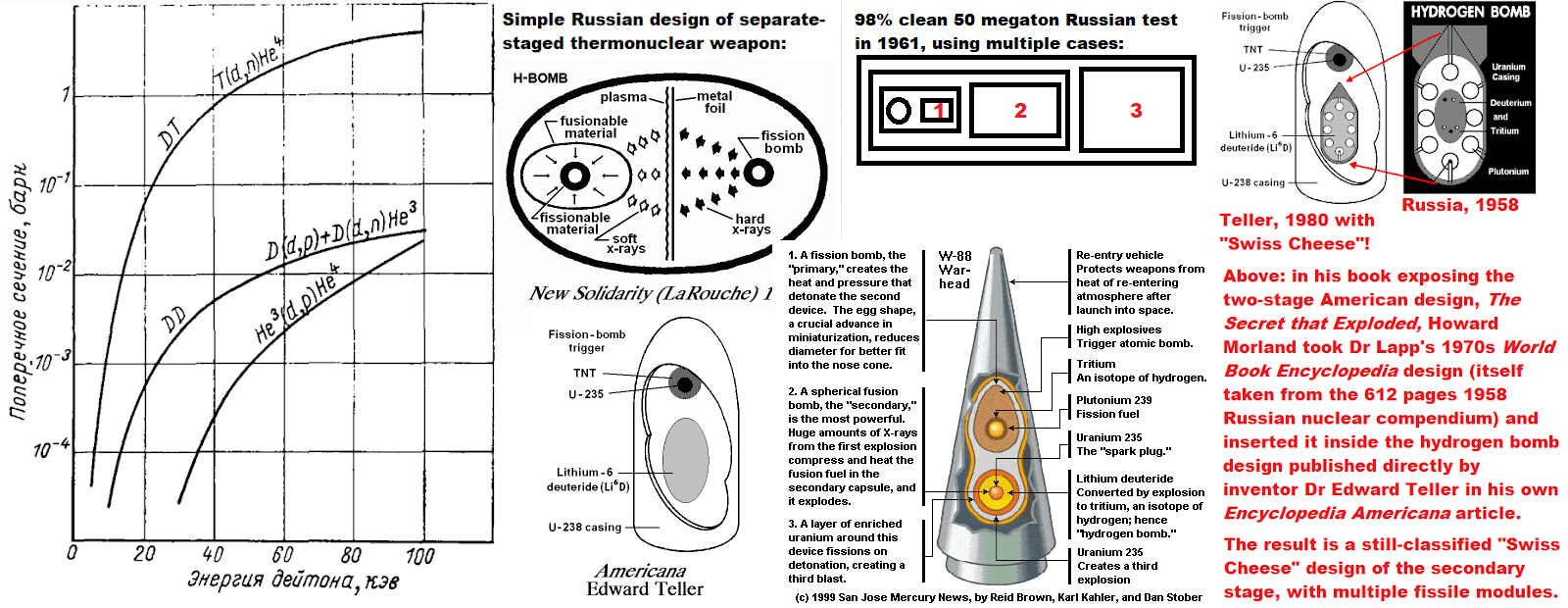
ABOVE: 16 February 1950 Daily Express editorial on H Bomb problem due to the fact that the UN is another virtue signalling but really war mongering League of Nations (which oversaw Nazi appeasement and the outbreak of WWII); however Fuchs had attended the April 1946 Super Conference during which the Russian version of the H-bomb involving isentropic radiation implosion of a separate low-density fusion stage (unlike Teller's later dense metal ablation rocket implosion secondary TX14 Alarm Clock and Sausage designs) were discussed and then given to Russia. The media was made aware only that Fuchs hade given the fission bomb to Russia. The FBI later visited Fuchs in British jail, showed him a film of Harry Gold (whom Fuchs identified as his contact while at Los Alamos) and also gave Fuchs a long list of secret reports to mark off individually so that they knew precisely what Stalin had been given. Truman didn't order H-bomb research and development because Fuchs gave Stalin the A-bomb, but because he gave them the H-bomb. The details of the Russian H-bomb are still being covered up by those who want a repetition of 1930s appeasement, or indeed the deliberate ambiguity of the UK Cabinet in 1914 which made it unclear what the UK would do if Germany invaded Belgium, allowing the enemy to exploit that ambiguity, starting a world war. The key fact usually covered up (Richard Rhodes, Chuck Hansen, and the whole American "expert nuclear arms community" all misleadingly claim that Teller's Sausage H-bomb design with a single primary and a dense ablator around a cylindrical secondary stage - uranium, lead or tungsten - is the "hydrogen bomb design") here is that two attendees of the April 1946 Super Conference, the report author Egon Bretscher and the radiation implosion discoverer Klaus Fuchs - were British, and both contributed key H-bomb design principles to the Russian and British weapons (discarded for years by America). Egon Bretscher for example wrote up the Super Conference report, during which attendees suggested various ways to try to achieve isentropic compression of low-density fusion fuel (a concept discarded by Teller's 1951 Sausage design, but used by Russia and re-developed in America on Nuckolls 1962 Ripple tests), and after Teller left Los Alamos, Bretscher took over work on Teller's Alarm Clock layered fission-fusion spherical hybrid device before Bretscher himself left Los Alamos and became head of nuclear physics at Harwell, UK,, submitting UK report together with Fuchs (head of theoretical physics at Harwell) which led to Sir James Chadwick's UK paper on a three-stage thermonuclear Super bomb which formed the basis of Penney's work at the UK Atomic Weapons Research Establishment. While Bretscher had worked on Teller's hybrid Alarm Clock (which originated two months after Fuchs left Los Alamos), Fuchs co-authored a hydrogen bomb patent with John von Neumann, in which radiation implosion and ionization implosion was used. Between them, Bretscher and Fuchs had all the key ingredients. Fuchs leaked them to Russia and the problem persists today in international relations.
There are four ways of dealing with aggressors: conquest (fight them), intimidation (deter them), fortification (shelter against their attacks; historically used as castles, walled cities and even walled countries in the case of China's 1,100 mile long Great Wall and Hadrian's Wall, while the USA has used the Pacific and Atlantic as successful moats against invasion, at least since Britain invaded Washington D.C. back in 1812), and friendship (which if you are too weak to fight, means appeasing them, as Chamberlain shook hands with Hitler for worthless peace promises). These are not mutually exclusive: you can use combinations. If you are very strong in offensive capability and also have walls to protect you while your back is turned, you can - as Teddy Roosevelt put it (quoting a West African proverb): "Speak softly and carry a big stick." But if you are weak, speaking softly makes you a target, vulnerable to coercion. This is why we don't send troops directly to Ukraine. When elected in 1960, Kennedy introduced "flexible response" to replace Dulles' "massive retaliation", by addressing the need to deter large provocations without being forced to decide between the unwelcome options of "surrender or all-out nuclear war" (Herman Kahn called this flexible response "Type 2 Deterrence"). This was eroded by both Russian civil defense and their emerging superiority in the 1970s: a real missiles and bombers gap emerged in 1972 when the USSR reached and then exceeded the 2,200 of the USA, while in 1974 the USSR achieve parity at 3,500 equivalent megatons (then exceeded the USA), and finally today Russia has over 2,000 dedicated clean enhanced neutron tactical nuclear weapons and we have none (except low-neutron output B61 multipurpose bombs). (Robert Jastrow's 1985 book How to make nuclear Weapons obsolete was the first to have graphs showing the downward trend in nuclear weapon yields created by the development of miniaturized MIRV warheads for missiles and tactical weapons: he shows that the average size of US warheads fell from 3 megatons in 1960 to 200 kilotons in 1980, and from a total of 12,000 megatons in 1960 to 3,000 megatons in 1980.)
The term "equivalent megatons" roughly takes account of the fact that the areas of cratering, blast and radiation damage scale not linearly with energy but as something like the 2/3 power of energy release; but note that close-in cratering scales as a significantly smaller power of energy than 2/3, while blast wind drag displacement of jeeps in open desert scales as a larger power of energy than 2/3. Comparisons of equivalent megatonnage shows, for example, that WWII's 2 megatons of TNT in the form of about 20,000,000 separate conventional 100 kg (0.1 ton) explosives is equivalent to 20,000,000 x (10-7)2/3 = 431 separate 1 megaton explosions! The point is, nuclear weapons are not of a different order of magnitude to conventional warfare, because: (1) devastated areas don't scale in proportion to energy release, (2) the number of nuclear weapons is very much smaller than the number of conventional bombs dropped in conventional war, and (3) because of radiation effects like neutrons and intense EMP, it is possible to eliminate physical destruction by nuclear weapons by a combination of weapon design (e.g. very clean bombs like 99.9% fusion Dominic-Housatonic, or 95% fusion Redwing-Navajo) and burst altitude or depth for hard targets, and create a weapon that deters invasions credibly (without lying local fallout radiation hazards), something none of the biased "pacifist disarmament" lobbies (which attract Russian support) tell you! There's a big problem with propaganda here.
ILLUSTRATION: the threat of WWII and the need to deter it was massively derided by popular pacifism which tended to make "jokes" of the Nazi threat until too late (example of 1938 UK fiction on this above; Charlie Chaplin's film "The Great Dictator" is another example), so three years after the Nuremberg Laws and five years after illegal rearmament was begun by the Nazis, in the UK crowds of "pacifists" in Downing Street, London, support friendship with the top racist, dictatorial Nazis in the name of "world peace". The Prime Minister used underhand techniques to try to undermine appeasement critics like Churchill and also later to get W. E. Johns fired from both editorships of Flying (weekly) and Popular Flying (monthly) to make it appear everybody "in the know" agreed with his actions, hence the contrived "popular support" for collaborating with terrorists depicted in these photos. The same thing persists today; in the 1920s and 1930s "pacifist" was driven by claims explosions, fire and poison gas will kill everybody in a knockout blow immediately war breaks out.
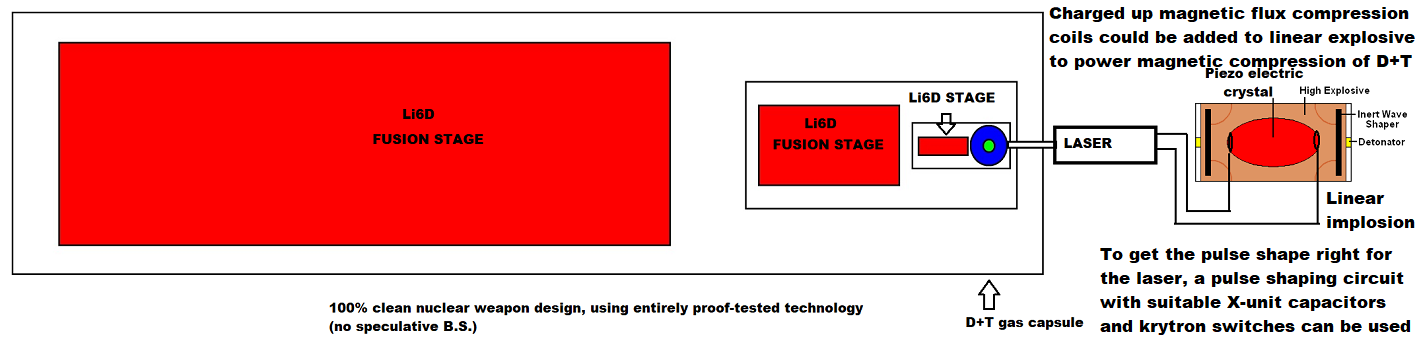
Update (30 January 2024): on the important world crisis, https://vixra.org/abs/2312.0155 gives a detailed review of "Britain and the H-bomb" (linked here), and why the "nuclear deterrence issue" isn't about "whether we should deter evil", but precisely what design of nuclear warhead we should have in order to do that cheaply, credibly, safely, and efficiently without guaranteeing either escalation or the failure of deterrence. When we disarmed our chemical and biological weapons, it was claimed that the West could easily deter those weapons using strategic nuclear weapons to bomb Moscow (which has shelters, unlike us). That failed when Putin used sarin and chlorine to prop up Assad in Syria, and Novichok in the UK to kill Dawn Sturgess in 2018. So it's just not a credible deterrent to say you will bomb Moscow if Putin invades Europe or uses his 2000 tactical nuclear weapons. An even more advanced deterrent, the 100% clean very low yield (or any yield) multiplicative staged design without any fissile material whatsoever, just around the corner. Clean secondary stages have been proof-tested successfully for example in the 100% clean Los Alamos Redwing Navajo secondary, and the 100% clean Ripple II secondary tested 30 October 1962, and the laser ignition of very tiny fusion capsules to yield more energy than supplied has been done on 5 December 2022 when a NIF test delivered 2.05 MJ (the energy of about 0.5 kg of TNT) to a fusion capsule which yielded 3.15 MJ, so all that is needed is to combine both ideas in a system whereby suitably sized second stages - ignited in the first place by a capacitative charged circuit sending a pulse of energy to a suitable laser system (the schematic shown is just a sketch of principle - more than one laser would possibly be required for reliability of fusion ignition) acting on tiny fusion capsule as shown - are encased to two-stage "effective primaries" which each become effective primaries of bigger systems, thus a geometric series of multiplicative staging until the desired yield is reached. Note that the actual tiny first T+D capsule can be compressed by one-shot lasers - compact lasers used way beyond their traditional upper power limit and burned out in a firine a single pulse - in the same way the gun assembly of the Hiroshima bomb was based on a one-shot gun. In other words, forget all about textbook gun design. The Hiroshima bomb gun assembly system only had to be fired once unlike a field artillery piece which has to be fired many thousands of times before metal fatigue sets in. Thus, by analogy, the lasers - which can be powered by ramping current pulses from magnetic flux compressor systems - for use in a clean bomb will be much smaller and lighter than current lab gear which is designed to be used thousands of times in repeated experiments. The diagram below shows cylindrical Li6D stages throughout for a compact bomb shape, but spherical stages can be used, and once a few stages get fired, the flux of 14 MeV neutrons is sufficient to go to cheap natural LiD. To fit it into a MIRV warhead, the low density of LiD constrains such a clean warhead will have a low nuclear yield, which means a tactical Cohen type neutron deterrent of the invasions that cause big wars. It should also be noted that in 1944 von Neumann suggested that T + D inside the core of the fission weapon would be compressed by "ionization compression" during fission (where a higher density ionized plasma compresses a lower density ionized plasma, i.e. the D + T plasma), an idea that was - years later - named the Internal Booster principle by Teller; see Frank Close, "Trinity", Allen Lane, London, 2019, pp158-159 where Close argues that during the April 1946 Superbomb Conference, Fuchs extended von Neumann's 1944 internal fusion boosting idea to an external D + T filled BeO walled capsule:
"Fuchs reasoned that [the very low energy, 1-10 kev, approximately 10-100 lower energy than medical] x-rays from the [physically separated] uranium explosion would reach the tamper of beryllium oxide, heat it, ionize the constituents and cause them to implode - the 'ionization implosion' concept of von Neumann but now applied to deuterium and tritium contained within beryllium oxide. To keep the radiation inside the tamper, Fuchs proposed to enclose the device inside a casing impervious to radiation. The implosion induced by the radiation would amplify the compression ... and increase the chance of the fusion bomb igniting. The key here is 'separation of the atomic charge and thermonuclear fuel, and compression of the latter by radiation travelling from the former', which constitutes 'radiation implosion'."
(This distinction between von Neumann's "ionization implosion" INSIDE the tamper, of denser tamper expanding and thus compressing lower density fusion fuel inside, and Fuchs' OUTSIDE capsule "radiation implosion", is key even today for isentropic H-bomb design; it seems Teller's key breakthroughs were not separate stages or implosion but rather radiation mirrors and ablative recoil shock compression, where radiation is used to ablate a dense pusher of Sausage designs like Mike in 1952 etc., a distinction not to be confused for the 1944 von Neumann and 1946 Fuchs implosion mechanisms! It appears Russian H-bombs used von Neumann's "ionization implosion" and Fuchs's "radiation implosion" for RDS-37 on 22 November 1955 and also in their double-primary 23 February 1958 test and subsequently, where their fusion capsules reportedly contained a BeO or other low-density outer coating, which would lead to quasi-isentropic compression, more effective for low density secondary stages than purely ablative recoil shock compression. This accounts for the continuing classification of the April 1946 Superbomb Conference (the extract of 32 pages linked here is so severely redacted that it is less helpful than the brief but very lucid summary of its technical content, in the declassified FBI compilation of reports concerning data Klaus Fuchs sent to Stalin, linked here!). Teller had all the knowledge he needed in 1946, but didn't go ahead because he made the stupid error of killing progress off by his own "no-go theorem" against compression of fusion fuel. Teller did a "theoretical" calculation in which he claimed that compression has no effect on the amount of fusion burn because the compressed system is simply scaled down in size so that the same efficiency of fusion burn occurs, albeit faster, and then stops as the fuel thermally expands. This was wrong. Teller discusses the reason for his great error in technical detail during his tape-recorded interview by Chuck Hansen at Los Alamos on 7 June 1993 (C. Hansen, Swords of Armageddon, 2nd ed., pp. II-176-7):
"Now every one of these [fusion] processes varied with the square of density. If you compress the thing, then in one unit's volume, each of the 3 important processes increased by the same factor ... Therefore, compression (seemed to be) useless. Now when ... it seemed clear that we were in trouble, then I wanted very badly to find a way out. And it occurred to be than an unprecedentedly strong compression will just not allow much energy to go into radiation. Therefore, something had to be wrong with my argument and then, you know, within minutes, I knew what must be wrong ... [energy] emission occurs when an electron and a nucleus collide. Absorption does not occur when a light quantum and a nucleus ... or ... electron collide; it occurs when a light quantum finds an electron and a nucleus together ... it does not go with the square of the density, it goes with the cube of the density." (This very costly theoretical error, wasting five years 1946-51, could have been resolved by experimental nuclear testing. There is always a risk of this in theoretical physics, which is why experiments are done to check calculations before prizes are handed out. The ban on nuclear testing is a luddite opposition to technological progress in improving deterrence.)
(This 1946-51 theoretical "no-go theorem" anti-compression error of Teller's, which was contrary to the suggestion of compression at the April 1946 superbomb conference as Teller himself refers to on 14 August 1952, and which was corrected only by comparison of the facts about compression validity in pure fission cores in Feb '51 after Ulam's argument that month for fission core compression by lens focussed primary stage shock waves, did not merely lead to Teller's dismissal of vital compression ideas. It also led to his false equations - exaggerating the cooling effect of radiation emission - causing underestimates of fusion efficiency in all theoretical calculations done of fusion until 1951! For this reason, Teller later repudiated the calculations that allegedly showed his Superbomb would fizzle; he argued that if it had been tested in 1946, the detailed data obtained - regardless of whatever happened - would have at least tested the theory which would have led to rapid progress, because the theory was wrong. The entire basis of the cooling of fusion fuel by radiation leaking out was massively exaggerated until Lawrence Livermore weaponeer John Nuckolls showed that there is a very simple solution: use baffle re-radiated, softened x-rays for isentropic compression of low-density fusion fuel, e.g. very cold 0.3 kev x-rays rather than the usual 1-10 kev cold-warm x-rays emitted directly from the fission primary. Since the radiation losses are proportional to the fourth-power of the x-ray energy or temperature, losses are virtually eliminated, allowing very efficient staging as for Nuckolls' 99.9% 10 Mt clean Ripple II, detonated on 30 October 1962 at Christmas Island. Teller's classical Superbomb was actually analyzed by John C. Solem in a 15 December 1978 report, A modern analysis of Classical Super, LA-07615, according to a Freedom of Information Act request filed by mainstream historian Alex Wellerstein, FOIA 17-00131-H, 12 June 2017; according to a list of FOIA requests at https://www.governmentattic.org/46docs/NNSAfoiaLogs_2016-2020.pdf. However, a google search for the documents Dr Wellerstein requested shows only a few at the US Gov DOE Opennet OSTI database or otherwise online yet e.g. LA-643 by Teller, On the development of Thermonuclear Bombs dated 16 Feb. 1950. The page linked here stating that report was "never classified" is mistaken! One oddity about Teller's anti-compression "no-go theorem" is that the even if fusion rates were independent of density, you would still want compression of fissile material in a secondary stage such as a radiation imploded Alarm Clock, because the whole basis of implosion fission bombs is the benefit of compression; another issue is that even if fusion rates are unaffected by density, inward compression would still help to delay the expansion of the fusion system which leads to cooling and quenching of the fusion burn.)
ABOVE: the FBI file on Klaus Fuchs contains a brief summary of the secret April 1946 Super Conference at Los Alamos which Fuchs attended, noting that compression of fusion fuel was discussed by Lansdorf during the morning session on 19 April, attended by Fuchs, and that: "Suggestions were made by various people in attendance as to the manner of minimizing the rise in entropy during compression." This fact is vitally interesting, since it proves that an effort was being made then to secure isentropic compression of low-density fusion fuel in April 1946, sixteen years before John H. Nuckolls tested the isentropically compressed Ripple II device on 30 October 1962, giving a 99.9% clean 10 megaton real H-bomb! So the Russians were given a massive head start on this isentropic compression of low-density fusion fuel for hydrogen bombs, used (according to Trutnev) in both the single primary tests like RDS-37 in November 1955 and also in the double-primary designs which were 2.5 times more efficient on a yield-to-mass basis, tested first on 23 February 1958! According to the FBI report, the key documents Fuchs gave to Russia were LA-551, Prima facie proof of the feasibility of the Super, 15 Apr 1946 and the LA-575 Report of conference on the Super, 12 June 1946. Fuchs also handed over to Russia his own secret Los Alamos reports, such as LA-325, Initiator Theory, III. Jet Formation by the Collision of Two Surfaces, 11 July 1945, Jet Formation in Cylindrical lmplosion with 16 Detonation Points, Secret, 6 February 1945, and Theory of Initiators II, Melon Seed, Secret, 6 January 1945. Note the reference to Bretscher attending the Super Conference with Fuchs; Teller in a classified 50th anniversary conference at Los Alamos on the H-bomb claimed that after he (Teller) left Los Alamos for Chicago Uni in 1946, Bretscher continued work on Teller's 31 August 1946 "Alarm Clock" nuclear weapon (precursor of the Mike sausage concept etc) at Los Alamos; it was this layered uranium and fusion fuel "Alarm Clock" concept which led to the departure of Russian H-bomb design from American H-bomb design, simply because Fuchs left Los Alamos in June 1946, well before Teller invented the Alarm Clock concept on 31 August 1946 (Teller remembered the date precisely simply because he invented the Alarm Clock on the day his daughter was born, 31 August 1946! Teller and Richtmyer also developed a variant called "Swiss Cheese", with small pockets or bubbles of expensive fusion fuels, dispersed throughout cheaper fuel, in order to kinder a more cost-effective thermonuclear reaction; this later inspired the fission and fusion boosted "spark plug" ideas in later Sausage designs; e.g. security cleared Los Alamos historian Anne Fitzpatrick stated during her 4 March 1997 interview with Robert Richtmyer, who co-invented the Alarm Clock with Teller, that the Alarm Clock evolved into the spherical secondary stage of the 6.9 megaton Castle-Union TX-14 nuclear weapon!).
In fact (see Lawrence Livermore National Laboratory nuclear warhead designer Nuckolls' explanation in report UCRL-74345): "The rates of burn, energy deposition by charged reaction products, and electron-ion heating are proportional to the density, and the inertial confinement time is proportional to the radius. ... The burn efficiency is proportional to the product of the burn rate and the inertial confinement time ...", i.e. the fusion burn rate is directly proportional to the fuel density, which in turn is of course inversely proportional to the cube of its radius. But the inertial confinement time for fusion to occur is proportional to the radius, so the fusion stage efficiency in a nuclear weapon is the product of the burn rate (i.e., 1/radius^3) and time (i.e., radius), so efficiency ~ radius/(radius^3) ~ 1/radius^2. Therefore, for a given fuel temperature, the total fusion burn, or the efficiency of the fusion stage, is inversely proportional to the square of the compressed radius of the fuel! (Those condemning Teller's theoretical errors or "arrogance" should be aware that he pushed hard all the time for experimental nuclear tests of his ideas, to check if they were correct, exactly the right thing to do scientifically and others who read his papers had the opportunity to point out any theoretical errors, but was rebuffed by those in power, who used a series of contrived arguments to deny progress, based upon what Harry would call "subconscious bias", if not arrogant, damning, overt bigotry against the kind of credible, overwhelming deterrence which had proved lacking a decade earlier, leading to WWII. This callousness towards human suffering in war and under dictatorship existed in some UK physicists too: Joseph Rotblat's hatred of anything to deter Russia be it civil defense or tactical neutron bombs of the West - he had no problem smiling and patting Russia's neutron bomb when visiting their labs during cosy groupthink deluded Pugwash campaigns for Russian-style "peaceful collaboration" - came from deep family communist convictions, since his brother was serving in the Red Army in 1944 when he alleged he heard General Groves declare that the bomb must deter Russia! Rotblat stated he left Los Alamos as a result. The actions of these groups are analogous to the "Cambridge Scientists Anti-War Group" in the 1930s. After Truman ordered a H-bomb, Bradbury at Los Alamos had to start a "Family Committee" because Teller had a whole "family" of H-bomb designs, ranging from the biggest, "Daddy", through various "Alarm Clocks", all the way down to small internally-boosted fission tactical weapons. From Teller's perspective, he wasn't putting all eggs in one basket.)
Above: declassified illustration from a January 1949 secret report by the popular physics author and Los Alamos nuclear weapons design consultant George Gamow, showing his suggestion of using x-rays from both sides of a cylindrically imploded fission device to expose two fusion capsules to x-rays to test whether compression (fusion in BeO box on right side) helps, or is unnecessary (capsule on left side). Neutron counters detect 14.1 Mev T+D neutrons using time-of-flight method (higher energy neutrons traver faster than ~1 Mev fission stage neutrons, arriving at detectors first, allowing discrimination of the neutron energy spectrum by time of arrival). It took over two years to actually fire this 225 kt shot (8 May 1951)! No wonder Teller was outraged. A few interesting reports by Teller and also Oppenheimer's secret 1949 report opposing the H bomb project as it then stood on the grounds of low damage per dollar - precisely the exact opposite of the "interpretation" the media and gormless fools will assert until the cows come home - are linked here. The most interesting is Teller's 14 August 1952 Top Secret paper debunking Hans Bethe's propaganda, by explaining that contrary to Bethe's claims, Stalin's spy Klaus Fuch had the key "radiation implosion"- see second para on p2 - secret of the H-bomb because he attended the April 1946 Superbomb Conference which was not even attended by Bethe! It was this very fact in April 1946, noted by two British attendees of the 1946 Superbomb Conference before collaboration was ended later in the year by the 1946 Atomic Energy Act, statement that led to Sir James Cladwick's secret use of "radiation implosion" for stages 2 and 3 of his triple staged H-bomb report the next month, "The Superbomb", a still secret document that inspired Penney's original Tom/Dick/Harry staged and radiation imploded H-bomb thinking, which is summarized by security cleared official historian Arnold's Britain and the H-Bomb. Teller's 24 March 1951 letter to Los Alamos director Bradbury was written just 15 days after his historic Teller-Ulam 9 March 1951 report on radiation coupling and "radiation mirrors" (i.e. plastic casing lining to re-radiate soft x-rays on to the thermonuclear stage to ablate and thus compress it), and states: "Among the tests which seem to be of importance at the present time are those concerned with boosted weapons. Another is connected vith the possibility of a heterocatalytic explosion, that is, implosion of a bomb using the energy from another, auxiliary bomb. A third concerns itself with tests on mixing during atomic explosions, which question is of particular importance in connection with the Alarm Clock."
There is more to Fuchs' influence on the UK H-bomb than I go into that paper; Chapman Pincher alleged that Fuchs was treated with special leniency at his trial and later he was given early release in 1959 because of his contributions and help with the UK H-bomb as author of the key Fuchs-von Neumann x-ray compression mechanism patent. For example, Penney visited Fuchs in June 1952 in Stafford Prison; see pp309-310 of Frank Close's 2019 book "Trinity". Close argues that Fuchs gave Penney a vital tutorial on the H-bomb mechanism during that prison visit. That wasn't the last help, either, since the UK Controller for Atomic Energy Sir Freddie Morgan wrote Penney on 9 February 1953 that Fuchs was continuing to help. Another gem: Close gives, on p396, the story of how the FBI became suspicious of Edward Teller, after finding a man of his name teaching at the NY Communist Workers School in 1941 - the wrong Edward Teller, of course - yet Teller's wife was indeed a member of the Communist-front "League of women shoppers" in Washington, DC.
Chapman Pincher, who attended the Fuchs trial, writes about Fuchs hydrogen bomb lectures to prisoners in chapter 19 of his 2014 autobiography, Dangerous to know (Biteback, London, pp217-8): "... Donald Hume ... in prison had become a close friend of Fuchs ... Hume had repaid Fuchs' friendship by organising the smuggling in of new scientific books ... Hume had a mass of notes ... I secured Fuchs's copious notes for a course of 17 lectures ... including how the H-bomb works, which he had given to his fellow prisoners ... My editor agreed to buy Hume's story so long as we could keep the papers as proof of its authenticity ... Fuchs was soon due for release ..."
Chapman Pincher wrote about this as the front page exclusive of the 11 June 1952 Daily Express, "Fuchs: New Sensation", the very month Penney visited Fuchs in prison to receive his H-bomb tutorial! UK media insisted this was evidence that UK security still wasn't really serious about deterring further nuclear spies, and the revelations finally culminated in the allegations that the MI5 chief 1956-65 Roger Hollis was a Russian fellow-traveller (Hollis was descended from Peter the Great, according to his elder brother Chris Hollis' 1958 book Along the Road to Frome) and GRU agent of influence, codenamed "Elli". Pincher's 2014 book, written aged 100, explains that former MI5 agent Peter Wright suspected Hollis was Elli after evidence collected by MI6 agent Stephen de Mowbray was reported to the Cabinet Secretary. Hollis is alleged to have deliberately fiddled his report of interviewing GRU defector Igor Gouzenko on 21 November 1945 in Canada. Gouzenko had exposed the spy and Groucho Marx lookalike Dr Alan Nunn May (photo below), and also a GRU spy in MI5 codenamed Elli, who used only duboks (dead letter boxes), but Gouzenko told Pincher that when Hollis interviewed him in 1945 he wrote up a lengthy false report claiming to discredit many statements by Gouzenko: "I could not understand how Hollis had written so much when he had asked me so little. The report was full of nonsense and lies. As [MI5 agent Patrick] Stewart read the report to me [during the 1972 investigation of Hollis], it became clear that it had been faked to destroy my credibility so that my information about the spy in MI5 called Elli could be ignored. I suspect that Hollis was Elli." (Source: Pincher, 2014, p320.) Christopher Andrew claimed Hollis couldn't have been GRU spy Elli because KGB defector Oleg Gordievsky suggested it was the KGB spy Leo Long (sub-agent of KGB spy Anthony Blunt). However, Gouzenko was GRU, not KGB like Long and Gordievsky! Gordievsky's claim that "Elli" was on the cover of Long's KGB file was debunked by KGB officer Oleg Tsarev, who found that Long's codename was actually Ralph! Another declassified Russian document, from General V. Merkulov to Stalin dated 24 Nov 1945, confirmed Elli was a GRU agent inside british intelligence, whose existence was betrayed by Gouzenko. In Chapter 30 of Dangerous to Know, Pincher related how he was given a Russian suitcase sized microfilm enlarger by 1959 Hollis spying eyewitness Michael J. Butt, doorman for secret communist meetings in London. According to Butt, Hollis delivered documents to Brigitte Kuczynski, younger sister of Klaus Fuchs' original handler, the notorious Sonia aka Ursula. Hollis allegedly provided Minox films to Brigitte discretely when walking through Hyde Park at 8pm after work. Brigitte gave her Russian made Minox film enlarger to Butt to dispose of, but he kept it in his loft as evidence. (Pincher later donated it to King's College.) Other more circumstantial evidence is that Hollis recruited the spy Philby, Hollis secured spy Blunt immunity from prosecution, Hollis cleared Fuchs in 1943, and MI5 allegedly destroyed Hollis' 1945 interrogation report on Gouzenko, to prevent the airing of the scandal that it was fake after checking it with Gouzenko in 1972.
It should be noted that the very small number of Russian GRU illegal agents in the UK and the very small communist party membership had a relatively large influence on nuclear policy via infiltration of unions which had block votes in the Labour Party, as well the indirect CND and "peace movement" lobbies saturating the popular press with anti-civil defence propaganda to make the nuclear deterrent totally incredible for any provocation short of a direct all-out countervalue attack. Under such pressure, UK Prime Minister Harold Wilson's government abolished the UK Civil Defence Corps, making the UK nuclear deterrent totally incredible against major provocations, in March 1968. While there was some opposition to Wilson, it was focussed on his profligate nationalisation policies which were undermining the economy and thus destabilizing military expenditure for national security. Peter Wright’s 1987 book Spycatcher and various other sources, including Daily Mirror editor Hugh Cudlipp's book Walking on Water, documented that on 8 May 1968, the Bank of England's director Cecil King, who was also Chairman of Daily Mirror newspapers, Mirror editor Cudlipp and the UK Ministry of Defence's anti-nuclear Chief Scientific Adviser Sir Solly Zuckerman, met at Lord Mountbatten's house in Kinnerton Street, London, to discuss a coup e'tat to overthrow Wilson and make Mountbatten the UK President, a new position. King's position, according to Cudlipp - quite correctly as revealed by the UK economic crises of the 1970s when the UK was effectively bankrupt - was that Wilson was setting the UK on the road to financial ruin and thus military decay. Zuckerman and Mountbatten refused to take part in a revolution, however Wilson's government was attacked by the Daily Mirror in a front page editorial by Cecil King two days later, on 10 May 1968, headlined "Enough is enough ... Mr Wilson and his Government have lost all credibility, all authority." According to Wilson's secretary Lady Falkender, Wilson was only told of the coup discussions in March 1976.
CND and the UK communist party alternatively tried to claim, in a contradictory way, that they were (a) too small in numbers to have any influence on politics, and (b) they were leading the country towards utopia via unilateral nuclear disarmament saturation propaganda about nuclear weapons annihilation (totally ignoring essential data on different nuclear weapon designs, yields, heights of burst, the "use" of a weapon as a deterrent to PREVENT an invasion of concentrated force, etc.) via the infiltrated BBC and most other media. Critics pointed out that Nazi Party membership in Germany was only 5% when Hitler became dictator in 1933, while in Russia there were only 200,000 Bolsheviks in September 1917, out of 125 million, i.e. 0.16%. Therefore, the whole threat of such dictatorships is a minority seizing power beyond it justifiable numbers, and controlling a majority which has different views. Traditional democracy itself is a dictatorship of the majority (via the ballot box, a popularity contest); minority-dictatorship by contrast is a dictatorship by the fanatically motivated minority by force and fear (coercion) to control the majority. The coercion tactics used by foreign dictators to control the press in free countries are well documented, but never publicised widely. Hitler put pressure on Nazi-critics in the UK "free press" via UK Government appeasers Halifax, Chamberlain and particularly the loathsome UK ambassador to Nazi Germany, Sir Neville Henderson, for example trying to censor or ridicule appeasement critics David Low, to fire Captain W. E. Johns (editor of both Flying and Popular Flying, which had huge circulations and attacked appeasement as a threat to national security in order to reduce rearmament expenditure), and to try to get Winston Churchill deselected. These were all sneaky "back door" pressure-on-publishers tactics, dressed up as efforts to "ease international tensions"! The same occurred during the Cold War, with personal attacks in Scientific American and Bulletin of the Atomic Scientists and by fellow travellers on Herman Kahn, Eugene Wigner, and others who warned we need civil defence to make a deterrent of large provocations credible in the eyes of an aggressor.
Chapman Pincher summarises the vast hypocritical Russian expenditure on anti-Western propaganda against the neutron bomb in Chapter 15, "The Neutron Bomb Offensive" of his 1985 book The Secret Offensive: "Such a device ... carries three major advantages over Hiroshima-type weapons, particularly for civilians caught up in a battle ... against the massed tanks which the Soviet Union would undoubtedly use ... by exploding these warheads some 100 feet or so above the massed tanks, the blast and fire ... would be greatly reduced ... the neutron weapon produces little radioactive fall-out so the long-term danger to civilians would be very much lower ... the weapon was of no value for attacking cities and the avoidance of damage to property can hardly be rated as of interest only to 'capitalists' ... As so often happens, the constant repetition of the lie had its effects on the gullible ... In August 1977, the [Russian] World Peace Council ... declared an international 'Week of action' against the neutron bomb. ... Under this propaganda Carter delayed his decision, in September ... a Sunday service being attended by Carter and his family on 16 October 1977 was disrupted by American demonstrators shouting slogans against the neutron bomb [see the 17 October 1977 Washington Post] ... Lawrence Eagleburger, when US Under Secretary of State for Political Affairs, remarked, 'We consider it probably that the Soviet campaign against the 'neutron bomb cost some $100 million'. ... Even the Politburo must have been surprised at the size of what it could regard as a Fifth Column in almost every country." [Unfortunately, Pincher himself had contributed to the anti-nuclear nonsense in his 1965 novel "Not with a bang" in which small amounts of radioactivity from nuclear fallout combine with medicine to exterminate humanity! The allure of anti-nuclear propaganda extends to all who which to sell "doomsday fiction", not just Russian dictators but mainstream media story tellers in the West. By contrast, Glasstone and Dolan's 1977 Effects of Nuclear Weapons doesn't even mention the neutron bomb, so there was no scientific and technical effort whatsoever by the West to make it a credible deterrent even in the minds of the public it had to protect from WWIII!]
This debunks fake news that Teller's and Ulam's 9 March 1951 report LAMS-1225 itself gave Los Alamos the Mike H-bomb design, ready for testing! Teller was proposing a series of nuclear tests of the basic principles, not 10Mt Ivy-Mike which was based on a report the next month by Teller alone, LA-1230, "The Sausage: a New Thermonuclear System". When you figure that, what did Ulam actually contribute to the hydrogen bomb? Nothing about implosion, compression or separate stages - all already done by von Neumann and Fuchs five years earlier - and just a lot of drivel about trying to channel material shock waves from a primary to compress another fissile core, a real dead end. What Ulam did was to kick Teller out of his self-imposed mental objection to compression devices. Everything else was Teller's; the radiation mirrors, the Sausage with its outer ablation pusher and its inner spark plug. Note also that contrary to official historian Arnold's book (which claims due to a misleading statement by Dr Corner that all the original 1946 UK copies of Superbomb Conference documentation were destroyed after being sent from AWRE Aldermaston to London between 1955-63), all the documents did exist in the AWRE TPN (theoretical physics notes, 100% of which have been perserved) and are at the UK National Archives, e.g. AWRE-TPN 5/54 is listed in National Archives discovery catalogue ref ES 10/5: "Miscellaneous super bomb notes by Klaus Fuchs", see also the 1954 report AWRE-TPN 6/54, "Implosion super bomb: substitution of U235 for plutonium" ES 10/6, the 1954 report AWRE-TPN 39/54 is "Development of the American thermonuclear bomb: implosion super bomb" ES 10/39, see also ES 10/21 "Collected notes on Fermi's super bomb lectures", ES 10/51 "Revised reconstruction of the development of the American thermonuclear bombs", ES 1/548 and ES 1/461 "Superbomb Papers", etc. Many reports are secret and retained, despite containing "obsolete" designs (although UK report titles are generally unredacted, such as: "Storage of 6kg Delta (Phase) -Plutonium Red Beard (tactical bomb) cores in ships")! It should also be noted that the Livermore Laboatory's 1958 TUBA spherical secondary with an oralloy (enriched U235) outer pusher was just a reversion from Teller's 1951 core spark plug idea in the middle of the fusion fuel, back to the 1944 von Neumann scheme of having fission material surrounding the fusion fuel. In other words, the TUBA was just a radiation and ionization imploded, internally fusion-boosted, second fission stage which could have been accomplished a decade earlier if the will existed, when all of the relevant ideas were already known. The declassified UK spherical secondary-stage alternatives linked here (tested as Grapple X, Y and Z with varying yields but similar size, since all used the 5 ft diameter Blue Danube drop casing) clearly show that a far more efficient fusion burn occurs by minimising the mass of hard-to-compress U235 (oralloy) sparkplug/pusher, but maximising the amount of lithium-7, not lithium-6. Such a secondary with minimal fissionable material also automatically has minimal neutron ABM vulnerability (i.e., "Radiation Immunity", RI). This is the current cheap Russian neutron weapon design, but not the current Western design of warheads like the W78, W88 and bomb B61.
So why on earth doesn't the West take the cheap efficient option of cutting expensive oralloy and maximising cheap natural (mostly lithium-7) LiD in the secondary? Even Glasstone's 1957 Effects of Nuclear Weapons on p17 (para 1.55) states that "Weight for weight ... fusion of deuterium nuclei would produce nearly 3 times as much energy as the fission of uranium or plutonium"! The sad answer is "density"! Natural LiD (containing 7.42% Li6 abundance) is a low density white/grey crystalline solid like salt that actually floats on water (lithium deuteroxide would be formed on exposure to water), since its density is just 820 kg/m^3. Since the ratio of mass of Li6D to Li7D is 8/9, it would be expected that the density of highly enriched 95% Li6D is 739 kg/m^3, while for 36% enriched Li6D it is 793 kg/m^3. Uranium metal has a density of 19,000 kg/m^3, i.e. 25.7 times greater than 95% enriched li6D or 24 times greater than 36% enriched Li6D. Compactness, i.e. volume is more important in a Western MIRV warhead than mass/weight! In the West, it's best to have a tiny-volume, very heavy, very expensive warhead. In Russia, cheapness outweights volume considerations. The Russians in some cases simply allowed their more bulky warheads to protrude from the missile bus (see photo below), or compensated for lower yields at the same volume using clean LiD by using the savings in costs to build more warheads. (The West doubles the fission yield/mass ratio of some warheads by using U235/oralloy pushers in place of U238, which suffers from the problem that about half the neutrons it interacts with result in non-fission capture, as explained below. Note that the 720 kiloton UK nuclear test Orange Herald device contained a hollow shell of 117 kg of U235 surrounded by a what Lorna Arnold's book quotes John Corner referring to a "very thin" layer of high explosive, and was compact, unboosted - the boosted failed to work - and gave 6.2 kt/kg of U235, whereas the first version of the 2-stage W47 Polaris warhead contained 60 kg of U235 which produced most of the secondary stage yield of about 400 kt, i.e. 6.7 kt/kg of U235. Little difference - but because perhaps 50% of the total yield of the W47 was fusion, its efficiency of use of U235 must have actually been less than the Orange Herald device, around 3 kt/kg of U235 which indicates design efficiency limits to "hydrogen bombs"! Yet anti-nuclear charlatans claimed that the Orange Herald bomb was a con!)
ABOVE: USA nuclear weapons data declassified by UK Government in 2010 (the information was originally acquired due to the 1958 UK-USA Act for Cooperation on the Uses of Atomic Energy for Mutual Defense Purposes, in exchange for UK nuclear weapons data) as published at http://nuclear-weapons.info/images/tna-ab16-4675p63.jpg. This single table summarizes all key tactical and strategic nuclear weapons secret results from 1950s testing! (In order to analyze the warhead pusher thicknesses and very basic schematics from this table it is necessary to supplement it with the 1950s warhead design data declassified in other documents, particularly some of the data from Tom Ramos and Chuck Hansen, as quoted in some detail below.) The data on the mass of special nuclear materials in each of the different weapons argues strongly that the entire load of Pu239 and U235 in the 1.1 megaton B28 was in the primary stage, so that weapon could not have had a fissile spark plug in the centre let alone a fissile ablator (unlike Teller's Sausage design of 1951), and so the B28 it appears had no need whatsoever of a beryllium neutron radiation shield to prevent pre-initiation of the secondary stage prior to its compression (on the contrary, such neutron exposure of the lithium deuteride in the secondary stage would be VITAL to produce some tritium in it prior to compression, to spark fusion when it was compressed). Arnold's book indeed explains that UK AWE physicists found the B28 to be an excellent, highly optimised, cheap design, unlike the later W47 which was extremely costly. The masses of U235 and Li6 in the W47 shows the difficulties of trying to maintain efficiency while scaling down the mass of a two-stage warhead for SLBM delivery: much larger quantities of Li6 and U235 must be used to achieve a LOWER yield! To achieve thermonuclear warheads of low mass at sub-megaton yields, both the outer bomb casing and the pusher around the the fusion fuel must be reduced:
"York ... studied the Los Alamos tests in Castle and noted most of the weight in thermonuclear devices was in their massive cases. Get rid of the case .... On June 12, 1953, York had presented a novel concept ... It radically altered the way radiative transport was used to ignite a secondary - and his concept did not require a weighty case ... they had taken the Teller-Ulam concept and turned it on its head ... the collapse time for the new device - that is, the amount of time it took for an atomic blast to compress the secondary - was favorable compared to older ones tested in Castle. Brown ... gave a female name to the new device, calling it the Linda." - Dr Tom Ramos (Lawrence Livermore National Laboratory nuclear weapon designer), From Berkeley to Berlin: How the Rad Lab Helped Avert Nuclear War, Naval Institute press, 2022, pp137-8. (So if you reduce the outer casing thickness to reduce warhead weight, you must complete the pusher ablation/compression faster, before the thinner outer casing is blown off, and stops reflecting/channelling x-rays on the secondary stage. Making the radiation channel smaller and ablative pusher thinner helps to speed up the process. Because the ablative pusher is thinner, there is relatively less blown-off debris to block the narrower radiation channel before the burn ends.)
"Brown's third warhead, the Flute, brought the Linda concept down to a smaller size. The Linda had done away with a lot of material in a standard thermonuclear warhead. Now the Flute tested how well designers could take the Linda's conceptual design to substantially reduce not only the weight but also the size of a thermonuclear warhead. ... The Flute's small size - it was the smallest thermonuclear device yet tested - became an incentive to improve codes. Characteristics marginally important in a larger device were now crucially important. For instance, the reduced size of the Flute's radiation channel could cause it to close early [with ablation blow-off debris], which would prematurely shut off the radiation flow. The code had to accurately predict if such a disaster would occur before the device was even tested ... the calculations showed changes had to be made from the Linda's design for the Flute to perform correctly." - Dr Tom Ramos (Lawrence Livermore National Laboratory nuclear weapon designer), From Berkeley to Berlin: How the Rad Lab Helped Avert Nuclear War, Naval Institute press, 2022, pp153-4. Note that the piccolo (the W47 secondary) is a half-sized flute, so it appears that the W47's secondary stage design miniaturization history was: Linda -> Flute -> Piccolo:
"A Division's third challenge was a small thermonuclear warhead for Polaris [the nuclear SLBM submarine that preceeded today's Trident system]. The starting point was the Flute, that revolutionary secondary that had performed so well the previous year. Its successor was called the Piccolo. For Plumbbob [Nevada, 1957], the design team tested three variations of the Piccolo as a parameter test. One of the variants outperformed the others ... which set the stage for the Hardtack [Nevada and Pacific, 1958] tests. Three additional variations for the Piccolo ... were tested then, and again an optimum candidate was selected. ... Human intuition as well as computer calculations played crucial roles ... Finally, a revolutionary device was completed and tested ... the Navy now had a viable warhead for its Polaris missile. From the time Brown gave Haussmann the assignment to develop this secondary until the time they tested the device in the Pacific, only 90 days had passed. As a parallel to the Robin atomic device, this secondary for Polaris laid the foundation for modern thermonuclear weapons in the United States." - Dr Tom Ramos (Lawrence Livermore National Laboratory nuclear weapon designer), From Berkeley to Berlin: How the Rad Lab Helped Avert Nuclear War, Naval Institute press, 2022, pp177-8. (Ramos is very useful in explaining that many of the 1950s weapons with complex non-spherical, non-cylindrical shaped primaries and secondaries were simply far too complex to fully simulate on the really pathetic computers they had - Livermore got a 4,000 vacuum tubes-based IBM 701 with 2 kB memory in 1956, AWRE Aldermaston in the Uk had to wait another year for theirs - so they instead did huge numbers of experimental explosive tests. For instance, on p173, Ramos discloses that the Swan primary which developed into the 155mm tactical shell, "went through over 100 hydrotests", non-nuclear tests in which fissile material is replaced with U238 or other substitutes, and the implosion is filmed with flash x-ray camera systems.)
"An integral feature of the W47, from the very start of the program, was the use of an enriched uranium-235 pusher around the cylindrical secondary." - Chuck Hansen, Swords 2.0, p. VI-375 (Hansen's source is his own notes taken during a 19-21 February 1992 nuclear weapons history conference he attended; if you remember the context, "Nuclear Glasnost" became fashionable after the Cold War ended, enabling Hansen to acquire almost unredacted historical materials for a few years until nuclear proliferation became a concern in Iraq, Afghanistan, Iran and North Korea). The key test of the original (Robin primary and Piccolo secondary) Livermore W47 was 412 kt Hardtack-Redwood on 28 June 1958. Since Li6D utilized at 100% efficiency would yield 66 kt/kg, the W47 fusion efficiency was only about 6%; since 100% fission of u235 yields 17 kt/kg, the W47's Piccolo fission (the u235 pusher) efficiency was about 20%; the comparable figures for secondary stage fission and fusion fuel burn efficiencies in the heavy B28 are about 7% and 15%, respectively:
ABOVE: the heavy B28 gave a very "big bang for the buck": it was cheap in terms of expensive Pu, U235 and Li6, and this was the sort of deterrent which was wanted by General LeMay for the USAF, which wanted as many weapons as possible, within the context of Eisenhower's budgetary concerns. But its weight (not its physical size) made it unsuitable for SLBM Polaris warheads. The first SLBM warhead, the W47, was almost the same size as the B28 weapon package, but much lighter due to having a much thinner "pusher" on the secondary, and casing. But this came at a large financial cost in terms of the quantities of special nuclear materials required to get such a lightweight design to work, and also a large loss of total yield. The fusion fuel burn efficiency ranges from 6% for the 400 kt W47 to 15% for the 1.1 megaton B28 (note that for very heavy cased 11-15 megaton yield tests at Castle, up to 40% fusion fuel burn efficiency was achieved), whereas the secondary stage ablative pusher fission efficiency ranged from 7% for a 1.1 inch thick natural uranium (99.3% U238) ablator to 20% for a 0.15 inch thick highly enriched oralloy (U235) ablator. From the brief description of the design evolution given by Dr Tom Ramos (Lawrence Livermore National Laboratory), it appears that when the x-ray channelling outer case thickness of the weapon is reduced to save weight, the duration of the x-ray coupling is reduced, so the dense metal pusher thickness must be reduced if the same compression factor (approximately 20) for the secondary stage is to be accomplished (lithium deuteride, being of low density, is far more compressable by a given pressure, than dense metal). In both examples, the secondary stage is physically a boosted fission stage. (If you are wondering why the hell the designers don't simply use a hollow core U235 bomb like Orange Herald instead of bothering with such inefficient x-ray coupled two-stage designs as these, the answer is straightforward: the risk of large fissile core meltdown by neutrons Moscow ABM defensive nuclear warheads, neutron bombs.)
The overall weight of the W47 was minimized by replacing the usual thick layer of U238 pusher with a very thin layer of fissile U235 (supposedly Teller's suggestion), which is more efficient for fission, but is limited by critical mass issues. The W47 used a 95% enriched Li6D cylinder with a 3.8mm thick U235 pusher; the B28 secondary was 36% enriched Li6D, with a very heavy 3cm thick U238 pusher. As shown below, it appears the B28 was related to the Los Alamos clean design of the TX21C tested as 95% clean 4.5 megatons Redwing-Navajo in 1956 and did not have a central fissile spark plug. From the declassified fallout composition, it is known the Los Alamos designers replaced the outer U238 pusher of Castle secondaries with lead in Navajo. Livermore did the same for their 85% clean 3.53 megatons Redwing-Zuni test, but Livermore left the central fission spark plug, which contributed 10% of its 15% fission yield, instead of removing the neutron shield, using foam channel filler for slowing down the x-ray compression, and thereby using primary stage neutrons to split lithium-6 giving tritium prior to compression. Our point is that Los Alamos got it wrong in sticking too conservatively to ideology: for clean weapons they should have got rid of the dense lead pusher and gone for John H. Nuckolls idea (also used by Fuchs in 1946 and the Russians in 1955 and 1958) of a low-density pusher for isentropic compression of low-density fusion fuel. This error is the reason why those early cleaner weapons were extremely heavy due to unnecessary 2" thick lead or tungsten pushers around the fusion fuel, which massively reduced their yield-to-weight ratios, so that LeMay rejected them!
Compare these data for the 20 inch diameter, 49 inch, 1600 lb, 1.1 megaton bomb B28 to the 18 inch diameter, 47 inch, 700 lb, 400 kt Mk47/W47 Polaris SLBM warhead (this is the correct yield for the first version of the W47 confirmed by UK data in Lorna Arnold Britain and the H-bomb 2001 and AB 16/3240; Wikipedia wrongly gives the 600 kt figure in Hansen, which was a speculation or a later upgrade). The key difference is that the W47 is much lighter, and thus suitable for the Polaris SLBM unlike the heavier, higher yield B28. Both B28 and W47 used cylindrical sausages, but they are very different in composition; the B28 used a huge mass of U238 in its ablative sausage outer shell or pusher, while the W47 used oralloy/U235 in the pusher. The table shows the total amounts of Pu, Oralloy (U235), Lithium-6 (excluding cheaper lithium-7, which is also present in varying amounts in different thermonuclear weapons), and tritium (which is used for boosting inside fissile material, essentially to reduce the amount of Pu and therefore the vulnerability of the weapon to Russian enhanced neutron ABM warhead meltdown). The B28 also has an external dense natural U (99.3% U238) "ablative pusher shell" whose mass is not listed in this table. The table shows that the 400 kt W47 Polaris SLBM warhead contains 60 kg of U235 (nearly as much as the 500 kt pure fission Mk18), which is in an ablative pusher shell around the lithium deuteride, so that the cylinder of neutron-absorbing lithium-6 deuteride within it keeps that mass of U235 subcritical, until compressed. So the 400 kt W47 contains far more Pu, U235, Li6 and T than the higher yield 1.1 megaton B28: this is the big $ price you pay for reducing the mass of the warhead; the total mass of the W47 is reduced to 44% of the mass of the B28, since the huge mass of cheap U238 pusher in the B28 is replaced by a smaller mass of U235, which is more efficient because (as Dr Carl F. Miller reveals in USNRDL-466, Table 6), about half of the neutrons hitting U238 don't cause fission but instead non-fission capture reactions which produce U239, plus the n,2n reaction that produces U237, emitting a lot of very low energy gamma rays in the fallout. For example, in the 1954 Romeo nuclear test (which, for simplicity, we quote since it used entirely natural LiD, with no expensive enrichment of the Li6 isotope whatsoever), the U238 jacket fission efficiency was reduced by capture as follows: 0.66 atom/fission of U239, 0.10 atom/fission of U237 and 0.23 atom/fission of U240 produced by fission, a total of 0.66 + 0.10 + 0.23 ~ 1 atom/fission, i.e. 50% fission in the U238 pusher, versus 50% non-fission neutron captures. So by using U235 in place of U238, you virtually eliminate the non-fission capture (see UK Atomic Weapons Establishment graph of fission and capture cross-sections for U235, shown below), which roughly halves the mass of the warhead, for a given fission yield. This same principle of using an outer U235/oralloy pusher instead of U238 to reduce mass - albeit with the secondary cylindrical "Sausage" shape now changed to a sphere - applies to today's miniaturised, high yield, low mass "MIRV" warheads. Just as the lower-yield W47 counter-intuitively used more expensive ingredients than the bulkier higher-yield B28, modern compact, high-yield oralloy-loaded warheads literally cost a bomb, just to keep the mass down! There is evidence Russia uses alternative ideas.
This is justified by the data given for a total U238 capture-to-fission ratio of 1 in the 11 megaton Romeo test and also the cross-sections for U235 capture and fission on the AWE graph for relevant neutron energy range of about 1-14 Mev. If half the neutrons are captured in U238 without fission, then the maximum fission yield you can possibly get from "x" kg of U238 pusher is HALF the energy obtained from 100% fission of "x" kg of U238. Since with U238 only about half the atoms can undergo fission by thermonuclear neutrons (because the other half undergo non-fission capture), the energy density (i.e., the Joules/kg produced by the fission explosion of the pusher) reached by an exploding U238 pusher is only half that reached by U235 (in which there is less non-fission capture of neutrons, which doubles the pusher mass without doubling the fission energy release). So a U235 pusher will reach twice the temperature of a U238 pusher, doubling its material heating of fusion fuel within, prolonging the fusion burn and thus increasing fusion burn efficiency. 10 MeV neutron energy is important since it allows for likely average scattering of 14.1 MeV D+T fusion neutrons and it is also the energy at which the most important capture reaction, the (n,2n) cross-section peaks for both U235 (peak of 0.88 barn at 10 Mev) and U238 (peak of 1.4 barns at 10 Mev). For 10 Mev neutrons, U235 and U238 have fission cross-sections of 1.8 and 1 barn, respectively. For 14 Mev neutrons, U238 has a (n,2n) cross section of 0.97 barn for U237 production. So ignoring non-fission captures, you need 1.8/1 = 1.8 times greater thickness of pusher for U238 than for U235, to achieve the same amount of fission. But this simple consideration ignores the x-ray ablation requirement of the explosing pusher, so there are several factors requiring detailed computer calculations, and/or nuclear testing.
Note: there is an extensive collection of declassified documents released after Chuck Hansen's final edition, Swords 2.0, which are now available at https://web.archive.org/web/*/http://www.nnsa.energy.gov/sites/default/files/nnsa/foiareadingroom/*, being an internet-archive back-up of a now-removed US Government Freedom of Information Act Reading Room. Unfortunately they were only identified by number sequence, not by report title or content, in that reeding room, and so failed to achieve wide attention when originally released! (This includes extensive "Family Committee" H-bomb documentation and many long-delayed FOIA requests submitted originally by Hansen, but not released in time for inclusion in Swords 2.0.) As the extract below - from declassified document RR00132 - shows, some declassified documents contained very detailed information or typewriter spaces that could only be filled by a single specific secret word (in this example, details of the W48 linear implosion tactical nuclear warhead, including the fact that it used PBX9404 plastic bonded explosive glued to the brittle beryllium neutron reflector around the plutonium core using Adiprene L100 adhesive!).
ABOVE: Declassified data on the radiation flow analysis for the 10 megaton Mike sausage: http://nnsa.energy.gov/sites/default/files/nnsa/foiareadingroom/RR00198.pdf
Note that the simplistic "no-go theorem" given in this extract, against any effect from varying the temperature to help the radiation channelling, was later proved false by John H. Nuckolls (like Teller's anti-compression "no-go theorem" was later proved false), since lowered temperature delivers energy where it is needed while massively reducing radiation losses (which go as the fourth power of temperature/ x-ray energy in kev).
ABOVE: Hans A. Bethe's disastrous back-of-the-envelope nonsense "non-go theorem" against lithium-7 fission into tritium by 14.1 Mev D+T neutrons in Bravo (which contained 40% lithium-6 and 60% lithium-7; unnecessarily enriched - at great expense and effort - from the natural 7.42% lithum-6 abundance). It was Bethe's nonsense "physics" speculation, unbacked by serious calculation, who caused Bravo to go off at 2.5 times the expected 6 megatons and therefore for the Japanese Lucky Dragon tuna trawler crew in the maximum fallout hotspot area 80 miles downwind to be contaminated by fallout, and also for Rongelap's people to be contaminated ("accidents" that inevitably kickstarted the originally limited early 1950s USSR funded Communist Party anti-nuclear deterrence movements in the West into mainstream media and thus politics). There was simply no solid basis for assuming that the highly penetrating 14.1 Mev neutrons would be significantly slowed by scattering in the fuel before hitting lithium-7 nuclei. Even teller's 1950 report LA-643 at page 17 estimated that in a fission-fusion Alarm Clock, the ratio of 14 Mev to 2.5 Mev neutrons was 0.7/0.2 = 3.5. Bethe's complacently bad guesswork-based physics also led to the EMP fiasco for high altitude bursts, after he failed to predict the geomagnetic field deflection of Compton electrons at high altitude in his secret report “Electromagnetic Signal Expected from High-Altitude Test”, Los Alamos report LA-2173, October 1957, Secret. He repeatedly caused nuclear weapons effects study disasters. For the true utility of lithium-7, which is actually BETTER than lithum-6 at tritium production when struck by 14.1 Mev D+T fusion neutrons, and its consequences for cheap isentropically compressed fusion capsules in Russian neutron bombs, please see my paper here which gives a graph of lithium isotopic cross section versus neutron energy, plus the results when Britain used cheap lithium-7 in Grapple Y to yield 3 megatons (having got lower yields with costly lithium-6 in previous tests!).
Above: Edward Leader-Williams on the basis for UK civil defence shelters in SECRET 1949 Royal Society's London Symposium on physical effects of atomic weapons, a study that was kept secret by the Attlee Government and subsequent UK governments, instead of being openly published to enhance public knowledge of civil defence effectiveness against nuclear attack. Leader-Williams also produced the vital civil defence report seven years later (published below for the first time on this blog), proving civil defence sheltering and city centre evacuation is effective against 20 megaton thermonuclear weapons. Also published in the same secret symposium, which was introduced by Penney, was Penney's own Hiroshima visit analysis of the percentage volume reduction in overpressure-crushed empty petrol cans, blueprint containers, etc., which gave a blast partition yield of 7 kilotons (or 15.6 kt total yield, if taking the nuclear blast as 45% of total yield, i.e. 7/0.45 = 15.6, as done in later AWRE nuclear weapons test blast data reports). Penney in a 1970 updated paper allowed for blast reduction due to the damage done in the city bursts.
Russian propagandists are discussing the best way to scare the West - testing a nuclear Tsar Bomb or checking bomb shelters. pic.twitter.com/qWCaxjvfM8
— TheKremlinYap (@TheKremlinYap) October 4, 2023
Nuclear saber-rattling from Russian propagandists. They think tactical nuclear weapons aren't enough, and strategic ones should be used.
Russia has been very active with its nuclear rhetoric recently. pic.twitter.com/1glutLoeqV
— Anton Gerashchenko (@Gerashchenko_en) September 29, 2023
Review of Peter Kuran's excellent "Neutron Bomb Movie".
Below is a brief clip for review purposes from a longer newsreel of President Eisenhower, enthusiastically promoting the 96% clean fusion Poplar nuclear test (detonated 12 July 1958). On 30 October 1962, Kennedy tested… pic.twitter.com/y4QpR5eCum
— nukegate.org (@Nukegate) September 29, 2023
Attention, Great Britain!
Threats to blow up British nuclear facilities from a Russian propagandist. pic.twitter.com/VGX4pjSz8A
— Anton Gerashchenko (@Gerashchenko_en) September 13, 2023
ABOVE: The British government has now declassified detailed summary reports giving secret original nuclear test data on the EMP (electromagnetic pulse) damage due to numerous nuclear weapons, data which is still being kept under wraps in America since it hasn't been superseded because Western atmospheric nuclear tests were stopped late in 1962 and never resumed - even though the Russians have even more extensive data - completely debunking Glasstone and Dolan's disarmament propaganda nonsense in the 1962, 1964 and 1977 Effects of Nuclear Weapons which ignores EMP piped far away from low altitude nuclear tests by power and communications cables and falsely claims instead that such detonations don't produce EMP damage outside the 2psi blast radius! For a discussion of the new data and also a link to the full 200+ pages version (in addition to useful data, inevitably like all official reports it also contains a lot of "fluff" padding), please see the other (physics) site: https://nige.wordpress.com/2023/09/12/secret-emp-effects-of-american-nuclear-tests-finally-declassified-by-the-uk-and-at-uk-national-archives/ (by contrast, this "blogspot" uses old non-smartphone proof coding, no longer properly indexed any long longer by "google's smartphone bot"). BELOW: declassified British nuclear war planning blast survival data showing that even without special Morrison table shelters, the American assumption that nobody can survive in a demolished house is false, based on detailed WWII British data (the majority of people in houses flattened within 77 ft from V1 Nazi cruise missiles survived!), and secret American reports (contradicting their unclassified propaganda) proved that blast survival occurred at 16 psi overpressure in Hiroshima's houses, e.g. see limited distribution Dirkwood corp DC-P-1060 for Hiroshima, also the secret 1972 Capabilities of Nuclear Weapons DNA-EM-1 table 10-1, and WWII report RC-450 table 8.2, p145 (for determining survival of people sheltered in brick houses, the WWII A, B, C, and D damage versus casualty data from V1 blast was correlated to similar damage from nuclear blast as given Glasstone's 1957 Effects of Nuclear Weapons page 249, Fig. 6.41a, and page 109 Fig. 3.94a, which show that A, B, C, and D damage to brick houses from nuclear weapons occur at peak overpressures of 9, 6, 3 and 0.5 psi, respectively; the longer blast from higher yields blows the debris over a wider area, reducing the load per unit area falling on to people sheltered under tables etc), and the declassified UK government assessment of nuclear terrorist attack on a port or harbour, as well as the confidential classified UK Government analysis of the economic and social effects from WWII bombing (e.g. the recovery times for areas as a function of percentage of houses destroyed):
Note: the DELFIC, SIMFIC and other computer predicted fallout area comparisons for the 110 kt Bikini Atoll Castle-Koon land surface burst nuclear test are false since the distance scale of Bikini Atoll is massively exaggerated on many maps, e.g. in the Secret January 1955 AFSWP "Fall-out Symposium", the Castle fallout report WT-915, and the fallout patterns compendium DASA-1251! The Western side of the Bikini Atoll reef is at 165.2 degrees East, while the most eastern island in the Bikini Atoll, Enyu, is at 165.567 degrees East: since there are 60 nautical miles per degree by definition, the width of Bikini Atoll is therefore (165.567-165.2)(60) = 22 nautical miles, approximately half the distance shown in the Castle-Koon fallout patterns. Since area is proportional to the square of the distance scale, this constitutes a serious exaggeration in fallout casualty calculations, before you get into the issue of the low energy (0.1-0.2 MeV) gamma rays from neutron induced Np239 and U237 in the fallout enhancing the protection factor of shelters (usually calculated assuming hard 1.17 and 1.33 MeV gamma rads from Co60), during the sheltering period of approximately 1-14 days after detonation.
Unofficial Russian video on the secret Russian nuclear shelters from Russian Urban Exploration, titled "Проникли на секретный Спецобъект Метро!" = "We infiltrated a secret special facility of the Metro!":
ABOVE: Moscow Metro and Metro-2 (secret nuclear subway) horizonially swinging blast doors take only 70 seconds to shut, whereas their vertically rising blast doors take 160 seconds to shut; both times are however far shorter than the arrival time of Western ICBMs or even SLBMs which take 15-30 minutes by which time the Russian shelters are sealed from blast and radiation! In times of nuclear crisis, Russia planned to evacuate from cities those who could not be sheltered, and for the remainder to be based in shelters (similarly to the WWII British situation, when people slept in shelters of one kind or another when there was a large risk of being bombed without notice, particularly in supersonic V2 missile attacks where little warning time was available).

(For the essential so-called "overkill" background or Sir Slim's "the more you use, fewer you lose" success formula for winning in Burma against Japan - where physicist Herman Kahn served while his friend Sam Cohen was calculating nuclear weapon efficiencies at the Los Alamos Manhattan Project, which again used "overkill" to convince the opponent to throw in the towel - please see my post on the practicalities of really DETERRING WWIII linked here.)
ABOVE: Russian 1985 1st Cold War SLBM first strike plan. The initial use of Russian SLBM launched nuclear missiles from off-coast against command and control centres (i.e. nuclear explosions to destroy warning satellite communications centres by radiation on satellites as well as EMP against ground targets, rather than missiles launched from Russia against cities, as assumed by 100% of the Cold War left-wing propaganda) is allegedly a Russian "fog of war" strategy. Such a "demonstration strike" is aimed essentially at causing confusion about what is going on, who is responsible - it is not quick or easy to finger-print high altitude bursts fired by SLBM's from submerged submarines to a particular country because you don't get fallout samples to identify isotopic plutonium composition. Russia could immediately deny the attack (implying, probably to the applause of the left-wingers that this was some kind of American training exercise or computer based nuclear weapons "accident", similar to those depicted in numerous anti-nuclear Cold War propaganda films). Thinly-veiled ultimatums and blackmail follow. America would not lose its population or even key cities in such a first strike (contrary to left-wing propaganda fiction), as with Pearl Harbor in 1941; it would lose its complacency and its sense of security through isolationism, and would either be forced into a humiliating defeat or a major war.
Before 1941, many warned of the risks but were dismissed on the basis that Japan was a smaller country with a smaller economy than the USA and war was therefore absurd (similar to the way Churchill's warnings about European dictators were dismissed by "arms-race opposing pacifists" not only in the 1930s, but even before WWI; for example Professor Cyril Joad documents in the 1939 book "Why War?" his first hand witnessing of Winston Churchill's pre-WWI warning and call for an arms-race to deter that war by the sneering Norman Angell). It is vital to note that there is an immense pressure against warnings of Russian nuclear superiority even today, most of it contradictory. E.g. the left wing (Russian biased) "experts" whose voices are the only ones reported in the Western media (traditionally led by "Scientific American" and "Bulletin of the Atomic Scientists"), simultaneously claim Russia imposes such a complex SLBM and ICBM threat that we must disarm now, while also claiming that their tactical nuclear weapons probably won't work so aren't a threat! In similar vein, Teller-critic Hans Bethe also used to falsely "dismiss" Russian nuclear superiority by claiming (with any more evidence than Brezhnev's word, it appeared) that Russian delivery systems are "less accurate" than Western missiles (as if accuracy has anything to do with high altitude EMP strikes, where the effects cover thousands of miles radii). Such claims would then by repeatedly endlessly in the Western media by Russian biased "journalists" or agents of influence, and any attempt to point out the propaganda would turn into a "Reds under beds" argument, designed to imply that the truth is dangerous to "peaceful coexistence"!
The Top Secret American intelligency report NIE 11-3/8-74 "Soviet Forces for Intercontinental Conflict" warned on page 6: "the USSR has largely eliminated previous US quantitative advantages in strategic offensive forces." page 9 of the report estimated that the Russian's ICBM and SLBM launchers exceed the USAs 1,700 during 1970, while Russia's on-line missile throw weight had exceeded the USA's one thousand tons back in 1967! Because the USA had more long-range bombers which can carry high-yield bombs than Russia (bombers are more vulnerable to air defences so were not Russia's priority), it took a little longer for Russia to exceed the USA in equivalent megatons, but the 1976 Top Secret American report NIE 11-3/8-76 at page 17 shows that in 1974 Russia exceeded the 4,000 equivalent-megatons payload of USA missiles and aircraft (with less vulnerability for Russia, since most of Russia's nuclear weapons were on missiles not in SAM-vulnerable aircraft), amd by 1976 Russia could deliver 7,000 tons of payload by missiles compared to just 4,000 tons on the USA side. These reports were kept secret for decades to protect the intelligence sources, but they were based on hard evidence. For example, in August 1974 the Hughes Aircraft Company used a specially designed ship (Glomar Explorer, 618 feet long, developed under a secret CIA contract) to recover nuclear weapons and their secret manuals from a Russian submarine which sank in 16,000 feet of water, while in 1976 America was able to take apart the electronics systems in a state-of-the-art Russian MIG-25 fighter which was flown to Japan by defector Viktor Belenko, discovering that it used exclusively EMP-hard miniature vacuum tubes with no EMP-vulnerable solid state components.
Update: Lawrence Livermore National Laboratory's $3.5 billion National Ignition Facility, NIF, using ultraviolet wavelength laser beam pulses of 2MJ on to a 2mm diameter spherical beryllium shell of frozen D+T inside a 1 cm-long hollow gold cylinder "hohlraum" (which is heated to a temperature where it then re-radiates energy at much higher frequency, x-rays, on to the surface of the beryllium ablator of the central fusion capsule, which ablates causing it to recoil inward (as for the 1962 Ripple II nuclear weapon's secondary stage, the capsule is compressed by a factor of 35, mimicking the isentropic compression mechanism of a miniature Ripple II clean nuclear weapon secondary stage), has now repeatedly achieved nuclear fusion explosions of over 3MJ, equivalent to nearly 1 kg of TNT explosive. According to a Time article (linked her) about fusion system designer Annie Kritcher, the recent breakthrough was in part due to using a ramping input energy waveform: "success that came thanks to tweaks including shifting more of the input energy to the later part of the laser shot", a feature that minimises the rise in entropy due to shock shock wave generation (which heats the capsule, causing it to expand and resist compression) and increases isentropic compression which was the principle used by LLNL's J. H. Nuckolls to achieve the 99.9% clean Ripple II 9.96 megaton nuclear test success in Dominic-Housatonic on 30 October 1962. Nuckolls in 1972 published the equation for the idealized input power waveform required for isentropic, optimized compression of fusion fuel (Nature, v239, p139): P ~ (1 - t)-1.875, where t is time in units of the transit time (the time taken for the shock to travel to the centre of the fusion capsule), and -1.875 a constant based on the specific heat of the ionized fuel (Nuckolls has provided the basic declassified principles, see extract linked here).
In a fission primary, speed of compression is of the essence in order to beat pre-initiation (where a stray spontaneous fission neutron from Pu-240 or Pu-242 impurities sets off the chain reaction before maximum compression is obtained, reducing the yield). But this danger is not possible when compressing a 100% fusion capsule, where speed is not the key, and fusion is automatically initiated when the compression squeezes the D+T to an adequate density. Provided that the compression mechanism is efficient for fusion, time is not of the essence. The fusion burn efficiency is a function of the compression attained, rather than the speed of implosion. To be clear, the energy reliably released by the 2mm diameter capsule of fusion fuel was roughly a 1 kg TNT explosion. 80% of this is in the form of 14.1 MeV neutrons (ideal for fissioning lithium-7 in LiD to yield more tritium), and 20% is the kinetic energy of fused nuclei (which is quickly converted into x-rays radiation energy by collisions). If this neutron and x-ray energy can be coupled by a scattering container into a small second stage of Li6D, it will be possible to set off a multiplicative chain reaction of fusion capsule stages, rapidly increasing the total fusion energy release. Nuckolls' 9.96 megaton Housatonic (10 kt Kinglet primary and 9.95 Mt Ripple II 100% clean isentropically compressed secondary) of 1962 proved that it is possible to use multiplicative staging whereby lower yield primary nuclear explosions trigger off a fusion stage 1,000 times more powerful than its initiator. OK, the first laser fusion ignitions last year only multiplied the supplied input energy by a factor that's closer to 2 than to the impressive 1,000 of the 1962 Ripple II nuclear warhead, but the problems and solutions are known and the whole basis of NIF for practical fusion power is improve this technology. (The first computers were far more than 1,000 times as bulky and less efficient than those available after a few years of very hard-graft research and development.) Even if initial-stage multiplications are far lower than 1,000, you can simply add more small stages to get around this (they are tiny and won't take up a huge volume or mass in the warhead). The later stages will definitely have less asymmetry problems (as in Ripple II), and we know from the Ripple II test back in 1962 that you can definitely multiply by a factor of 1,000 to get from 10 kilotons to 10 megatons in a single multiplicative stage! Another key factor, as shown on our graph linked here, is that you can use cheap natural LiD as fuel once you have a successful D+T reaction, because naturally abundant, cheap Li-7 more readily fissions to yield tritium with the 14.1 MeV neutrons from D+T fusion, than expensively enriched Li-6, which is needed to make tritium in nuclear reactors where the fission neutron energy of around 1 MeV is too low to to fission Li-7.
It should also be noted that despite an openly published paper about Nuckolls' Ripple II success being stymied in 2021 by Jon Grams, the subject is still being covered up/ignored by the anti-nuclear biased Western media! Grams article fails to contain the design details such as the isentropic power delivery curve etc from Nuckolls' declassified articles that we include in the latest blog post here. One problem regarding "data" causing continuing confusion about the Dominic-Housatonic 30 October 1962 Ripple II test at Christmas Island, is made clear in the DASA-1211 report's declassified summary of the sizes, weights and yields of those tests: Housatonic was Nuckolls' fourth and final isentropic test, with the nuclear system inserted into a heavy steel Mk36 drop case, making the overall size 57.2 inches in diameter, 147.9 long and 7,139.55 lb mass, i.e. 1.4 kt/lb or 3.0 kt/kg yield-to-mass ratio for 9.96 Mt yield, which is not impressive for that yield range until you consider (a) that it was 99.9% fusion and (b) the isentropic design required a heavy holhraum around the large Ripple II fusion secondary stage to confine x-rays for relatively long time during which a slowly rising pulse of x-rays were delivered from the primary to secondary via a very large areas of foam elsewhere in the weapon, to produce isentropic compression. Additionally, the test was made in a hurry before an atmospheric teat ban treaty, and this rushed use of a standard air drop steel casing made the tested weapon much heavier than a properly weaponized Ripple II. The key point is that a 10 kt fission device set off a ~10 Mt fusion explosion, a very clean deterrent. Applying this Ripple II 1,000-factor multiplicative staging figure directly to this technology for clean nuclear warheads, a 0.5 kg TNT D+T fusion capsule would set off a 0.5 ton TNT 2nd stage of LiD, which would then set off a 0.5 kt 3rd stage "neutron bomb", which could then be used to set off a 500 kt 4th stage or "strategic nuclear weapon". It is therefore now possible not just in principle but in practice, using suitable already-proved technical staging systems used in 1960s nuclear weapon tests successfully, to design 100% clean fusion nuclear warheads! Yes, the details have been worked out, yes the technology has been tested in piecemeal fashion. All that is now needed is a new, but quicker and cheaper, Star Wars program or Manhattan Project style effort to pull the components together. This will constitute a major leap forward in the credibility of the deterrence of aggressors.
ABOVE: as predicted, the higher the x-ray input laser pulse for the D+T initiator of a clean multiplicatively-staged nuclear deterrent, the lower the effect of plasma instabilities and asymmetries and the greater the fusion burn. To get ignition (where the x-ray energy injected into the fusion hohlraum by the laser is less than the energy released in the D+T fusion burn) they have had to use about 2 MJ delivered in 10 ns or so, equivalent to 0.5 kg of TNT equivalent. But for deterrent use, why use such expensive, delicate x-ray lasers? Why not just use one-shot miniaturised x-ray tubes with megavolt electron acceleration, powered a suitably ramped pulse from a chemical explosion for magnetic flux compression current generation? At 10% efficiency, you need 0.5 x 10 = 5 kg of TNT! Even at 1% efficiency, 50 kg of TNT will do. Once the D+T gas capsule's hohlraum is well over 1 cm in size, to minimise the risk of imperfections that cause asymmetries, you don't any longer need focussed laser beams to enter tiny apertures. You might even be able to integrate many miniature flash x-ray tubes (each designed to burn out when firing one pulse of a MJ or so) into a special hohlraum. Humanity urgently needs a technological arms race akin to Reagan's Star Wars project, to deter the dictators from invasions and WWIII. In the conference video above, a question was asked about the real efficiency of the enormous repeat-pulse capable laser system's efficiency (not required for a nuclear weapon whose components only require the capability to be used once, unlike lab equipment): the answer is that 300 MJ was required by the lab lasers to fire a 2 MJ pulse into the D+T capsule's x-ray hohlraum, i.e. their lasers are only 0.7% efficient! So why bother? We know - from the practical use of incoherent fission primary stage x-rays to compress and ignite fusion capsules in nuclear weapons - that you simply don't need coherent x-rays from a laser for this purpose. The sole reason they are approaching the problem with lasers is that they began their lab experiments decades ago with microscopic sized fusion capsules and for those you need a tightly focussed beam to insert energy through a tiny hohlraum aperture. But now they are finally achieving success with much larger fusion capsules (to minimise instabilities that caused the early failures), it may be time to change direction. A whole array of false "no-go theorems" can and will be raised by ignorant charlatan "authorities" against any innovation; this is the nature of the political world. There is some interesting discussion of why clean bombs aren't in existence today, basically the idealized theory (which works fine for big H-bombs but ignores small-scale asymmetry problems which are important only at low ignition energy) understimated the input energy required for fusion ignition by a factor of 2000:
"The early calculations on ICF (inertial-confinement fusion) by John Nuckolls in 1972 had estimated that ICF might be achieved with a driver energy as low as 1 kJ. ... In order to provide reliable experimental data on the minimum energy required for ignition, a series of secret experiments—known as Halite at Livermore and Centurion at Los Alamos—was carried out at the nuclear weapons test site in Nevada between 1978 and 1988. The experiments used small underground nuclear explosions to provide X-rays of sufficiently high intensity to implode ICF capsules, simulating the manner in which they would be compressed in a hohlraum. ... the Halite/Centurion results predicted values for the required laser energy in the range 20 to 100MJ—higher than the predictions ..." - Garry McCracken and Peter Stott, Fusion, Elsevier, 2nd ed., p149.
In the final diagram above, we illustrate an example of what could very well occur in the near future, just to really poke a stick into the wheels of "orthodoxy" in nuclear weapons design: is it possible to just use a lot of (perhaps hardened for higher currents, perhaps no) pulsed current driven microwave tubes from kitchen microwave ovens, channelling their energy using waveguides (simply metal tubes, i.e. electrical Faraday cages, which reflect and thus contain microwaves) into the hohlraum, and make the pusher of dipole molecules (like common salt, NaCl) which is a good absorber of microwaves (as everybody knows from cooking in microwave ovens)? It would be extremely dangerous, not to mention embarrassing, if this worked, but nobody had done any detailed research into the possibility due to groupthink orthodoxy and conventional boxed in thinking! Remember, the D+T capsule just needs extreme compression and this can be done by any means that works. Microwave technology is now very well-established. It's no good trying to keep anything of this sort "secret" (either officially or unofficially) since as history shows, dictatorships are the places where "crackpot"-sounding ideas (such as douple-primary Project "49" Russian thermonuclear weapon designs, Russian Sputnik satellites, Russian Novichok nerve agent, Nazi V1 cruise missiles, Nazi V2 IRBM's, etc.) can be given priority by loony dictators. We have to avoid, as Edward Teller put it (in his secret commentary debunking Bethe's false history of the H-bomb, written AFTER the Teller-Ulam breakthrough), "too-narrow" thinking (which Teller said was still in force on H-bomb design even then). Fashionable hardened orthodoxy is the soft underbelly of "democracy" (a dictatorship by the majority, which is always too focussed on fashionable ideas and dismissive of alternative approaches in science and technology). Dictatorships (minorities against majorities) have repeatedly demonstrated a lack of concern for the fake "no-go theorems" used by Western anti-nuclear "authorities" to ban anything but fashionable groupthink science.
In the diagram below, it appears that the Mk17 only had a single secondary stage like the similar yield 1952 Mike design. The point here is that popular misunderstanding of the simple mechanism of x-ray energy transfer for higher yield weapons may be creating a dogmatic attitude even in secret nuclear weaponeer design labs, where orthodoxy is followed too rigorously. The Russians (see quotes on the latest blog post here) state they used two entire two-stage thermonuclear weapons with a combined yield of 1 megaton to set off their 50 megaton test in 1961. If true, you can indeed use two-stage hydrogen bombs as an "effective primary" to set off another secondary stage, of much higher yield. Can this be reversed in the sense of scaling it down so you have several bombs-within-bombs, all triggered by a really tiny first stage? In other words, can it be applied to neutron bomb design?
Update (15 Dec 2023): PDF uploaded of UK DAMAGE BY NUCLEAR WEAPONS (linked here on Internet Archive) - secret 1000 pages UK and USA nuclear weapon test effects analysis, and protective measures determined at those tests (not guesswork) relevant to escalation threats by Russia for EU invasion (linked here at wordpress) in response to Ukraine potentially joining the EU (this is now fully declassified without deletions, and in the UK National Archives at Kew):ABOVE: some pages from the originally SECRET ATOMIC 1,000 pages long UK Government Damage by Nuclear Weapons manual (now totally declassified without any deletions of data - unlike American manuals - in the UK National Archives, Kew), summarizing all of the effects data from 1950s British and American atmospheric nuclear weapons tests on military targets and also civil defense shelters tests, costs and safety. Below: some extracts from reports on Australian-British nuclear weapon test operations at Maralinga in 1956 and 1957, Buffalo and Antler, proved that even at 10 psi peak overpressure for the 15 kt Buffalo-1 shot, the dummy lying prone facing the blast was hardly moved due to the low cross-sectional area exposed to the blast winds, relative to standing dummies which were severely displaced and damaged. The value of trenches in protecting personnel against blast winds and radiation was also proved in tests (gamma radiation shielding of trenches had been proved at an earlier nuclear test in Australian, Operation Hurricane in 1952). (Antler report linked here; Buffalo report linked here.) All of this is still omitted from the American Glasstone and Dolan book "The Effects of Nuclear Weapons". The 1996 Northrop EM-1 (see extracts below showing protection by modern buildings and also simple shelters very close to nuclear tests; note that Northrop's entire set of damage ranges as a function of yield for underground shelters, tunnels, silos are based on two contained deep underground nuclear tests of different yield scaled to surface burst using the assumption of 5% yield ground coupling relative to the underground shots; this 5% equivalence figure appears to be an exaggeration for compact modern warheads, e.g. the paper “Comparison of Surface and Sub-Surface Nuclear Bursts,” from Steven Hatch, Sandia National Laboratories, to Jonathan Medalia, October 30, 2000, shows a 2% equivalence, e.g. Hatch shows that 1 megaton surface burst produces identical ranges to underground targets as a 20 kt burst at >20m depth of burst, whereas Northrop would require 50kt) has not been openly published, despite such protection being used in Russia! This proves heavy bias against credible tactical nuclear deterrence of the invasions that trigger major wars that could escalate into nuclear war (Russia has 2000+ dedicated neutron bombs; we don't!) and against simple nuclear proof tested civil defence which makes such deterrence credible and of course is also of validity against conventional wars, severe weather, peacetime disasters, etc. The basic fact is that nuclear weapons can deter/stop invasions unlike the conventional weapons that cause mass destruction, and nuclear collateral damage is eliminated easily for nuclear weapons by using them on military targets, since at collateral damage distances all the effects are sufficiently delayed in arrival (unlike the case for the smaller areas affected by conventional weapons). As for Hitler's stockpile of 12,000 tons of tabun nerve gas, whose use was deterred by proper defences (gas masks for all civilians, as well as biological agent anthrax and mustard gas retaliation capacity), it is possible to deter escalation within a world war with a crazy terrorist if people are protected by defence and deterrence:
J. R. Oppenheimer (opposing Teller), February 1951: "It is clear that they can be used only as adjuncts in a military campaign which has some other components, and whose purpose is a military victory. They are not primarily weapons of totality or terror, but weapons used to give combat forces help they would otherwise lack. They are an integral part of military operations. Only when the atomic bomb is recognized as useful insofar as it is an integral part of military operations, will it really be of much help in the fighting of a war, rather than in warning all mankind to avert it." (Quotation: Samuel Cohen, Shame, 2nd ed., 2005, page 99.)
‘The Hungarian revolution of October and November 1956 demonstrated the difficulty faced even by a vastly superior army in attempting to dominate hostile territory. The [Soviet Union] Red Army finally had to concentrate twenty-two divisions in order to crush a practically unarmed population. ... With proper tactics, nuclear war need not be as destructive as it appears when we think of [World War II nuclear city bombing like Hiroshima]. The high casualty estimates for nuclear war are based on the assumption that the most suitable targets are those of conventional warfare: cities to interdict communications ... With cities no longer serving as key elements in the communications system of the military forces, the risks of initiating city bombing may outweigh the gains which can be achieved. ...
‘The elimination of area targets will place an upper limit on the size of weapons it will be profitable to use. Since fall-out becomes a serious problem [i.e. fallout contaminated areas which are so large that thousands of people would need to evacuate or shelter indoors for up to two weeks] only in the range of explosive power of 500 kilotons and above, it could be proposed that no weapon larger than 500 kilotons will be employed unless the enemy uses it first. Concurrently, the United States could take advantage of a new development which significantly reduces fall-out by eliminating the last stage of the fission-fusion-fission process.’
- Dr Henry Kissinger, Nuclear Weapons and Foreign Policy, Harper, New York, 1957, pp. 180-3, 228-9.
(Quoted in 2006 on this blog here.)ABOVE: 16 February 1950 Daily Express editorial on H Bomb problem due to the fact that the UN is another virtue signalling but really war mongering League of Nations (which oversaw Nazi appeasement and the outbreak of WWII); however Fuchs had attended the April 1946 Super Conference during which the Russian version of the H-bomb involving isentropic radiation implosion of a separate low-density fusion stage (unlike Teller's later dense metal ablation rocket implosion secondary TX14 Alarm Clock and Sausage designs) were discussed and then given to Russia. The media was made aware only that Fuchs hade given the fission bomb to Russia. The FBI later visited Fuchs in British jail, showed him a film of Harry Gold (whom Fuchs identified as his contact while at Los Alamos) and also gave Fuchs a long list of secret reports to mark off individually so that they knew precisely what Stalin had been given. Truman didn't order H-bomb research and development because Fuchs gave Stalin the A-bomb, but because he gave them the H-bomb. The details of the Russian H-bomb are still being covered up by those who want a repetition of 1930s appeasement, or indeed the deliberate ambiguity of the UK Cabinet in 1914 which made it unclear what the UK would do if Germany invaded Belgium, allowing the enemy to exploit that ambiguity, starting a world war. The key fact usually covered up (Richard Rhodes, Chuck Hansen, and the whole American "expert nuclear arms community" all misleadingly claim that Teller's Sausage H-bomb design with a single primary and a dense ablator around a cylindrical secondary stage - uranium, lead or tungsten - is the "hydrogen bomb design") here is that two attendees of the April 1946 Super Conference, the report author Egon Bretscher and the radiation implosion discoverer Klaus Fuchs - were British, and both contributed key H-bomb design principles to the Russian and British weapons (discarded for years by America). Egon Bretscher for example wrote up the Super Conference report, during which attendees suggested various ways to try to achieve isentropic compression of low-density fusion fuel (a concept discarded by Teller's 1951 Sausage design, but used by Russia and re-developed in America on Nuckolls 1962 Ripple tests), and after Teller left Los Alamos, Bretscher took over work on Teller's Alarm Clock layered fission-fusion spherical hybrid device before Bretscher himself left Los Alamos and became head of nuclear physics at Harwell, UK,, submitting UK report together with Fuchs (head of theoretical physics at Harwell) which led to Sir James Chadwick's UK paper on a three-stage thermonuclear Super bomb which formed the basis of Penney's work at the UK Atomic Weapons Research Establishment. While Bretscher had worked on Teller's hybrid Alarm Clock (which originated two months after Fuchs left Los Alamos), Fuchs co-authored a hydrogen bomb patent with John von Neumann, in which radiation implosion and ionization implosion was used. Between them, Bretscher and Fuchs had all the key ingredients. Fuchs leaked them to Russia and the problem persists today in international relations.
There are four ways of dealing with aggressors: conquest (fight them), intimidation (deter them), fortification (shelter against their attacks; historically used as castles, walled cities and even walled countries in the case of China's 1,100 mile long Great Wall and Hadrian's Wall, while the USA has used the Pacific and Atlantic as successful moats against invasion, at least since Britain invaded Washington D.C. back in 1812), and friendship (which if you are too weak to fight, means appeasing them, as Chamberlain shook hands with Hitler for worthless peace promises). These are not mutually exclusive: you can use combinations. If you are very strong in offensive capability and also have walls to protect you while your back is turned, you can - as Teddy Roosevelt put it (quoting a West African proverb): "Speak softly and carry a big stick." But if you are weak, speaking softly makes you a target, vulnerable to coercion. This is why we don't send troops directly to Ukraine. When elected in 1960, Kennedy introduced "flexible response" to replace Dulles' "massive retaliation", by addressing the need to deter large provocations without being forced to decide between the unwelcome options of "surrender or all-out nuclear war" (Herman Kahn called this flexible response "Type 2 Deterrence"). This was eroded by both Russian civil defense and their emerging superiority in the 1970s: a real missiles and bombers gap emerged in 1972 when the USSR reached and then exceeded the 2,200 of the USA, while in 1974 the USSR achieve parity at 3,500 equivalent megatons (then exceeded the USA), and finally today Russia has over 2,000 dedicated clean enhanced neutron tactical nuclear weapons and we have none (except low-neutron output B61 multipurpose bombs). (Robert Jastrow's 1985 book How to make nuclear Weapons obsolete was the first to have graphs showing the downward trend in nuclear weapon yields created by the development of miniaturized MIRV warheads for missiles and tactical weapons: he shows that the average size of US warheads fell from 3 megatons in 1960 to 200 kilotons in 1980, and from a total of 12,000 megatons in 1960 to 3,000 megatons in 1980.)
The term "equivalent megatons" roughly takes account of the fact that the areas of cratering, blast and radiation damage scale not linearly with energy but as something like the 2/3 power of energy release; but note that close-in cratering scales as a significantly smaller power of energy than 2/3, while blast wind drag displacement of jeeps in open desert scales as a larger power of energy than 2/3. Comparisons of equivalent megatonnage shows, for example, that WWII's 2 megatons of TNT in the form of about 20,000,000 separate conventional 100 kg (0.1 ton) explosives is equivalent to 20,000,000 x (10-7)2/3 = 431 separate 1 megaton explosions! The point is, nuclear weapons are not of a different order of magnitude to conventional warfare, because: (1) devastated areas don't scale in proportion to energy release, (2) the number of nuclear weapons is very much smaller than the number of conventional bombs dropped in conventional war, and (3) because of radiation effects like neutrons and intense EMP, it is possible to eliminate physical destruction by nuclear weapons by a combination of weapon design (e.g. very clean bombs like 99.9% fusion Dominic-Housatonic, or 95% fusion Redwing-Navajo) and burst altitude or depth for hard targets, and create a weapon that deters invasions credibly (without lying local fallout radiation hazards), something none of the biased "pacifist disarmament" lobbies (which attract Russian support) tell you! There's a big problem with propaganda here.
ILLUSTRATION: the threat of WWII and the need to deter it was massively derided by popular pacifism which tended to make "jokes" of the Nazi threat until too late (example of 1938 UK fiction on this above; Charlie Chaplin's film "The Great Dictator" is another example), so three years after the Nuremberg Laws and five years after illegal rearmament was begun by the Nazis, in the UK crowds of "pacifists" in Downing Street, London, support friendship with the top racist, dictatorial Nazis in the name of "world peace". The Prime Minister used underhand techniques to try to undermine appeasement critics like Churchill and also later to get W. E. Johns fired from both editorships of Flying (weekly) and Popular Flying (monthly) to make it appear everybody "in the know" agreed with his actions, hence the contrived "popular support" for collaborating with terrorists depicted in these photos. The same thing persists today; in the 1920s and 1930s "pacifist" was driven by claims explosions, fire and poison gas will kill everybody in a knockout blow immediately war breaks out.
Update (30 January 2024): on the important world crisis, https://vixra.org/abs/2312.0155 gives a detailed review of "Britain and the H-bomb" (linked here), and why the "nuclear deterrence issue" isn't about "whether we should deter evil", but precisely what design of nuclear warhead we should have in order to do that cheaply, credibly, safely, and efficiently without guaranteeing either escalation or the failure of deterrence. When we disarmed our chemical and biological weapons, it was claimed that the West could easily deter those weapons using strategic nuclear weapons to bomb Moscow (which has shelters, unlike us). That failed when Putin used sarin and chlorine to prop up Assad in Syria, and Novichok in the UK to kill Dawn Sturgess in 2018. So it's just not a credible deterrent to say you will bomb Moscow if Putin invades Europe or uses his 2000 tactical nuclear weapons. An even more advanced deterrent, the 100% clean very low yield (or any yield) multiplicative staged design without any fissile material whatsoever, just around the corner. Clean secondary stages have been proof-tested successfully for example in the 100% clean Los Alamos Redwing Navajo secondary, and the 100% clean Ripple II secondary tested 30 October 1962, and the laser ignition of very tiny fusion capsules to yield more energy than supplied has been done on 5 December 2022 when a NIF test delivered 2.05 MJ (the energy of about 0.5 kg of TNT) to a fusion capsule which yielded 3.15 MJ, so all that is needed is to combine both ideas in a system whereby suitably sized second stages - ignited in the first place by a capacitative charged circuit sending a pulse of energy to a suitable laser system (the schematic shown is just a sketch of principle - more than one laser would possibly be required for reliability of fusion ignition) acting on tiny fusion capsule as shown - are encased to two-stage "effective primaries" which each become effective primaries of bigger systems, thus a geometric series of multiplicative staging until the desired yield is reached. Note that the actual tiny first T+D capsule can be compressed by one-shot lasers - compact lasers used way beyond their traditional upper power limit and burned out in a firine a single pulse - in the same way the gun assembly of the Hiroshima bomb was based on a one-shot gun. In other words, forget all about textbook gun design. The Hiroshima bomb gun assembly system only had to be fired once unlike a field artillery piece which has to be fired many thousands of times before metal fatigue sets in. Thus, by analogy, the lasers - which can be powered by ramping current pulses from magnetic flux compressor systems - for use in a clean bomb will be much smaller and lighter than current lab gear which is designed to be used thousands of times in repeated experiments. The diagram below shows cylindrical Li6D stages throughout for a compact bomb shape, but spherical stages can be used, and once a few stages get fired, the flux of 14 MeV neutrons is sufficient to go to cheap natural LiD. To fit it into a MIRV warhead, the low density of LiD constrains such a clean warhead will have a low nuclear yield, which means a tactical Cohen type neutron deterrent of the invasions that cause big wars. It should also be noted that in 1944 von Neumann suggested that T + D inside the core of the fission weapon would be compressed by "ionization compression" during fission (where a higher density ionized plasma compresses a lower density ionized plasma, i.e. the D + T plasma), an idea that was - years later - named the Internal Booster principle by Teller; see Frank Close, "Trinity", Allen Lane, London, 2019, pp158-159 where Close argues that during the April 1946 Superbomb Conference, Fuchs extended von Neumann's 1944 internal fusion boosting idea to an external D + T filled BeO walled capsule:
"Fuchs reasoned that [the very low energy, 1-10 kev, approximately 10-100 lower energy than medical] x-rays from the [physically separated] uranium explosion would reach the tamper of beryllium oxide, heat it, ionize the constituents and cause them to implode - the 'ionization implosion' concept of von Neumann but now applied to deuterium and tritium contained within beryllium oxide. To keep the radiation inside the tamper, Fuchs proposed to enclose the device inside a casing impervious to radiation. The implosion induced by the radiation would amplify the compression ... and increase the chance of the fusion bomb igniting. The key here is 'separation of the atomic charge and thermonuclear fuel, and compression of the latter by radiation travelling from the former', which constitutes 'radiation implosion'."
(This distinction between von Neumann's "ionization implosion" INSIDE the tamper, of denser tamper expanding and thus compressing lower density fusion fuel inside, and Fuchs' OUTSIDE capsule "radiation implosion", is key even today for isentropic H-bomb design; it seems Teller's key breakthroughs were not separate stages or implosion but rather radiation mirrors and ablative recoil shock compression, where radiation is used to ablate a dense pusher of Sausage designs like Mike in 1952 etc., a distinction not to be confused for the 1944 von Neumann and 1946 Fuchs implosion mechanisms! It appears Russian H-bombs used von Neumann's "ionization implosion" and Fuchs's "radiation implosion" for RDS-37 on 22 November 1955 and also in their double-primary 23 February 1958 test and subsequently, where their fusion capsules reportedly contained a BeO or other low-density outer coating, which would lead to quasi-isentropic compression, more effective for low density secondary stages than purely ablative recoil shock compression. This accounts for the continuing classification of the April 1946 Superbomb Conference (the extract of 32 pages linked here is so severely redacted that it is less helpful than the brief but very lucid summary of its technical content, in the declassified FBI compilation of reports concerning data Klaus Fuchs sent to Stalin, linked here!). Teller had all the knowledge he needed in 1946, but didn't go ahead because he made the stupid error of killing progress off by his own "no-go theorem" against compression of fusion fuel. Teller did a "theoretical" calculation in which he claimed that compression has no effect on the amount of fusion burn because the compressed system is simply scaled down in size so that the same efficiency of fusion burn occurs, albeit faster, and then stops as the fuel thermally expands. This was wrong. Teller discusses the reason for his great error in technical detail during his tape-recorded interview by Chuck Hansen at Los Alamos on 7 June 1993 (C. Hansen, Swords of Armageddon, 2nd ed., pp. II-176-7):
"Now every one of these [fusion] processes varied with the square of density. If you compress the thing, then in one unit's volume, each of the 3 important processes increased by the same factor ... Therefore, compression (seemed to be) useless. Now when ... it seemed clear that we were in trouble, then I wanted very badly to find a way out. And it occurred to be than an unprecedentedly strong compression will just not allow much energy to go into radiation. Therefore, something had to be wrong with my argument and then, you know, within minutes, I knew what must be wrong ... [energy] emission occurs when an electron and a nucleus collide. Absorption does not occur when a light quantum and a nucleus ... or ... electron collide; it occurs when a light quantum finds an electron and a nucleus together ... it does not go with the square of the density, it goes with the cube of the density." (This very costly theoretical error, wasting five years 1946-51, could have been resolved by experimental nuclear testing. There is always a risk of this in theoretical physics, which is why experiments are done to check calculations before prizes are handed out. The ban on nuclear testing is a luddite opposition to technological progress in improving deterrence.)
(This 1946-51 theoretical "no-go theorem" anti-compression error of Teller's, which was contrary to the suggestion of compression at the April 1946 superbomb conference as Teller himself refers to on 14 August 1952, and which was corrected only by comparison of the facts about compression validity in pure fission cores in Feb '51 after Ulam's argument that month for fission core compression by lens focussed primary stage shock waves, did not merely lead to Teller's dismissal of vital compression ideas. It also led to his false equations - exaggerating the cooling effect of radiation emission - causing underestimates of fusion efficiency in all theoretical calculations done of fusion until 1951! For this reason, Teller later repudiated the calculations that allegedly showed his Superbomb would fizzle; he argued that if it had been tested in 1946, the detailed data obtained - regardless of whatever happened - would have at least tested the theory which would have led to rapid progress, because the theory was wrong. The entire basis of the cooling of fusion fuel by radiation leaking out was massively exaggerated until Lawrence Livermore weaponeer John Nuckolls showed that there is a very simple solution: use baffle re-radiated, softened x-rays for isentropic compression of low-density fusion fuel, e.g. very cold 0.3 kev x-rays rather than the usual 1-10 kev cold-warm x-rays emitted directly from the fission primary. Since the radiation losses are proportional to the fourth-power of the x-ray energy or temperature, losses are virtually eliminated, allowing very efficient staging as for Nuckolls' 99.9% 10 Mt clean Ripple II, detonated on 30 October 1962 at Christmas Island. Teller's classical Superbomb was actually analyzed by John C. Solem in a 15 December 1978 report, A modern analysis of Classical Super, LA-07615, according to a Freedom of Information Act request filed by mainstream historian Alex Wellerstein, FOIA 17-00131-H, 12 June 2017; according to a list of FOIA requests at https://www.governmentattic.org/46docs/NNSAfoiaLogs_2016-2020.pdf. However, a google search for the documents Dr Wellerstein requested shows only a few at the US Gov DOE Opennet OSTI database or otherwise online yet e.g. LA-643 by Teller, On the development of Thermonuclear Bombs dated 16 Feb. 1950. The page linked here stating that report was "never classified" is mistaken! One oddity about Teller's anti-compression "no-go theorem" is that the even if fusion rates were independent of density, you would still want compression of fissile material in a secondary stage such as a radiation imploded Alarm Clock, because the whole basis of implosion fission bombs is the benefit of compression; another issue is that even if fusion rates are unaffected by density, inward compression would still help to delay the expansion of the fusion system which leads to cooling and quenching of the fusion burn.)
ABOVE: the FBI file on Klaus Fuchs contains a brief summary of the secret April 1946 Super Conference at Los Alamos which Fuchs attended, noting that compression of fusion fuel was discussed by Lansdorf during the morning session on 19 April, attended by Fuchs, and that: "Suggestions were made by various people in attendance as to the manner of minimizing the rise in entropy during compression." This fact is vitally interesting, since it proves that an effort was being made then to secure isentropic compression of low-density fusion fuel in April 1946, sixteen years before John H. Nuckolls tested the isentropically compressed Ripple II device on 30 October 1962, giving a 99.9% clean 10 megaton real H-bomb! So the Russians were given a massive head start on this isentropic compression of low-density fusion fuel for hydrogen bombs, used (according to Trutnev) in both the single primary tests like RDS-37 in November 1955 and also in the double-primary designs which were 2.5 times more efficient on a yield-to-mass basis, tested first on 23 February 1958! According to the FBI report, the key documents Fuchs gave to Russia were LA-551, Prima facie proof of the feasibility of the Super, 15 Apr 1946 and the LA-575 Report of conference on the Super, 12 June 1946. Fuchs also handed over to Russia his own secret Los Alamos reports, such as LA-325, Initiator Theory, III. Jet Formation by the Collision of Two Surfaces, 11 July 1945, Jet Formation in Cylindrical lmplosion with 16 Detonation Points, Secret, 6 February 1945, and Theory of Initiators II, Melon Seed, Secret, 6 January 1945. Note the reference to Bretscher attending the Super Conference with Fuchs; Teller in a classified 50th anniversary conference at Los Alamos on the H-bomb claimed that after he (Teller) left Los Alamos for Chicago Uni in 1946, Bretscher continued work on Teller's 31 August 1946 "Alarm Clock" nuclear weapon (precursor of the Mike sausage concept etc) at Los Alamos; it was this layered uranium and fusion fuel "Alarm Clock" concept which led to the departure of Russian H-bomb design from American H-bomb design, simply because Fuchs left Los Alamos in June 1946, well before Teller invented the Alarm Clock concept on 31 August 1946 (Teller remembered the date precisely simply because he invented the Alarm Clock on the day his daughter was born, 31 August 1946! Teller and Richtmyer also developed a variant called "Swiss Cheese", with small pockets or bubbles of expensive fusion fuels, dispersed throughout cheaper fuel, in order to kinder a more cost-effective thermonuclear reaction; this later inspired the fission and fusion boosted "spark plug" ideas in later Sausage designs; e.g. security cleared Los Alamos historian Anne Fitzpatrick stated during her 4 March 1997 interview with Robert Richtmyer, who co-invented the Alarm Clock with Teller, that the Alarm Clock evolved into the spherical secondary stage of the 6.9 megaton Castle-Union TX-14 nuclear weapon!).
In fact (see Lawrence Livermore National Laboratory nuclear warhead designer Nuckolls' explanation in report UCRL-74345): "The rates of burn, energy deposition by charged reaction products, and electron-ion heating are proportional to the density, and the inertial confinement time is proportional to the radius. ... The burn efficiency is proportional to the product of the burn rate and the inertial confinement time ...", i.e. the fusion burn rate is directly proportional to the fuel density, which in turn is of course inversely proportional to the cube of its radius. But the inertial confinement time for fusion to occur is proportional to the radius, so the fusion stage efficiency in a nuclear weapon is the product of the burn rate (i.e., 1/radius^3) and time (i.e., radius), so efficiency ~ radius/(radius^3) ~ 1/radius^2. Therefore, for a given fuel temperature, the total fusion burn, or the efficiency of the fusion stage, is inversely proportional to the square of the compressed radius of the fuel! (Those condemning Teller's theoretical errors or "arrogance" should be aware that he pushed hard all the time for experimental nuclear tests of his ideas, to check if they were correct, exactly the right thing to do scientifically and others who read his papers had the opportunity to point out any theoretical errors, but was rebuffed by those in power, who used a series of contrived arguments to deny progress, based upon what Harry would call "subconscious bias", if not arrogant, damning, overt bigotry against the kind of credible, overwhelming deterrence which had proved lacking a decade earlier, leading to WWII. This callousness towards human suffering in war and under dictatorship existed in some UK physicists too: Joseph Rotblat's hatred of anything to deter Russia be it civil defense or tactical neutron bombs of the West - he had no problem smiling and patting Russia's neutron bomb when visiting their labs during cosy groupthink deluded Pugwash campaigns for Russian-style "peaceful collaboration" - came from deep family communist convictions, since his brother was serving in the Red Army in 1944 when he alleged he heard General Groves declare that the bomb must deter Russia! Rotblat stated he left Los Alamos as a result. The actions of these groups are analogous to the "Cambridge Scientists Anti-War Group" in the 1930s. After Truman ordered a H-bomb, Bradbury at Los Alamos had to start a "Family Committee" because Teller had a whole "family" of H-bomb designs, ranging from the biggest, "Daddy", through various "Alarm Clocks", all the way down to small internally-boosted fission tactical weapons. From Teller's perspective, he wasn't putting all eggs in one basket.)
Above: declassified illustration from a January 1949 secret report by the popular physics author and Los Alamos nuclear weapons design consultant George Gamow, showing his suggestion of using x-rays from both sides of a cylindrically imploded fission device to expose two fusion capsules to x-rays to test whether compression (fusion in BeO box on right side) helps, or is unnecessary (capsule on left side). Neutron counters detect 14.1 Mev T+D neutrons using time-of-flight method (higher energy neutrons traver faster than ~1 Mev fission stage neutrons, arriving at detectors first, allowing discrimination of the neutron energy spectrum by time of arrival). It took over two years to actually fire this 225 kt shot (8 May 1951)! No wonder Teller was outraged. A few interesting reports by Teller and also Oppenheimer's secret 1949 report opposing the H bomb project as it then stood on the grounds of low damage per dollar - precisely the exact opposite of the "interpretation" the media and gormless fools will assert until the cows come home - are linked here. The most interesting is Teller's 14 August 1952 Top Secret paper debunking Hans Bethe's propaganda, by explaining that contrary to Bethe's claims, Stalin's spy Klaus Fuch had the key "radiation implosion"- see second para on p2 - secret of the H-bomb because he attended the April 1946 Superbomb Conference which was not even attended by Bethe! It was this very fact in April 1946, noted by two British attendees of the 1946 Superbomb Conference before collaboration was ended later in the year by the 1946 Atomic Energy Act, statement that led to Sir James Cladwick's secret use of "radiation implosion" for stages 2 and 3 of his triple staged H-bomb report the next month, "The Superbomb", a still secret document that inspired Penney's original Tom/Dick/Harry staged and radiation imploded H-bomb thinking, which is summarized by security cleared official historian Arnold's Britain and the H-Bomb. Teller's 24 March 1951 letter to Los Alamos director Bradbury was written just 15 days after his historic Teller-Ulam 9 March 1951 report on radiation coupling and "radiation mirrors" (i.e. plastic casing lining to re-radiate soft x-rays on to the thermonuclear stage to ablate and thus compress it), and states: "Among the tests which seem to be of importance at the present time are those concerned with boosted weapons. Another is connected vith the possibility of a heterocatalytic explosion, that is, implosion of a bomb using the energy from another, auxiliary bomb. A third concerns itself with tests on mixing during atomic explosions, which question is of particular importance in connection with the Alarm Clock."
There is more to Fuchs' influence on the UK H-bomb than I go into that paper; Chapman Pincher alleged that Fuchs was treated with special leniency at his trial and later he was given early release in 1959 because of his contributions and help with the UK H-bomb as author of the key Fuchs-von Neumann x-ray compression mechanism patent. For example, Penney visited Fuchs in June 1952 in Stafford Prison; see pp309-310 of Frank Close's 2019 book "Trinity". Close argues that Fuchs gave Penney a vital tutorial on the H-bomb mechanism during that prison visit. That wasn't the last help, either, since the UK Controller for Atomic Energy Sir Freddie Morgan wrote Penney on 9 February 1953 that Fuchs was continuing to help. Another gem: Close gives, on p396, the story of how the FBI became suspicious of Edward Teller, after finding a man of his name teaching at the NY Communist Workers School in 1941 - the wrong Edward Teller, of course - yet Teller's wife was indeed a member of the Communist-front "League of women shoppers" in Washington, DC.
Chapman Pincher, who attended the Fuchs trial, writes about Fuchs hydrogen bomb lectures to prisoners in chapter 19 of his 2014 autobiography, Dangerous to know (Biteback, London, pp217-8): "... Donald Hume ... in prison had become a close friend of Fuchs ... Hume had repaid Fuchs' friendship by organising the smuggling in of new scientific books ... Hume had a mass of notes ... I secured Fuchs's copious notes for a course of 17 lectures ... including how the H-bomb works, which he had given to his fellow prisoners ... My editor agreed to buy Hume's story so long as we could keep the papers as proof of its authenticity ... Fuchs was soon due for release ..."
Chapman Pincher wrote about this as the front page exclusive of the 11 June 1952 Daily Express, "Fuchs: New Sensation", the very month Penney visited Fuchs in prison to receive his H-bomb tutorial! UK media insisted this was evidence that UK security still wasn't really serious about deterring further nuclear spies, and the revelations finally culminated in the allegations that the MI5 chief 1956-65 Roger Hollis was a Russian fellow-traveller (Hollis was descended from Peter the Great, according to his elder brother Chris Hollis' 1958 book Along the Road to Frome) and GRU agent of influence, codenamed "Elli". Pincher's 2014 book, written aged 100, explains that former MI5 agent Peter Wright suspected Hollis was Elli after evidence collected by MI6 agent Stephen de Mowbray was reported to the Cabinet Secretary. Hollis is alleged to have deliberately fiddled his report of interviewing GRU defector Igor Gouzenko on 21 November 1945 in Canada. Gouzenko had exposed the spy and Groucho Marx lookalike Dr Alan Nunn May (photo below), and also a GRU spy in MI5 codenamed Elli, who used only duboks (dead letter boxes), but Gouzenko told Pincher that when Hollis interviewed him in 1945 he wrote up a lengthy false report claiming to discredit many statements by Gouzenko: "I could not understand how Hollis had written so much when he had asked me so little. The report was full of nonsense and lies. As [MI5 agent Patrick] Stewart read the report to me [during the 1972 investigation of Hollis], it became clear that it had been faked to destroy my credibility so that my information about the spy in MI5 called Elli could be ignored. I suspect that Hollis was Elli." (Source: Pincher, 2014, p320.) Christopher Andrew claimed Hollis couldn't have been GRU spy Elli because KGB defector Oleg Gordievsky suggested it was the KGB spy Leo Long (sub-agent of KGB spy Anthony Blunt). However, Gouzenko was GRU, not KGB like Long and Gordievsky! Gordievsky's claim that "Elli" was on the cover of Long's KGB file was debunked by KGB officer Oleg Tsarev, who found that Long's codename was actually Ralph! Another declassified Russian document, from General V. Merkulov to Stalin dated 24 Nov 1945, confirmed Elli was a GRU agent inside british intelligence, whose existence was betrayed by Gouzenko. In Chapter 30 of Dangerous to Know, Pincher related how he was given a Russian suitcase sized microfilm enlarger by 1959 Hollis spying eyewitness Michael J. Butt, doorman for secret communist meetings in London. According to Butt, Hollis delivered documents to Brigitte Kuczynski, younger sister of Klaus Fuchs' original handler, the notorious Sonia aka Ursula. Hollis allegedly provided Minox films to Brigitte discretely when walking through Hyde Park at 8pm after work. Brigitte gave her Russian made Minox film enlarger to Butt to dispose of, but he kept it in his loft as evidence. (Pincher later donated it to King's College.) Other more circumstantial evidence is that Hollis recruited the spy Philby, Hollis secured spy Blunt immunity from prosecution, Hollis cleared Fuchs in 1943, and MI5 allegedly destroyed Hollis' 1945 interrogation report on Gouzenko, to prevent the airing of the scandal that it was fake after checking it with Gouzenko in 1972.
It should be noted that the very small number of Russian GRU illegal agents in the UK and the very small communist party membership had a relatively large influence on nuclear policy via infiltration of unions which had block votes in the Labour Party, as well the indirect CND and "peace movement" lobbies saturating the popular press with anti-civil defence propaganda to make the nuclear deterrent totally incredible for any provocation short of a direct all-out countervalue attack. Under such pressure, UK Prime Minister Harold Wilson's government abolished the UK Civil Defence Corps, making the UK nuclear deterrent totally incredible against major provocations, in March 1968. While there was some opposition to Wilson, it was focussed on his profligate nationalisation policies which were undermining the economy and thus destabilizing military expenditure for national security. Peter Wright’s 1987 book Spycatcher and various other sources, including Daily Mirror editor Hugh Cudlipp's book Walking on Water, documented that on 8 May 1968, the Bank of England's director Cecil King, who was also Chairman of Daily Mirror newspapers, Mirror editor Cudlipp and the UK Ministry of Defence's anti-nuclear Chief Scientific Adviser Sir Solly Zuckerman, met at Lord Mountbatten's house in Kinnerton Street, London, to discuss a coup e'tat to overthrow Wilson and make Mountbatten the UK President, a new position. King's position, according to Cudlipp - quite correctly as revealed by the UK economic crises of the 1970s when the UK was effectively bankrupt - was that Wilson was setting the UK on the road to financial ruin and thus military decay. Zuckerman and Mountbatten refused to take part in a revolution, however Wilson's government was attacked by the Daily Mirror in a front page editorial by Cecil King two days later, on 10 May 1968, headlined "Enough is enough ... Mr Wilson and his Government have lost all credibility, all authority." According to Wilson's secretary Lady Falkender, Wilson was only told of the coup discussions in March 1976.
CND and the UK communist party alternatively tried to claim, in a contradictory way, that they were (a) too small in numbers to have any influence on politics, and (b) they were leading the country towards utopia via unilateral nuclear disarmament saturation propaganda about nuclear weapons annihilation (totally ignoring essential data on different nuclear weapon designs, yields, heights of burst, the "use" of a weapon as a deterrent to PREVENT an invasion of concentrated force, etc.) via the infiltrated BBC and most other media. Critics pointed out that Nazi Party membership in Germany was only 5% when Hitler became dictator in 1933, while in Russia there were only 200,000 Bolsheviks in September 1917, out of 125 million, i.e. 0.16%. Therefore, the whole threat of such dictatorships is a minority seizing power beyond it justifiable numbers, and controlling a majority which has different views. Traditional democracy itself is a dictatorship of the majority (via the ballot box, a popularity contest); minority-dictatorship by contrast is a dictatorship by the fanatically motivated minority by force and fear (coercion) to control the majority. The coercion tactics used by foreign dictators to control the press in free countries are well documented, but never publicised widely. Hitler put pressure on Nazi-critics in the UK "free press" via UK Government appeasers Halifax, Chamberlain and particularly the loathsome UK ambassador to Nazi Germany, Sir Neville Henderson, for example trying to censor or ridicule appeasement critics David Low, to fire Captain W. E. Johns (editor of both Flying and Popular Flying, which had huge circulations and attacked appeasement as a threat to national security in order to reduce rearmament expenditure), and to try to get Winston Churchill deselected. These were all sneaky "back door" pressure-on-publishers tactics, dressed up as efforts to "ease international tensions"! The same occurred during the Cold War, with personal attacks in Scientific American and Bulletin of the Atomic Scientists and by fellow travellers on Herman Kahn, Eugene Wigner, and others who warned we need civil defence to make a deterrent of large provocations credible in the eyes of an aggressor.
Chapman Pincher summarises the vast hypocritical Russian expenditure on anti-Western propaganda against the neutron bomb in Chapter 15, "The Neutron Bomb Offensive" of his 1985 book The Secret Offensive: "Such a device ... carries three major advantages over Hiroshima-type weapons, particularly for civilians caught up in a battle ... against the massed tanks which the Soviet Union would undoubtedly use ... by exploding these warheads some 100 feet or so above the massed tanks, the blast and fire ... would be greatly reduced ... the neutron weapon produces little radioactive fall-out so the long-term danger to civilians would be very much lower ... the weapon was of no value for attacking cities and the avoidance of damage to property can hardly be rated as of interest only to 'capitalists' ... As so often happens, the constant repetition of the lie had its effects on the gullible ... In August 1977, the [Russian] World Peace Council ... declared an international 'Week of action' against the neutron bomb. ... Under this propaganda Carter delayed his decision, in September ... a Sunday service being attended by Carter and his family on 16 October 1977 was disrupted by American demonstrators shouting slogans against the neutron bomb [see the 17 October 1977 Washington Post] ... Lawrence Eagleburger, when US Under Secretary of State for Political Affairs, remarked, 'We consider it probably that the Soviet campaign against the 'neutron bomb cost some $100 million'. ... Even the Politburo must have been surprised at the size of what it could regard as a Fifth Column in almost every country." [Unfortunately, Pincher himself had contributed to the anti-nuclear nonsense in his 1965 novel "Not with a bang" in which small amounts of radioactivity from nuclear fallout combine with medicine to exterminate humanity! The allure of anti-nuclear propaganda extends to all who which to sell "doomsday fiction", not just Russian dictators but mainstream media story tellers in the West. By contrast, Glasstone and Dolan's 1977 Effects of Nuclear Weapons doesn't even mention the neutron bomb, so there was no scientific and technical effort whatsoever by the West to make it a credible deterrent even in the minds of the public it had to protect from WWIII!]
This debunks fake news that Teller's and Ulam's 9 March 1951 report LAMS-1225 itself gave Los Alamos the Mike H-bomb design, ready for testing! Teller was proposing a series of nuclear tests of the basic principles, not 10Mt Ivy-Mike which was based on a report the next month by Teller alone, LA-1230, "The Sausage: a New Thermonuclear System". When you figure that, what did Ulam actually contribute to the hydrogen bomb? Nothing about implosion, compression or separate stages - all already done by von Neumann and Fuchs five years earlier - and just a lot of drivel about trying to channel material shock waves from a primary to compress another fissile core, a real dead end. What Ulam did was to kick Teller out of his self-imposed mental objection to compression devices. Everything else was Teller's; the radiation mirrors, the Sausage with its outer ablation pusher and its inner spark plug. Note also that contrary to official historian Arnold's book (which claims due to a misleading statement by Dr Corner that all the original 1946 UK copies of Superbomb Conference documentation were destroyed after being sent from AWRE Aldermaston to London between 1955-63), all the documents did exist in the AWRE TPN (theoretical physics notes, 100% of which have been perserved) and are at the UK National Archives, e.g. AWRE-TPN 5/54 is listed in National Archives discovery catalogue ref ES 10/5: "Miscellaneous super bomb notes by Klaus Fuchs", see also the 1954 report AWRE-TPN 6/54, "Implosion super bomb: substitution of U235 for plutonium" ES 10/6, the 1954 report AWRE-TPN 39/54 is "Development of the American thermonuclear bomb: implosion super bomb" ES 10/39, see also ES 10/21 "Collected notes on Fermi's super bomb lectures", ES 10/51 "Revised reconstruction of the development of the American thermonuclear bombs", ES 1/548 and ES 1/461 "Superbomb Papers", etc. Many reports are secret and retained, despite containing "obsolete" designs (although UK report titles are generally unredacted, such as: "Storage of 6kg Delta (Phase) -Plutonium Red Beard (tactical bomb) cores in ships")! It should also be noted that the Livermore Laboatory's 1958 TUBA spherical secondary with an oralloy (enriched U235) outer pusher was just a reversion from Teller's 1951 core spark plug idea in the middle of the fusion fuel, back to the 1944 von Neumann scheme of having fission material surrounding the fusion fuel. In other words, the TUBA was just a radiation and ionization imploded, internally fusion-boosted, second fission stage which could have been accomplished a decade earlier if the will existed, when all of the relevant ideas were already known. The declassified UK spherical secondary-stage alternatives linked here (tested as Grapple X, Y and Z with varying yields but similar size, since all used the 5 ft diameter Blue Danube drop casing) clearly show that a far more efficient fusion burn occurs by minimising the mass of hard-to-compress U235 (oralloy) sparkplug/pusher, but maximising the amount of lithium-7, not lithium-6. Such a secondary with minimal fissionable material also automatically has minimal neutron ABM vulnerability (i.e., "Radiation Immunity", RI). This is the current cheap Russian neutron weapon design, but not the current Western design of warheads like the W78, W88 and bomb B61.
So why on earth doesn't the West take the cheap efficient option of cutting expensive oralloy and maximising cheap natural (mostly lithium-7) LiD in the secondary? Even Glasstone's 1957 Effects of Nuclear Weapons on p17 (para 1.55) states that "Weight for weight ... fusion of deuterium nuclei would produce nearly 3 times as much energy as the fission of uranium or plutonium"! The sad answer is "density"! Natural LiD (containing 7.42% Li6 abundance) is a low density white/grey crystalline solid like salt that actually floats on water (lithium deuteroxide would be formed on exposure to water), since its density is just 820 kg/m^3. Since the ratio of mass of Li6D to Li7D is 8/9, it would be expected that the density of highly enriched 95% Li6D is 739 kg/m^3, while for 36% enriched Li6D it is 793 kg/m^3. Uranium metal has a density of 19,000 kg/m^3, i.e. 25.7 times greater than 95% enriched li6D or 24 times greater than 36% enriched Li6D. Compactness, i.e. volume is more important in a Western MIRV warhead than mass/weight! In the West, it's best to have a tiny-volume, very heavy, very expensive warhead. In Russia, cheapness outweights volume considerations. The Russians in some cases simply allowed their more bulky warheads to protrude from the missile bus (see photo below), or compensated for lower yields at the same volume using clean LiD by using the savings in costs to build more warheads. (The West doubles the fission yield/mass ratio of some warheads by using U235/oralloy pushers in place of U238, which suffers from the problem that about half the neutrons it interacts with result in non-fission capture, as explained below. Note that the 720 kiloton UK nuclear test Orange Herald device contained a hollow shell of 117 kg of U235 surrounded by a what Lorna Arnold's book quotes John Corner referring to a "very thin" layer of high explosive, and was compact, unboosted - the boosted failed to work - and gave 6.2 kt/kg of U235, whereas the first version of the 2-stage W47 Polaris warhead contained 60 kg of U235 which produced most of the secondary stage yield of about 400 kt, i.e. 6.7 kt/kg of U235. Little difference - but because perhaps 50% of the total yield of the W47 was fusion, its efficiency of use of U235 must have actually been less than the Orange Herald device, around 3 kt/kg of U235 which indicates design efficiency limits to "hydrogen bombs"! Yet anti-nuclear charlatans claimed that the Orange Herald bomb was a con!)
ABOVE: USA nuclear weapons data declassified by UK Government in 2010 (the information was originally acquired due to the 1958 UK-USA Act for Cooperation on the Uses of Atomic Energy for Mutual Defense Purposes, in exchange for UK nuclear weapons data) as published at http://nuclear-weapons.info/images/tna-ab16-4675p63.jpg. This single table summarizes all key tactical and strategic nuclear weapons secret results from 1950s testing! (In order to analyze the warhead pusher thicknesses and very basic schematics from this table it is necessary to supplement it with the 1950s warhead design data declassified in other documents, particularly some of the data from Tom Ramos and Chuck Hansen, as quoted in some detail below.) The data on the mass of special nuclear materials in each of the different weapons argues strongly that the entire load of Pu239 and U235 in the 1.1 megaton B28 was in the primary stage, so that weapon could not have had a fissile spark plug in the centre let alone a fissile ablator (unlike Teller's Sausage design of 1951), and so the B28 it appears had no need whatsoever of a beryllium neutron radiation shield to prevent pre-initiation of the secondary stage prior to its compression (on the contrary, such neutron exposure of the lithium deuteride in the secondary stage would be VITAL to produce some tritium in it prior to compression, to spark fusion when it was compressed). Arnold's book indeed explains that UK AWE physicists found the B28 to be an excellent, highly optimised, cheap design, unlike the later W47 which was extremely costly. The masses of U235 and Li6 in the W47 shows the difficulties of trying to maintain efficiency while scaling down the mass of a two-stage warhead for SLBM delivery: much larger quantities of Li6 and U235 must be used to achieve a LOWER yield! To achieve thermonuclear warheads of low mass at sub-megaton yields, both the outer bomb casing and the pusher around the the fusion fuel must be reduced:
"York ... studied the Los Alamos tests in Castle and noted most of the weight in thermonuclear devices was in their massive cases. Get rid of the case .... On June 12, 1953, York had presented a novel concept ... It radically altered the way radiative transport was used to ignite a secondary - and his concept did not require a weighty case ... they had taken the Teller-Ulam concept and turned it on its head ... the collapse time for the new device - that is, the amount of time it took for an atomic blast to compress the secondary - was favorable compared to older ones tested in Castle. Brown ... gave a female name to the new device, calling it the Linda." - Dr Tom Ramos (Lawrence Livermore National Laboratory nuclear weapon designer), From Berkeley to Berlin: How the Rad Lab Helped Avert Nuclear War, Naval Institute press, 2022, pp137-8. (So if you reduce the outer casing thickness to reduce warhead weight, you must complete the pusher ablation/compression faster, before the thinner outer casing is blown off, and stops reflecting/channelling x-rays on the secondary stage. Making the radiation channel smaller and ablative pusher thinner helps to speed up the process. Because the ablative pusher is thinner, there is relatively less blown-off debris to block the narrower radiation channel before the burn ends.)
"Brown's third warhead, the Flute, brought the Linda concept down to a smaller size. The Linda had done away with a lot of material in a standard thermonuclear warhead. Now the Flute tested how well designers could take the Linda's conceptual design to substantially reduce not only the weight but also the size of a thermonuclear warhead. ... The Flute's small size - it was the smallest thermonuclear device yet tested - became an incentive to improve codes. Characteristics marginally important in a larger device were now crucially important. For instance, the reduced size of the Flute's radiation channel could cause it to close early [with ablation blow-off debris], which would prematurely shut off the radiation flow. The code had to accurately predict if such a disaster would occur before the device was even tested ... the calculations showed changes had to be made from the Linda's design for the Flute to perform correctly." - Dr Tom Ramos (Lawrence Livermore National Laboratory nuclear weapon designer), From Berkeley to Berlin: How the Rad Lab Helped Avert Nuclear War, Naval Institute press, 2022, pp153-4. Note that the piccolo (the W47 secondary) is a half-sized flute, so it appears that the W47's secondary stage design miniaturization history was: Linda -> Flute -> Piccolo:
"A Division's third challenge was a small thermonuclear warhead for Polaris [the nuclear SLBM submarine that preceeded today's Trident system]. The starting point was the Flute, that revolutionary secondary that had performed so well the previous year. Its successor was called the Piccolo. For Plumbbob [Nevada, 1957], the design team tested three variations of the Piccolo as a parameter test. One of the variants outperformed the others ... which set the stage for the Hardtack [Nevada and Pacific, 1958] tests. Three additional variations for the Piccolo ... were tested then, and again an optimum candidate was selected. ... Human intuition as well as computer calculations played crucial roles ... Finally, a revolutionary device was completed and tested ... the Navy now had a viable warhead for its Polaris missile. From the time Brown gave Haussmann the assignment to develop this secondary until the time they tested the device in the Pacific, only 90 days had passed. As a parallel to the Robin atomic device, this secondary for Polaris laid the foundation for modern thermonuclear weapons in the United States." - Dr Tom Ramos (Lawrence Livermore National Laboratory nuclear weapon designer), From Berkeley to Berlin: How the Rad Lab Helped Avert Nuclear War, Naval Institute press, 2022, pp177-8. (Ramos is very useful in explaining that many of the 1950s weapons with complex non-spherical, non-cylindrical shaped primaries and secondaries were simply far too complex to fully simulate on the really pathetic computers they had - Livermore got a 4,000 vacuum tubes-based IBM 701 with 2 kB memory in 1956, AWRE Aldermaston in the Uk had to wait another year for theirs - so they instead did huge numbers of experimental explosive tests. For instance, on p173, Ramos discloses that the Swan primary which developed into the 155mm tactical shell, "went through over 100 hydrotests", non-nuclear tests in which fissile material is replaced with U238 or other substitutes, and the implosion is filmed with flash x-ray camera systems.)
"An integral feature of the W47, from the very start of the program, was the use of an enriched uranium-235 pusher around the cylindrical secondary." - Chuck Hansen, Swords 2.0, p. VI-375 (Hansen's source is his own notes taken during a 19-21 February 1992 nuclear weapons history conference he attended; if you remember the context, "Nuclear Glasnost" became fashionable after the Cold War ended, enabling Hansen to acquire almost unredacted historical materials for a few years until nuclear proliferation became a concern in Iraq, Afghanistan, Iran and North Korea). The key test of the original (Robin primary and Piccolo secondary) Livermore W47 was 412 kt Hardtack-Redwood on 28 June 1958. Since Li6D utilized at 100% efficiency would yield 66 kt/kg, the W47 fusion efficiency was only about 6%; since 100% fission of u235 yields 17 kt/kg, the W47's Piccolo fission (the u235 pusher) efficiency was about 20%; the comparable figures for secondary stage fission and fusion fuel burn efficiencies in the heavy B28 are about 7% and 15%, respectively:
ABOVE: the heavy B28 gave a very "big bang for the buck": it was cheap in terms of expensive Pu, U235 and Li6, and this was the sort of deterrent which was wanted by General LeMay for the USAF, which wanted as many weapons as possible, within the context of Eisenhower's budgetary concerns. But its weight (not its physical size) made it unsuitable for SLBM Polaris warheads. The first SLBM warhead, the W47, was almost the same size as the B28 weapon package, but much lighter due to having a much thinner "pusher" on the secondary, and casing. But this came at a large financial cost in terms of the quantities of special nuclear materials required to get such a lightweight design to work, and also a large loss of total yield. The fusion fuel burn efficiency ranges from 6% for the 400 kt W47 to 15% for the 1.1 megaton B28 (note that for very heavy cased 11-15 megaton yield tests at Castle, up to 40% fusion fuel burn efficiency was achieved), whereas the secondary stage ablative pusher fission efficiency ranged from 7% for a 1.1 inch thick natural uranium (99.3% U238) ablator to 20% for a 0.15 inch thick highly enriched oralloy (U235) ablator. From the brief description of the design evolution given by Dr Tom Ramos (Lawrence Livermore National Laboratory), it appears that when the x-ray channelling outer case thickness of the weapon is reduced to save weight, the duration of the x-ray coupling is reduced, so the dense metal pusher thickness must be reduced if the same compression factor (approximately 20) for the secondary stage is to be accomplished (lithium deuteride, being of low density, is far more compressable by a given pressure, than dense metal). In both examples, the secondary stage is physically a boosted fission stage. (If you are wondering why the hell the designers don't simply use a hollow core U235 bomb like Orange Herald instead of bothering with such inefficient x-ray coupled two-stage designs as these, the answer is straightforward: the risk of large fissile core meltdown by neutrons Moscow ABM defensive nuclear warheads, neutron bombs.)
The overall weight of the W47 was minimized by replacing the usual thick layer of U238 pusher with a very thin layer of fissile U235 (supposedly Teller's suggestion), which is more efficient for fission, but is limited by critical mass issues. The W47 used a 95% enriched Li6D cylinder with a 3.8mm thick U235 pusher; the B28 secondary was 36% enriched Li6D, with a very heavy 3cm thick U238 pusher. As shown below, it appears the B28 was related to the Los Alamos clean design of the TX21C tested as 95% clean 4.5 megatons Redwing-Navajo in 1956 and did not have a central fissile spark plug. From the declassified fallout composition, it is known the Los Alamos designers replaced the outer U238 pusher of Castle secondaries with lead in Navajo. Livermore did the same for their 85% clean 3.53 megatons Redwing-Zuni test, but Livermore left the central fission spark plug, which contributed 10% of its 15% fission yield, instead of removing the neutron shield, using foam channel filler for slowing down the x-ray compression, and thereby using primary stage neutrons to split lithium-6 giving tritium prior to compression. Our point is that Los Alamos got it wrong in sticking too conservatively to ideology: for clean weapons they should have got rid of the dense lead pusher and gone for John H. Nuckolls idea (also used by Fuchs in 1946 and the Russians in 1955 and 1958) of a low-density pusher for isentropic compression of low-density fusion fuel. This error is the reason why those early cleaner weapons were extremely heavy due to unnecessary 2" thick lead or tungsten pushers around the fusion fuel, which massively reduced their yield-to-weight ratios, so that LeMay rejected them!
Compare these data for the 20 inch diameter, 49 inch, 1600 lb, 1.1 megaton bomb B28 to the 18 inch diameter, 47 inch, 700 lb, 400 kt Mk47/W47 Polaris SLBM warhead (this is the correct yield for the first version of the W47 confirmed by UK data in Lorna Arnold Britain and the H-bomb 2001 and AB 16/3240; Wikipedia wrongly gives the 600 kt figure in Hansen, which was a speculation or a later upgrade). The key difference is that the W47 is much lighter, and thus suitable for the Polaris SLBM unlike the heavier, higher yield B28. Both B28 and W47 used cylindrical sausages, but they are very different in composition; the B28 used a huge mass of U238 in its ablative sausage outer shell or pusher, while the W47 used oralloy/U235 in the pusher. The table shows the total amounts of Pu, Oralloy (U235), Lithium-6 (excluding cheaper lithium-7, which is also present in varying amounts in different thermonuclear weapons), and tritium (which is used for boosting inside fissile material, essentially to reduce the amount of Pu and therefore the vulnerability of the weapon to Russian enhanced neutron ABM warhead meltdown). The B28 also has an external dense natural U (99.3% U238) "ablative pusher shell" whose mass is not listed in this table. The table shows that the 400 kt W47 Polaris SLBM warhead contains 60 kg of U235 (nearly as much as the 500 kt pure fission Mk18), which is in an ablative pusher shell around the lithium deuteride, so that the cylinder of neutron-absorbing lithium-6 deuteride within it keeps that mass of U235 subcritical, until compressed. So the 400 kt W47 contains far more Pu, U235, Li6 and T than the higher yield 1.1 megaton B28: this is the big $ price you pay for reducing the mass of the warhead; the total mass of the W47 is reduced to 44% of the mass of the B28, since the huge mass of cheap U238 pusher in the B28 is replaced by a smaller mass of U235, which is more efficient because (as Dr Carl F. Miller reveals in USNRDL-466, Table 6), about half of the neutrons hitting U238 don't cause fission but instead non-fission capture reactions which produce U239, plus the n,2n reaction that produces U237, emitting a lot of very low energy gamma rays in the fallout. For example, in the 1954 Romeo nuclear test (which, for simplicity, we quote since it used entirely natural LiD, with no expensive enrichment of the Li6 isotope whatsoever), the U238 jacket fission efficiency was reduced by capture as follows: 0.66 atom/fission of U239, 0.10 atom/fission of U237 and 0.23 atom/fission of U240 produced by fission, a total of 0.66 + 0.10 + 0.23 ~ 1 atom/fission, i.e. 50% fission in the U238 pusher, versus 50% non-fission neutron captures. So by using U235 in place of U238, you virtually eliminate the non-fission capture (see UK Atomic Weapons Establishment graph of fission and capture cross-sections for U235, shown below), which roughly halves the mass of the warhead, for a given fission yield. This same principle of using an outer U235/oralloy pusher instead of U238 to reduce mass - albeit with the secondary cylindrical "Sausage" shape now changed to a sphere - applies to today's miniaturised, high yield, low mass "MIRV" warheads. Just as the lower-yield W47 counter-intuitively used more expensive ingredients than the bulkier higher-yield B28, modern compact, high-yield oralloy-loaded warheads literally cost a bomb, just to keep the mass down! There is evidence Russia uses alternative ideas.
This is justified by the data given for a total U238 capture-to-fission ratio of 1 in the 11 megaton Romeo test and also the cross-sections for U235 capture and fission on the AWE graph for relevant neutron energy range of about 1-14 Mev. If half the neutrons are captured in U238 without fission, then the maximum fission yield you can possibly get from "x" kg of U238 pusher is HALF the energy obtained from 100% fission of "x" kg of U238. Since with U238 only about half the atoms can undergo fission by thermonuclear neutrons (because the other half undergo non-fission capture), the energy density (i.e., the Joules/kg produced by the fission explosion of the pusher) reached by an exploding U238 pusher is only half that reached by U235 (in which there is less non-fission capture of neutrons, which doubles the pusher mass without doubling the fission energy release). So a U235 pusher will reach twice the temperature of a U238 pusher, doubling its material heating of fusion fuel within, prolonging the fusion burn and thus increasing fusion burn efficiency. 10 MeV neutron energy is important since it allows for likely average scattering of 14.1 MeV D+T fusion neutrons and it is also the energy at which the most important capture reaction, the (n,2n) cross-section peaks for both U235 (peak of 0.88 barn at 10 Mev) and U238 (peak of 1.4 barns at 10 Mev). For 10 Mev neutrons, U235 and U238 have fission cross-sections of 1.8 and 1 barn, respectively. For 14 Mev neutrons, U238 has a (n,2n) cross section of 0.97 barn for U237 production. So ignoring non-fission captures, you need 1.8/1 = 1.8 times greater thickness of pusher for U238 than for U235, to achieve the same amount of fission. But this simple consideration ignores the x-ray ablation requirement of the explosing pusher, so there are several factors requiring detailed computer calculations, and/or nuclear testing.
Note: there is an extensive collection of declassified documents released after Chuck Hansen's final edition, Swords 2.0, which are now available at https://web.archive.org/web/*/http://www.nnsa.energy.gov/sites/default/files/nnsa/foiareadingroom/*, being an internet-archive back-up of a now-removed US Government Freedom of Information Act Reading Room. Unfortunately they were only identified by number sequence, not by report title or content, in that reeding room, and so failed to achieve wide attention when originally released! (This includes extensive "Family Committee" H-bomb documentation and many long-delayed FOIA requests submitted originally by Hansen, but not released in time for inclusion in Swords 2.0.) As the extract below - from declassified document RR00132 - shows, some declassified documents contained very detailed information or typewriter spaces that could only be filled by a single specific secret word (in this example, details of the W48 linear implosion tactical nuclear warhead, including the fact that it used PBX9404 plastic bonded explosive glued to the brittle beryllium neutron reflector around the plutonium core using Adiprene L100 adhesive!).
ABOVE: Declassified data on the radiation flow analysis for the 10 megaton Mike sausage: http://nnsa.energy.gov/sites/default/files/nnsa/foiareadingroom/RR00198.pdf Note that the simplistic "no-go theorem" given in this extract, against any effect from varying the temperature to help the radiation channelling, was later proved false by John H. Nuckolls (like Teller's anti-compression "no-go theorem" was later proved false), since lowered temperature delivers energy where it is needed while massively reducing radiation losses (which go as the fourth power of temperature/ x-ray energy in kev).
ABOVE: Hans A. Bethe's disastrous back-of-the-envelope nonsense "non-go theorem" against lithium-7 fission into tritium by 14.1 Mev D+T neutrons in Bravo (which contained 40% lithium-6 and 60% lithium-7; unnecessarily enriched - at great expense and effort - from the natural 7.42% lithum-6 abundance). It was Bethe's nonsense "physics" speculation, unbacked by serious calculation, who caused Bravo to go off at 2.5 times the expected 6 megatons and therefore for the Japanese Lucky Dragon tuna trawler crew in the maximum fallout hotspot area 80 miles downwind to be contaminated by fallout, and also for Rongelap's people to be contaminated ("accidents" that inevitably kickstarted the originally limited early 1950s USSR funded Communist Party anti-nuclear deterrence movements in the West into mainstream media and thus politics). There was simply no solid basis for assuming that the highly penetrating 14.1 Mev neutrons would be significantly slowed by scattering in the fuel before hitting lithium-7 nuclei. Even teller's 1950 report LA-643 at page 17 estimated that in a fission-fusion Alarm Clock, the ratio of 14 Mev to 2.5 Mev neutrons was 0.7/0.2 = 3.5. Bethe's complacently bad guesswork-based physics also led to the EMP fiasco for high altitude bursts, after he failed to predict the geomagnetic field deflection of Compton electrons at high altitude in his secret report “Electromagnetic Signal Expected from High-Altitude Test”, Los Alamos report LA-2173, October 1957, Secret. He repeatedly caused nuclear weapons effects study disasters. For the true utility of lithium-7, which is actually BETTER than lithum-6 at tritium production when struck by 14.1 Mev D+T fusion neutrons, and its consequences for cheap isentropically compressed fusion capsules in Russian neutron bombs, please see my paper here which gives a graph of lithium isotopic cross section versus neutron energy, plus the results when Britain used cheap lithium-7 in Grapple Y to yield 3 megatons (having got lower yields with costly lithium-6 in previous tests!).
Above: Edward Leader-Williams on the basis for UK civil defence shelters in SECRET 1949 Royal Society's London Symposium on physical effects of atomic weapons, a study that was kept secret by the Attlee Government and subsequent UK governments, instead of being openly published to enhance public knowledge of civil defence effectiveness against nuclear attack. Leader-Williams also produced the vital civil defence report seven years later (published below for the first time on this blog), proving civil defence sheltering and city centre evacuation is effective against 20 megaton thermonuclear weapons. Also published in the same secret symposium, which was introduced by Penney, was Penney's own Hiroshima visit analysis of the percentage volume reduction in overpressure-crushed empty petrol cans, blueprint containers, etc., which gave a blast partition yield of 7 kilotons (or 15.6 kt total yield, if taking the nuclear blast as 45% of total yield, i.e. 7/0.45 = 15.6, as done in later AWRE nuclear weapons test blast data reports). Penney in a 1970 updated paper allowed for blast reduction due to the damage done in the city bursts.
Russian propagandists are discussing the best way to scare the West - testing a nuclear Tsar Bomb or checking bomb shelters. pic.twitter.com/qWCaxjvfM8
— TheKremlinYap (@TheKremlinYap) October 4, 2023
Nuclear saber-rattling from Russian propagandists. They think tactical nuclear weapons aren't enough, and strategic ones should be used.
— Anton Gerashchenko (@Gerashchenko_en) September 29, 2023
Russia has been very active with its nuclear rhetoric recently. pic.twitter.com/1glutLoeqV
Review of Peter Kuran's excellent "Neutron Bomb Movie".
— nukegate.org (@Nukegate) September 29, 2023
Below is a brief clip for review purposes from a longer newsreel of President Eisenhower, enthusiastically promoting the 96% clean fusion Poplar nuclear test (detonated 12 July 1958). On 30 October 1962, Kennedy tested… pic.twitter.com/y4QpR5eCum
Attention, Great Britain!
— Anton Gerashchenko (@Gerashchenko_en) September 13, 2023
Threats to blow up British nuclear facilities from a Russian propagandist. pic.twitter.com/VGX4pjSz8A
ABOVE: The British government has now declassified detailed summary reports giving secret original nuclear test data on the EMP (electromagnetic pulse) damage due to numerous nuclear weapons, data which is still being kept under wraps in America since it hasn't been superseded because Western atmospheric nuclear tests were stopped late in 1962 and never resumed - even though the Russians have even more extensive data - completely debunking Glasstone and Dolan's disarmament propaganda nonsense in the 1962, 1964 and 1977 Effects of Nuclear Weapons which ignores EMP piped far away from low altitude nuclear tests by power and communications cables and falsely claims instead that such detonations don't produce EMP damage outside the 2psi blast radius! For a discussion of the new data and also a link to the full 200+ pages version (in addition to useful data, inevitably like all official reports it also contains a lot of "fluff" padding), please see the other (physics) site: https://nige.wordpress.com/2023/09/12/secret-emp-effects-of-american-nuclear-tests-finally-declassified-by-the-uk-and-at-uk-national-archives/ (by contrast, this "blogspot" uses old non-smartphone proof coding, no longer properly indexed any long longer by "google's smartphone bot"). BELOW: declassified British nuclear war planning blast survival data showing that even without special Morrison table shelters, the American assumption that nobody can survive in a demolished house is false, based on detailed WWII British data (the majority of people in houses flattened within 77 ft from V1 Nazi cruise missiles survived!), and secret American reports (contradicting their unclassified propaganda) proved that blast survival occurred at 16 psi overpressure in Hiroshima's houses, e.g. see limited distribution Dirkwood corp DC-P-1060 for Hiroshima, also the secret 1972 Capabilities of Nuclear Weapons DNA-EM-1 table 10-1, and WWII report RC-450 table 8.2, p145 (for determining survival of people sheltered in brick houses, the WWII A, B, C, and D damage versus casualty data from V1 blast was correlated to similar damage from nuclear blast as given Glasstone's 1957 Effects of Nuclear Weapons page 249, Fig. 6.41a, and page 109 Fig. 3.94a, which show that A, B, C, and D damage to brick houses from nuclear weapons occur at peak overpressures of 9, 6, 3 and 0.5 psi, respectively; the longer blast from higher yields blows the debris over a wider area, reducing the load per unit area falling on to people sheltered under tables etc), and the declassified UK government assessment of nuclear terrorist attack on a port or harbour, as well as the confidential classified UK Government analysis of the economic and social effects from WWII bombing (e.g. the recovery times for areas as a function of percentage of houses destroyed):
Note: the DELFIC, SIMFIC and other computer predicted fallout area comparisons for the 110 kt Bikini Atoll Castle-Koon land surface burst nuclear test are false since the distance scale of Bikini Atoll is massively exaggerated on many maps, e.g. in the Secret January 1955 AFSWP "Fall-out Symposium", the Castle fallout report WT-915, and the fallout patterns compendium DASA-1251! The Western side of the Bikini Atoll reef is at 165.2 degrees East, while the most eastern island in the Bikini Atoll, Enyu, is at 165.567 degrees East: since there are 60 nautical miles per degree by definition, the width of Bikini Atoll is therefore (165.567-165.2)(60) = 22 nautical miles, approximately half the distance shown in the Castle-Koon fallout patterns. Since area is proportional to the square of the distance scale, this constitutes a serious exaggeration in fallout casualty calculations, before you get into the issue of the low energy (0.1-0.2 MeV) gamma rays from neutron induced Np239 and U237 in the fallout enhancing the protection factor of shelters (usually calculated assuming hard 1.17 and 1.33 MeV gamma rads from Co60), during the sheltering period of approximately 1-14 days after detonation.
Unofficial Russian video on the secret Russian nuclear shelters from Russian Urban Exploration, titled "Проникли на секретный Спецобъект Метро!" = "We infiltrated a secret special facility of the Metro!":
ABOVE: Moscow Metro and Metro-2 (secret nuclear subway) horizonially swinging blast doors take only 70 seconds to shut, whereas their vertically rising blast doors take 160 seconds to shut; both times are however far shorter than the arrival time of Western ICBMs or even SLBMs which take 15-30 minutes by which time the Russian shelters are sealed from blast and radiation! In times of nuclear crisis, Russia planned to evacuate from cities those who could not be sheltered, and for the remainder to be based in shelters (similarly to the WWII British situation, when people slept in shelters of one kind or another when there was a large risk of being bombed without notice, particularly in supersonic V2 missile attacks where little warning time was available).

ABOVE: originally SECRET diagrams showing the immense casualty reductions for simple shelters and local (not long distance as in 1939) evacuation, from a UK Home Office Scientific Advisers’ Branch report CD/SA 72 (UK National Archives document reference HO 225/72), “Casualty estimates for ground burst 10 megaton bombs”, which exposed the truth behind UK Cold War civil defence (contrary to Russian propaganda against UK defence, which still falsely claims there was no scientific basis for anything, playing on the fact the data was classified SECRET). Evacuation plus shelter eliminates huge casualties for limited attacks; notice that for the 10 megaton bombs (more than 20 times the typical yield of today’s MIRV compact warheads!), you need 20 weapons, i.e. a total of 10 x 20 = 200 megatons, for 1 million killed, if civil defence is in place for 45% of people to evacuate a city and the rest to take shelter. Under civil defence, therefore, you get 1 million killed per 200 megatons. This proves that civil defence work to make deterrence more credible in Russian eyes. For a discussion of the anti-civil defence propaganda scam in the West led by Russian agents for Russian advantage in the new cold war, just read posts on this blog started in 2006 when Putin's influence became clear. You can read the full PDF by clicking the link here. Or see the files here.
ABOVE: the originally CONFIDENTIAL classified document chapters of Dr D.G. Christopherson’s “Structural Defence 1945, RC450”, giving low cost UK WWII shelter effectiveness data, which should also have been published to prove the validity of civil defence countermeasures in making deterrence of future war more credible by allowing survival of “demonstration” strikes and “nuclear accidents / limited wars” (it’s no use having weapons and no civil defence, so you can’t deter aggressors, the disaster of Munich appeasement giving Hitler a green light on 30 September 1938, when Anderson shelters were only issued the next year, 1939!). For the original WWII UK Government low cost sheltering instruction books issued to the public (for a small charge!) please click here (we have uploaded them to internet archive), and please click here for further evidence for the effectiveness of indoor shelters during WWII from Morrison shelter inventor Baker's analysis, please click here (he titled his book about WWII shelters "Enterprise versus Bureaucracy" which tells you all you need to know about the problems his successful innovations in shelter design experienced; his revolutionary concept was that the shelter should be damaged to protect the people inside because of the vast energy absorption soaked up in the plastic deformation of steel - something which naive fools can never appreciate - by analogy, if your car bumper is perfectly intact after impact you're unlikely to be because it has not absorbed the impact energy which has been passed on to you!). We have also placed useful declassified UK government nuclear war survival information on internet archive here and here. There is also a demonstration of how proof-tested WWII shelters were tested in 1950s nuclear weapon trials and adapted for use in Cold War nuclear civil defence, here, thus permanently debunking the somewhat pro-dictatorship/anti-deterrence Jeremy Corbyn/Matthew Grant/Duncan Campbell anti-civil defence propaganda rants which pretend to to based on reality, but obviously just ignore the hard, yet secret, nuclear testing facts upon which UK government civil defence was based as my father (a Civil Defence Corps instructor) explained here back in 2006. The reality is that the media follows herd fashion to sell paper/airtime; it doesn't lead it. This is why it backed Nazi appeasement (cheering Chamberlain's 1938 handshakes with Hitler for instance) and only switched tune when it was too late to deter Nazi aggression in 1939; it made the most money that way. We have to face the facts!
ABOVE: British 1959 summary of the effects of nuclear weapons on military equipment, based on extensive British nuclear test data. This information has been declassified in the 1959 book An introduction to nuclear weapon effects (UK War Office WO Code: 9612), available in the UK National Archives as document WO 279/476 - see https://discovery.nationalarchives.gov.uk/details/r/C1806524 - it is also well known to the Russians, Chinese et al., who have conducted such tests, yet is not included in the American Glasstone and Dolan nuclear effects bible: this is the key data for credibly deterring the invasions behind world wars. Without the full nuclear weapons effects facts being in the public arena, ill informed anti-nuclear people can campaign to disarm Western tactical nuclear weapons, thus enabling Putin to invade Ukraine and other countries. The photo below of the 1955 Nevada tested suitcase bomb Cleo II (Cleo II was tested as 2 kt Teapot-Post on 9 April 1955, 34.2" long, weight 322 lb) being used as a lunch table in the back of a station waggon on route to the bomb tower, is from Tom Ramos's 2022 book "How the Rad Lab helped avert nuclear war", which explains Cleo's linear implosion shape was too complex to simulate on computers, so Foster had to use many non-nuclear explosive "hydrotests" using depleted uranium cores: "The committee noted the multidimensionality of the Cleo made it difficult to model on a computer; its design pushed into areas of physics not well understood." Ramos also writes on pages 118-121 (his end notes say he read the secret test notes on this to confirm it) that Edward Teller's Lawrence Livermore Laboratory's 110 kt Castle-Koon test failed to yield the desired 1 megaton because the (rival) Los Alamos primary fission stage used in it yielded only half the x-rays needed to compress it: "Montgomery Johnson ... determined the calculations of energy flowing throughout the device had been wrong ... comparisons of the radiative transport calculations with measurements of the output of the Los Alamos primary had shown they differed by a factor of two. The device's design had been based on those calculations..."
ABOVE: CIA-declassified testimony from 1985 (linked here) states that Russia built 800-1,500 relocation shelters for government officials, in addition to public basement shelters and subway shelters and evacuation/dispersal plans for a crisis (in WWII, the Russian government relocated from Moscow to Kuybishev, where there is now a deep shelter under dry soft rock). The U.S. Department of Defense's April 1988 edition of Soviet Military Power: An Assessment of the Threat at pages 59-61 adds that Russia built secret subway lines, nicknamed "Metro-2", extending from the Kremlin in Moscow out to relocation shelters 60 km away such as that at Sharapovo, 60 km South of Moscow. (See also the map of these secret railway line on page 43 of DTIC report ADA243946, linked here.) Bruce Blair in his 1993 Brookings Institution book, The Logic of Accidental Nuclear War, pages 133-140, compares this data with other sources, and analyses the implications in terms of the massive exaggerations by Glasstone and Dolan on crater/ground shock effects to buried shelters. E.g., Blair states at pages 134-140 that there is another shelter at Chekhov, also 60 km from the Kremlin, but West of Sharapovo:
ABOVE: Blast door at Komsomolskaya ("Комсомо́льская") Metro Station on the Koltsevaya line, Krasnoselsky District, Central Administrative Okrug, Moscow (average depth of Moscow metro is 45 metres; this station is at 37 metres depth and so provides excellent nuclear effects resistance at very high peak overpressures and radiation fields). Notice the curved track on the floor on the the blast door on the right would be swung shut by a hydraulic ram (located behind it!). The blast doors and their hydraulic mechanisms are similar to the silo blast doors that protect large ICBMs from several thousand psi peak overpressure at ground zero, although the shelters have several blast doors, and giving greater protection. It is a nicely camouflaged Russian civil defense system! (Photo source: https://www.oneman-onemap.com/en/2017/08/08/the-moscow-metro/ ) Bruce Blair, Logic of Accidental Nuclear War (pages 134-140):
"These exurban deep underground command posts were connected to the deep underground post at the Kremlin by a special subway line. Two other special subway lines branched out from the Kremlin. One wound through the Ramenki area deep underground command post southwest of Moscow State University, and on to exurban deep posts farther to the South West of the city. The other ran 25 km East to a deep underground complex housing the national air defense HQ. ... the most heavily fortified allegedly could withstand blast overpressures as high as several thousand pounds per square inch. ... a very deep command centre beneath the Kremlin ... in the early 1980s earned a Lenin Prize for former general secretary Chernenko. The largest underground complex ... was situated at Ramenki at an estimated depth of 650-1,000 feet. It could accommodate 10,000 people. ... Recently the U.S. Department of Defense reviewed the pertinent historical evidence gathered during nuclear tests and developed new models of the vulnerability of underground structures to nuclear explosions. These calculations differed substantially from those derived from earlier models. ... the dimensions of a crater produced by a nuclear explosion were estimated to be considerably smaller than previously thought. ... the radius of a crater produced by a 1 Mt nuclear explosion on the surface of wet soil [crater radii will be only 58.3% this size in Moscow's wet soft rock, which is tougher to crater than wet soil] would be 651 feet according to the old formula, whereas the new formula estimated the radius to be 394 feet. ... A 9 Mt bomb would have produced a crater radius of 590 feet in wet soil [according to the new formula] ... Under the new formula the pertinent calculations for this location's [the shelter at Kuybishev where Stalin retreated in WWII] geological composition (dry soft rock, according to U.S. analysts) indicate a crater radius of only 180 feet for a 1 Mt weapon, or 262 feet for a 9 Mt weapon. ... on the old formula ... crater radius would have been 485 and 937 feet for 1 Mt and 9 Mt..."
Chapter 5 of Blair's book summarises the intelligence on the best known major Russian nuclear war exercises, those of 1984 and 1988. The 1984 Russian nuclear war exercise assumed that a conventional East-West war lasted for just 10 days before escalating, while the 1988 exercise assumed that it lasted 30 days before escalating to nuclear strikes in which Russia fired land based missiles from silos 9 minutes before U.S. ICBMs arrived to blow up the empty Russian silos. (So in any likely major nuclear war scenario of escalation from a major East-West conventional war, Russia was intending to switch to launch-on-warning to prevail. This policy, Blair states on page 196 of Chapter 6, "Launch on Warning", was developed by Russia in the February 1955 issue of its secret Military Thought journal, as a countermeasure to prevent the success of a surprise strike during a crisis.) Blair also on page 26 quotes Henry Kissenger's advice that in a crisis you should escalate "rapidly and brutally to the point where the opponent can no longer afford to experiment" (quotation source is Kissinger's White House Years, 1979, p622). Blair comments (based on the experiences of the failure of gradual escalations prior to WWI and WWII by appeasers and misinformed idealists): "Henry Kissinger argued that what seems balanced and safe in a crisis is often the most risky because because a too temperate, deliberate, and predictable course allows the adversary to match every move, thereby prolonging the conditions of inherent risk. His prescription was to exploit the adversary's reluctance to play nuclear roulette ... the crisis may be brought to a quick and favourable resolution. Kissinger practised this philosophy of crisis management during the 1973 Middle East crisis by declaring a global U.S. nuclear alert in the hope that it would deter the Soviets from intervening unilaterally to save the trapped Egyptian army ... a ploy to convince the Soviets of our willingness, if necessary, to run a risk of nuclear war in order to prevail."
This is relevant to the UK Government policy in August 1914 and from 1933-39, when its "speak softly and carry a big stick" diplomatic policy (a phrase mentioned by President Ted Roosevelt as being a useful West African proverb) failed to deter world wars. Speaking softly undermined the credibility of the big stick for deterrence: the opponent has to believe it to be a credible threat, which means you must convince your opponent of your desire to use the stick to enforce your will. In the end, Britain in both cases declared war first, after convincing its opponent that it was committed to peaceful coexistence. Being nice to a monster may turn the monster "nice" in the fairy tales of "arms controllers and disarmers", but in the real world it encourages and rewards aggression. Anyone pointing out this fact of human nature was secretly attacked by underhand methods by Chamberlain's thugs, e.g. pressure on the publisher of Popular Flying resulted in editor Johns being fired in 1939 for writing editorials critical of appeasement and efforts were made to de-select Winston Churchill, MP. The pro-Chamberlain lying propaganda continues, driven by disarmament liars, who believe in lying about anything, particularly civil defense and weapons effects, to get peace at the price of despotic genocide and slavery, the Pyrrhic "victory" of fools.
Above (12 June 2023 update): please see https://twitter.com/Nukegate/ for recent escalation news. Bignose (yours truly) has added some videos on the need for activism to get the word out urgently over the crisis. Note that the present hybrid war situation has some elements in common with situations in early 1939 (when Germany had partially but not completely invaded its neighbour Czechoslovakia) and the situation in mid 1914, when the UK government was also deluding itself by focussing on trivial domestic affairs, rather than on the so-called squabbles in faraway lands between people of whom we couldn't care less. Particularly, it wasn't really Churchill's brain that smashed the Nazis, but rather the 10,000 staff at Bletchley Park's Enigma codebreakers and later in the war colossus, the first programmable computer, used to find cypher keys to the more difficult Fish code (the higher level Nazi code than the better known Enigma code); until the enemy codes were deciphered, upto El-Alamein in 1942, Britain lost every battle (and just managed to fend off enemy invasion with the Dunkirk Evacuation and the Battle of Britain 1940) but afterwards - forewarned and forearmed by the secret decoding of classified Nazi radio telex signals - the West won victory after victory, a fact suppressed from history due to official secrecy until 1974 (because Enigma machines were sold to governments around the world after WWII and we continued to keep secret the fact we could decode them due to the need to fight the Cold War), so all histories until 1974 are corrupt, and this factor is still being falsely used to give both Monty and Churchill an exaggerated aura of genius which is more honestly ascribed to a programmable 5-ton, 100-logic gate vacuum tubes machine, plus American lend-lease and then entry into WWII after Pearl Harbor. There are horrifying lessons here than we need to face up to squarely, not through the rose-tinted specs of historically corrupt nostalgia! We are again in potential pre-war era, and time to prepare to survive and prevail may again be running out.
Western tactical neutron bombs were disarmed after Russian propaganda lie. Russia now has over 2000 - Russian propaganda and coercion of the Western nuclear disarmers and its Marx media leads to mass murder with nuclear weapons becoming a repeat of the 1920s-1930s BBC "news" gas war liars led by Professor Philip Noel-Baker (who repeated the same genocidal disarmament "trick" against the neutron bomb in the cold war, as we will show later in this post, below) to shut down credible deterrence and suck up to lying mass-murdering dictators promising heaven on earth. By the way, the military casualty toll for the Ukraine war is only a small fraction of the total murdered due to the Western ideologues decision to ensure Ukraine's failure to quickly win the war by only escalating incrementally to suck Putin into WW3, precisely Chamberlain's half-witted approach under pressure from similar liars in the 30s (a deliberate Tom Schelling "play war as a chess game, and don't escalate to win - reverse the long established rules of war and win a Nobel prize in economics for bankrupting humanity), the now "mainstream" fake ideology approach as used by lefty militarists like Ike, Johnson and Biden to lose in Korea, Vietnam, Afghanistan respectively), due to collateral damage in the form of long-term inflated living costs of heating energy and food in Europe as we predicted in 2014, mass murdering the elderly; something the Yank media like John doesn't seem to give a damn for (this is a 100%-updated re-blog of our 22/02/22 post). Please note that the link to the analysis of the secret USSBS report 92, The Effects of the Atomic Bomb on Hiroshima, Japan (which google fails to appreciate is a report with the OPPOSITE conclusions to the lying unclassified reports and Glasstone's book on fire, is HERE, being part of the internet archive page HERE. If you don't like the plain layout of this blog, you can change it into a "fashionable" one with smaller photos you can't read by adding ?m=1 to the end of the URL, e.g. https://glasstone.blogspot.com/2022/02/analogy-of-1938-munich-crisis-and.html?m=1. See also: War Plan UK.
ABOVE: left-wing Guardian finally reports (better late than never) Russia's cold war Stalinist nuclear shelters (developed from the results of Stalin's nuclear tests, as we will reveal in detail in this blog post, below) are being prepared for WW3 in 2023, but naturally claims it is not for WW3, but merely in case a missile goes astray from Ukraine into Russia (the official "Brezhnev era apparatchik"-line, strike that and replace Brezhnev with Putin): "Although a missile attack deep into Russia is unlikely, bunkers built long ago are being made ready for use.". Our twitter feed, https://twitter.com/Nukegate keeps you informed of the latest Russian TV nuclear war plans and shelter preparations. When Russian shelters are fully ready, we can expect the Ukraine war to escalate rapidly. Yahoo news for instance reports:
"Russia’s Secretly Splurging on Bomb Shelters ‘Everywhere,’ Report Says. The Kremlin has quietly ordered an upgrade to bomb shelters across Russia, according to four former and current Russian officials who spoke with The Moscow Times. “An order was given from Moscow to carry out this work everywhere—inspection and repair,” ... Local authorities have reportedly spent hundreds of millions of rubles on the bomb shelter preparations, which allegedly began in February 2022 after Russia invaded Ukraine. The preparations will reportedly continue this year. And although in some regions authorities have installed signs near the shelters, some authorities have sought to downplay the updates, in an apparent attempt to avoid causing panic. ... Moscow has refused to allow U.S. inspections on its territory since August, and NATO ambassadors said in a statement last week that Russia is failing to comply with its obligations under the New START Treaty. ... Russia accused Ukraine without evidence of preparing a dirty bomb—a weapon with both conventional explosives and radioactive material—as fears mounted that Russian President Vladimir Putin was working to create a justification to use nuclear weapons." Russia's nuclear labs also released the following photo of Western neutron bomb disarmament fanatic Dr Joseph Rotblat patting the Russian nuclear bomb of Russian neutron bomb inventor Dr Boris Litvenko (a war mongering USSR restoration advocate, the guy with big eyebrows on far right). Rotblat is a hater of Western nuclear weapons and Western civil defense, but not Russian.
"Controlling escalation is really an exercise in deterrence, which means providing effective disincentives to unwanted enemy actions. Contrary to widely endorsed opinion, the use or threat of nuclear weapons in tactical operations seems at least as likely to check [as Hiroshima and Nagasaki] as to promote the expansion of hostilities [providing we are not in a situation of Russian biased arms control and disarmament whereby we no tactical weapons while the enemy has over 2000 neutron bombs]." - Bernard Brodie, pvi of "Escalation and the nuclear option", RAND Corp memo RM-5444-PR, June 1965.
ABOVE: neutron bombs alone produce huge deterrent neutron output at low kiloton yields. e.g. 1660 rads/kt at 1 km from a ground burst type 13 neutron bomb on silicate soil compared to merely 0.666 rads for the type 10 low-yield-option of a B61 or W88 bomb with multiple yield options, called "dial-a-yield" (the data above is calculated from the neutron dose equations in EM-1, 1984), the reason being that the low yield option just involves an unboosted fission primary stage (which is too weak without boost gas to compress the secondary stage enough to cause that to explode) and the lithium deuteride in the secondary stage acts as a "neutron sponge" that absorb most of the neutrons from the unboosted primary stage, preventing it from being an efficient source of neutrons, and Northrop's declassified EM-1 says in Table 8.10 that Russia and China - since only Russia and China have neutron bombs since NATO's W79's were disarmed in 1992 by loons - have two types of neutron bomb, a low yield and a high yield version, with yields 1-5 and 5-15 kt, with burst heights of 50-100 and 100-300 m, respectively. I have also put up a video explaining that although Putin and friends are sick loons by our Western standards, ideology and national financial issues may mean he feels - like Hitler in 1939 - impelled try to get allies on board (like Hitler did in getting Stalin to agree to jointly invade Poland in September 1939), to start WW3. I hope I'm wrong! But I remember my boy scout's motto "be prepared" and the old Royal Observer Corps motto "forewarned is forearmed" (both these mottos are anathema to the left, proving them to be right). Also, notice that when Hitler and Stalin invaded Poland in September 1939 according to the secret aggression annex to their joint "non-aggression treaty" of August 1939, Hitler believed that he could avoid WW2 by coercing the UK into a "peace pact" due to the fear of London being bombed. By analogy, if Putin and his potential allies do start WW3, they won't admit they are doing it. They simply declare it is another secret special military operation to coerce Western imperialists into peace, not a deliberate triggering of WW3 (Hitler's ploy to curry favour with his people and maybe even what he believed in his own delusional alternative universe, who knows/cares?).
"3/13/23 NEWSWEEK: "I think that [Putin's] nuclear threat is a real threat," Russian lawmaker Grigory Yavlinsky told Newsweek, echoing Putin's remarks that the warnings are "not a bluff." "It's a real threat. That kind of weapon is such a serious thing...this is not [just] words, this is a real factor, which you have to take into consideration in the current situation. That's it," he said.
NATO REVIEW: "In 2022, the spectre of nuclear weapons use has returned to centre stage in Europe. From the very beginning of Russia’s invasion of Ukraine in February of this year, Russian President Vladimir Putin has brandished his country’s nuclear sword in an attempt to compel Ukraine to capitulate to Russia’s demands and to deter NATO from intervention. This is the most significant attempt at prolonged, consistent, and conscious nuclear coercion against NATO and its partners in almost forty years. We must therefore reflect on Russia’s nuclear coercion with considerable scrutiny. ... With Russia’s arsenal of roughly 2,000 tactical nuclear weapons, the escalatory threat that Russia presents below the strategic nuclear level – that is, in using nuclear weapons with smaller yields and shorter ranges – regrettably forces NATO to meet that threat with its own credible option. ... While NATO issued a new Strategic Concept this past June that highlighted the role of nuclear weapons in Allied deterrence, the document was light on specifics, suggesting that Allies would rely on an “appropriate mix” (para. 20) of nuclear and conventional military systems. As Russia’s military position continues to deteriorate in the face of heroic Ukrainian resistance and international sanctions, and as Moscow becomes increasingly isolated from the international community, it is not difficult to imagine that Putin will begin to turn more frequently and more aggressively to his nuclear signals in order to extract political concessions from the West and Ukraine. Having been maneuvered onto Thomas Schelling’s “slippery slope” of competitive risk-taking, is NATO equipped to respond credibly to Russian threats of nuclear escalation?" (HEY MATE! You guys need plans for more than just "threats"!)
Nuclear weapons have been used again, as threats, and the fascist Russian supporting CND backing media have ironically dismissed them as parlour jokes (unlike the 1962 Cuban missiles crisis, when the USA had a massive superiority for far more credible deterrence than we have today, used by Kennedy in his 22 October TV broadcast to deter the the accidental launching of a single missile from Cuba against any city in the West), so already we are seeing on BBC TV and Russian State TV attempts to deter escalations needed to end the Ukraine war. Russian appeasing or ignorant media is itself being coerced by reality into occasionally allowing hints of realism to enter the public domain, since they'll go under if they keep ignoring it or simply ridiculing it as "unthinkable" and therefore "taboo", inspired by the decades of Moscow's World Peace Council lies (summarised in places like Rhodes' "history" books, Arsenals of Folly and The making of the atomic bomb which lie about nuclear weapons). Here's what to do to immediately kick the crap out and end the Ukraine war: list the conventional megatonnage in each World War, the nuclear equivalent, bearing in mind that effects like blast and radiation areas don't quite scale up directly in proportion to the total energy release, especially for concrete cities where the concrete absorbs radiation and blast energy efficiently as in 1945 Hiroshima (where there were few concrete buildings compared to modern cities, but enough for Penney to determine shielding factors which Glasstone ignored). For example, 2.5 megatons of bombs were dropped in World War II, their average yield being of the order 0.0000001 megaton (0.1 ton), so if we conservatively ignore the cumulative shielding by concrete buildings in a city and use open desert cube-root distance scaling (two-thirds power for damaged or lethal areas) the number of 1 megaton bombs needed to create the same damage (the so-called "equivalent megatonnage") is obviously equal to (2,500,000/0.1)(0.00000012/3) = 539 megaton thermonuclear explosions.
This calculation can be repeated for other wars as a homework exercise, then you should repeat it over again for the much smaller pre-war stockpiles used for "deterrence" before WWI and WWII, and study a recent, honest summary of the cancer data from radiation due to the effects of actual nuclear weapons use in war. This alone gives you a bloody realistic basis to quantitatively grasp the mumbo jumbo words used by bigots to weave their history out of whole cloth. Now you are welcome to argue the toss about the details of accurate energy comparisons: for bigger explosions you people get up to 4.7 seconds per mile distance before the blast arrives to duck and cover from blast winds and flying debris, lacking in lower yield conventional surprise bombings where the damaged area is smaller (the average shock front speed is faster near ground zero in bigger explosions, for example taking 40 seconds to arrive 10 miles from 1 megaton, not 47 seconds). So civil defence makes more sense in nuclear war than in conventional war, although the Vietcong used good tunnel shelters to take over 5,000,000 tons of conventional bombs for victory through survivalism, propaganda in the enemy press, and enemy financial effects since digging holes was cheaper than making dropping bombs, contrary to every taboo ever invented by fascist liars to "disprove civil defence as a joke", as indeed did London in withstanding 12,000 tons of small conventional bombs in the Nazi Blitz without surrender, contrary to PM Chamberlain's prewar lying about such bombs inducing defeatism and surrender (it is equivalent to megatons of nuclear weapons yet had the exactly opposite effect to Chamberlain's lies, which is still ignored due to populist lying about WWI UK civil defence by the anti-civil defence marxist liar Angus Calder in his "People's War", where he promotes, hook-line-sinker the 1930s Marxist "Cambridge Scientists Anti-War Group" lies that bomb shelters and gas masks were just a propaganda ploy of no use whatsoever against bombs, a deception helped by the UK government's deliberate anti-democratic and anti-humanity decison for decades even after WWII - opposed bitterly by my father, Civil Defence Corps instructor John B. Cook - to keep shelter effectiveness data classified "Confidential" in Christopherson's report RC450, "Structural Defence 1945".
But it's not just the UK government keeping the public ignorant of key facts to duplicate the Kremlin's propaganda machine, since President Carter said in his farewell address that nuclear weapons can only possibly be used in an all-out totally disarming war spread across a single afternoon, not a couple of nuclear bombs to escalate and end a long war as happened in Hiroshima and Nagasaki, August 1945. But was he a liar, just ignorant, both? How can "democracy" under such secrecy ever force the military to get real with overwhelming nuclear deterrence to end the slaughter of conventional wars, to stop classifying the truth top secret, when it is known to the enemy, and only the delusional mad Marx media and their fashion duped rivals like "Nukemap guy" (and those who believe him), remain faithful to bigoted nonsense. We'll examine in detail the blast and radiation shielding by concrete cities and their effect on reducing still further the utility of larger explosions, later below.
ABOVE: years ago the Nevada NNSA very kindly and helpfully scanned in the originally "Top Secret" classified report by Walmer E. Strope originally deriving the 25 July 1946 Crossroads-Baker fallout pattern which was later simplified and used in the fallout patterns compendium, DASA-1251 (Baker was 23 kt at a depth of 90 feet in 180 feet of water, within Bikini Lagoon). I put it on Internet Archive for all to use. However, as with so many declassified reports, what you get is possibly a copy-of-a-copy of what is probably a microfiche print-out from a faded microfilm made about 70 years ago, so you can't see details clearly like the ship names. You can get around this with some effort, since other documents such as Shelton's Reflections of a Nuclear Weaponeer, gives maps of the ship arrays in Operation Crossroads. But there is a huge amount of time required to process all the data. Why isn't everything now freely available? What benefit is there to this sort of nonsense? The same secrecy nonsense applies to EMP data:
The Russians were the first to worry about EMP after it was piped into their instruments by 560km of cables at the 1949 RDS-1 nuclear test. The Russian nuclear weaponeer Kompaneets was first to publish the nuclear EMP in unclassified literature, in "Radio emission from an atomic explosion", dated December 1958: http://jetp.ras.ru/cgi-bin/dn/e_008_06_1076.pdf. However, RAND Corp's Gilinsky debunked Kompaneets' peak field approximation in the 4 Jan 1965 Physical Review (v137, ppA50-A55). Russian nuclear tests were much better funded for determining the effects and protective countermeasures than Western tests. The full details of surface burst EMP have been declassified in Northop's 1996 EM-1 summary book and other American and British reports, but as with other effects of nuclear weapons, there is a HUGE amount of attenuation of the EMP by a modern high-rise steel and concrete city:
ABOVE: still suppressed EMP data published by Senator Goldwater (64 Presidential nominee) in 19 September 1963 Senate Congressional Record exposing EMP damage in Las Vegas from 1951 near surface bursts due to cable coupling. Notice that even as late as 1977, the ill informed rubbish in the Glasstone Effects of nuclear weapons claimed that EMP has no effect outside the 2psi blast radius (roughly the deposition region radius with a few thousand v/m EMP field strength) in surface bursts, when in fact, very intense ~100,000 v/m EMP on the cables close to ground zero is simply piped out to enormous distances by conductors in microseconds (before air blast or ground shock can damage them!), so the limiting damage radius for EMP in such bursts depends on the resistance (ohms per metre) of the cables! It doesn't depend on the EMP field strength at the end of the cable where the damage occurs, any more than you have to have a power station on your doorstep to keep your lights on!
ABOVE: the British government's approved chart of nuclear weapons which notes that Russia has kept some nuclear weapons secret and not listed, which is accompanied by a text which seems to be virtually a carbon-copy of Baldwin's government's 1935 announcement of Germany's rearmament threat, complete with the same demented disarmament-ain't-working-as-we-hoped complaint that: "The UK has taken a consistent and leading approach on nuclear disarmament but not all states have followed. ... To help explain how some states are expanding their nuclear capabilities, NATO have prepared this graphic which uses Russia’s expanding arsenal as an example of this trend and compares it with the systems held by the UK and fellow NATO nuclear weapons states France and the United States. It shows that Russia is significantly increasing the variety of nuclear capable weapons that it possesses. This is in contrast to the work that the NATO nuclear weapons states have undergone to reduce and maintain relatively modest arsenals since the Cold War ended. China also continues to modernise and expand its nuclear capabilities. ... It is wrong to say that the UK’s nuclear deterrent is never used. The reality is that it protects us every hour of every day. By providing a credible and effective response option to extreme aggression, our nuclear deterrent reduces the likelihood of such an attack taking place." (No, mate: the point is that we failed to deter the invasion of Belgium in 1914, and of Poland in 1939, leading to World Wars that murdered tens of millions, then we developed tactical nuclear weapons and used them to deter invasions from the 1950s onwards, too late to help Eastern Europe, but "better late than never". Now we have none, due to 1990s disarmament activists being unopposed and using Glasstone's 1977 horseshit non-military lying nuclear effects manual, applying open desert unshielded thermal and blast data falsely to concrete cities that shield effects, instead of giving neutron bomb effects data for invading tanks and troops! We need change tactics urgently or risk costly, bloody escalations.)
Ambiguity. Foreign Secretary Edward Grey's lying "it was the arms race wot done it, honest" excuse after refusing to credibly deter WWI in 1914 - because he wouldn't tell Germany in advance whether the invasion of Belgium would trigger Britain to declare war (the Cabinet couldn't make up its mind until too late to credibly deter Germany), was the ambiguous recipe for arms race-avoiding disaster which Chamberlain and other appeasers followed in the 1930s. Providing that arms industry contracts corruption can be carefully minimised, as in the West in WWII and the Cold War, arms races have historically proved to be far more damaging to dictatorships than to Democracies! You have to escalate an arms race until the opponent is bankrupt, the opposite of 1930s unilateral disarmament which leads to world war and genocide.
Herman Kahn's 1960 RAND Corporation paper P1888-RC, The nature and feasibility of war and deterrence (a summary of a few key point in his book of the same year, "On thermonuclear War", but better organized and briefer) states Malenkov introduced the mutual assured destruction anti-war deterrence concept to Russia, before he was replaced by Khrushchev who took a very different view, repeatedly threatening nuclear war against Eisenhower's defense of West Berlin, even before Russia had the nuclear superiority in clean high neutron output tactical weapons it has today:
"Even mutual belief in the automatic annihilation theory can still lead to trouble; the invitation to blackmail of the Munich type [Hitler threatened retaliation if his invasion of Sudetenland was interferred with in 1938, leading to appeasement which effectively invited him to invade the entirety of Czechoslovakia and then Poland the next year, triggering a world war] ... Would only an insane man initiate a thermonuclear war? ... a war might start as a result of an accident, some miscalculation, or even irresponsible behavior
[EMPHASIS ADDED; Kennedy used Kahn's words here in his May 1961 civil defense fallout shelters implementation speech, and this point about irresponsible behaviour by the Kaiser, Hitler and Stalin in jointly invading Poland from different sides in 1939, the Pearl Harbor attack plan, etc., is also emphasised as the key risk of global nuclear warfare in Sir John Hackett's book The Third World War and is especially relevant to a dictator cornered by financial debt pressures like Hitler, medical issues like Anthony Eden's perforated bowel agony during the Suez Crisis of 1956, Chamberlain's cancer in 1940 which nearly put appeaser Lord Halifax into power instead of gung-ho adventurer Churchill - whose apparent eventual success actually owes a very great deal to Hitler's decision to invade it's partner in the September 1939 Polish invasion, Russia, on 22 June 1941 and then to declare war on America following Pearl Harbor, deciding to follow the terms of his 27 September 1940 Tripartite Pact with Japan; factors that Churchill could not have relied upon when refusing to negotiate with Hitler, and didn't when formulating his contingency plans to move the UK government to Canada in the event of a successful invasion of the UK; the anti-nuclear Russian scam propaganda about "nuclear accidents" are a red herring unless actually deliberate false-flag "sink the Maine" excuses for escalation to try to end the war (if there is a nuclear accident it won't start a war unless it is a contrived plot to do so, as when implementing the Schlieffen Plan in 1914); there is also the continuing debate over whether Stimson was irresponsible in his advice to Truman that Hiroshima and Nagasaki were simply military targets, when they also contained large numbers of civilians, and this issue over the errors in advice even continued when kids were napalmed in the Vietnam war under the supposed control of Kennedy's successor, Democratic President Johnson].
"... Russian civil defense manuals (dated 1958) indicate ... preparation for evacuation for improvised fallout protection ... While this would give us a sort of warning, we might not act on it [if you were US President, would you start WWIII by firing off nuclear missiles to try to stop Russians being evacuated from cities, to undermine your second strike deterrent? no? then you can see Kahn's argument clearly. don't try to argue that you can still knock-out Russian ICBMs in their silos or SLBMs in their subs by a counterforce strike if need be. you can't, because along with evacuating or taking to good city subway or basement shelters, they also protect their missiles by switching to launch-on-satellite-warning, so that by the time your missiles arrive after a flight time of 15-30 minutes, the silos are empty and the joy of knowing you may have blown up empty Russian silos is cancelled out by receiving their contents! face it: strategic deterrence is only promoted by the Russians because it is a farce that puts the West in a very weak position. Russia has 2000+ tactical nuclear weapons not subject to arms control crap for a very good reason; they have some credibility. We can't even use our most of our ICBM's or SLBM's on dial-a-yield as improvised tactical nuclear weapons against mobile SS25's because most can simply drive out of the 4psi peak overpressure overturning blast circle of American warheads while the latter are in flight, since none of the latter are target-tracking MARV's, but merely fixed coordinate capable MIRV's that can't change trajectory to follow a moving target like the SS25, get it? dictorships aren't always totally dumb].
"... the probability of such an attack by us is small, particularly because we have made negligible preparations to ward off, survive and recover ... Consider the bloody suppression of the Hungarian revolution [of 1956] ... Much pressure was applied for the United States to intervene. We didn't. In fact, there are reports we did exactly the opposite, broadcasting to the Poles and the East Germans not to rock the boat since no American aid was on the way. [now, compare then to now! Eisenhower in 1956 refused to help Eastern Europe in 1956 when the USA had an overwhelming nuclear superiority, less than a year since the first Russian megaton yield nuclear test! Today we are helping Ukraine against Russia when the nuclear situation has reversed. Russia now has fewer conventional weapons than us, but now has more nuclear weapons, of higher average yield, with both ICBMs and dedicated tactical weapons on mobile launchers for more flexible response. all thanks to Russian dominated "arms control".]
"It is possible that a situation as potentially dangerous as the Hungarian revolt could arise again. We could get deeply, if involuntarily involved. ... In 1914 and 1939 it was the British who declared war, not the Germans. ... A thermonuclear balance of terror [Mutual Assured Destruction, the pseudo strategic policy fostered on us by pro Russian appeasement so-called "arms controllers and disarmers"] is equivalent to signing a non-aggression treaty ... no matter how provoking the other side may become. Sometimes people do not understand the full implications of this ... It should be clear that we would not restore Europe by our retaliation ... how many American dead would we accept as the cost of our retaliation? ... if the Soviets were to test our resolve by initiating a series of crises, they could probably find out experimentally, without running excessive risks, how much provocation we would take. No matter what our previously declared policy was, our actual policy and the possibilities would then be verified [e.g., last year Russian government representatives probed the possibilities of falsely claiming that Ukraine has nuclear weapons or radiological weapons, an absurd provocation alleged to be false flag or "Maine sinking" trick to "justify" starting a nuclear war]
"... the problem is to convince the Europeans if we wish to prevent appeasement as well as destruction [mate, that's precisely why France and the UK have their own nuclear deterrents; we're not stupid and are aware that historically it took the sinking of the Lusitania and Pearl Harbor to bring America into WWI and WWII, respectively, after the French and the UK had been fighting for years. bits of paper such as the NATO treaty, or for that matter the 30 September 1938 German-British signed peace collaboration war-avoiding pact, are easily ignored under stress. so it's better to ensure that Western deterrence has multiple buttons to make it really, really credible in Russian eyes. ] ... One of the most important and yet the most neglected elements of the retalitory calculation is the effect of the Russian civil-defense measures. The Russians are seldom credited with even modest preparedness in civil defense. ... This is not only ridiculous, it is also symptomatic of the lack of realism and the prevalent tendency towards undesestimating the enemy. ... the Russians might at some point evacuate their city populations ... they fought a war after the Germans had destroyed most of their existing military power ... Moreover, since 1931 they have had a vigorous program to disperse their industry ... the calculation in which one looks at a U.S. first strike in retaliation for Russian provocation is probably more relevant in trying to evaluate the role that the offense and defense play in affecting some important aspects of foreign policy. Under this assumption, if we have even a moderate non-military defense program, its performance is likely to look impressive to the Russians ..."
[this is precisely why Kennedy, in his 25 May 1961 "urgent national needs" speech to a joint session of Congress reversed Eisenhower's mad ban on American fallout shelters in public building basements in cities, and implemented Kahn's plan, despite James Roy Newman's malicious and lying hate rant against Herman Kahn in the March 1961 pseudo Scientific American. Kennedy also authorised testing of the neutron bomb tactical deterrent plan, devised by Kahn's friend and fellow RAND Corp physicist Sam Cohen, employing the low-yield, relatively-clean Dove and Starling devices developed by Livermore for peaceful ends. Kahn in his longer book of 1960, On Thermonuclear War goes even further against high-yield nuclear weapons by analyzing the absurdity of the "Doomsday" bomb: the bottom line is that Hitler actually made such a WMD in the form of 12,000 tons of tabun nerve agent, which proved useless to deter an invasion, because we had more rubber than the enemy for gas masks (defence) and we could retaliate with mustard gas, anthrax, etc. So Hitler never loaded 12,000 tons of tabun into his bombers, V1 cruise missiles (150 miles range) and V2 rockets (200 miles range). Even in WWII, therefore, the myth WMD's were debunked.
If you divide Hitler's 1945 stockpile of 12,000 tons of nerve agent tabun into the lethal dose of tabun per person (less than 1 mg, i.e. 10-9 ton), you see that according to the kind of statistical nonsense "overkill theory" used with a trembling voice in TV and newspaper "arms controller" articles to get funds, Hitler in 1945 possessed enough tabun to kill 12,000/(10-9) ~ 1013 people, which is obviously cause "arms controllers" to faint, because if true it's a thousand times more than entire world's population! So the loons can claim: "Hitler could have theoretically over-killed the entire world's population by a thousand times in 1945 using his 12 kt of tabun!" But it proved historically as useless to deter our invasion of Germany as our strategic nuclear weapons were to deter Russia's invasion of Ukraine, because of retaliation risks, defences, and exaggerations (unless you use gas in a the Nazi preferred technique of the sealed gas chamber; a fact the Nazis knew all too well from their use of non-persistent Zyklon B aka hydrogen cyanide). Kahn discovered you need a credible deterrent and setting off the Doomsday bomb (whether nerve agent, cobalt or gigaton H-bomb), is just not credible to defend your borders. Nobody can make a credible deterrent out of an incredible action. BTW: These latter words ain't mine: they're a quotation from McNamara in his 1989 UK Channel 4 documentary titled, "The nuclear age: the education of Robert McNamara", where he summarises his (Vietnam war bombing failure to win) experiences, while only getting it half right: he correctly concludes that strategic nuclear deterrence is a load of incredible crap, but foolishly tries to then claim that going back to 1930s disarmament and Russian appeasement is a sure fire way to avoid another world war.]"
ABOVE: 11 May 2023 Russian State TV Channel 1 nuclear testing and nuclear bombing of UK - threats and abuse. Since 2006 we've been dedicated to debunking anti-nuclear propaganda and promoting for how to deal with this situation safely and without war escalating appeasement, using PROVED techniques from the 1st Cold War which are opposed by Putin loving "arms controlling disarmers" who lie about nuclear weapons to try to brainwash the public just as gas war was used in the same way by similar folk to win "peace" prizes in the 1930s to help the Nazis commit genocide and world war. We need YOUR help by reblogging this post please!!! See:
ABOVE: an update on results from getting the message out there as a result of 17 years of this blog. As of Saturday 13 May 2023, blogger statistics show over 2.2 million visits (no idea whether this is from 2006 or 2010; the blog began in 2006 but blogger do not give graphs of statistics going back to whe it began!), to this site, the "peaks" in the statistics occur in part it seems due to the reblogging of blog posts at places like Military Story and The Next Big Future. As stated in the previous post, the history of this blog began in World War Two when dad and his sister were evacuated as kids from Essex which was receiving bombing, to Devon. He contracted TB from contaminated milk as a child which left him emasculated, so was rejected for National Service, but went into the Civil Defence Corps instead, finding recruitment a disaster due to Russian lying propaganda that the UK government wouldn't debunk with its nuclear test data of shelters at Monte Bello. I was encouraged to go into physics by dad to try to do something, but most people in the media aren't interested in reality, just fashionable boring bigotry, celebrity, sophistry, lying and encouraging Russian aggression. Thomas Schelling in the 60s came up with the theory of reversing the principles of war to win a Nobel prize for losing Vietnam, like liars Angell and Philip Noel-Baker who got Nobel prizes for starting WWII.
This "war game" subterfuge of "peace propaganda for universal love via Hitler the man of peace" is like this: claim, like Angell and Noel-Baker, that jaw-jaw is better than war, that all wars are nuclear accidents not the result of jaw-jaw, and you get a prize if you have sufficient celebrity status or academic prestige to use to command media attention, out-lying the other utopian idealists to climb the greasy pole of Nazi-supporting assholes, or you claim that by arms control parity and a surrender of tactical nukes to prevent credible deterrence of Russia, plus refusing to escalate a war rapidly enough to demoralize the opponent into genuine surrender (hardly what happened in Vietnam 1975 or Afghanistan 2021 after "peace talks") - Thomas Schelling's epiphany for peace through negotiating with terrorists (plagarized from 30s Chamberlain, Angell, Joad, Noel-Baker, et al.) - then you are hailed a "wizard of armaggeddon" (Kaplan's term). Wow. You get a Nobel peace prize or better still, like Schelling, the Nobel economics prize for bankrupting your country! All you need to do is you get enough left wing thugs behind you by promising them peace on earth. (You used to also get the Lenin Peace Prize, like Minus Pauling, but maybe that's a bit outdated and stinks of shit too much, don't you know? Oh, and by the way, if anyone wants to bring up religious "be a Christian peacemaker" arguments regarding fighting evil dictators: Jesus's message wasn't to marry Hitler for peace or even to live on your knees under Roman/Russian Dictatorship, but to
"Think not that I am come to send peace on earth: I came not to send peace, but a sword." - Matt 10v34.)
Attempts to show that some arguments, namely those in which both sides are honest and act in good faith, can be resolved by negotiation, so "by logical extension" this proves negotiating with Hitler would have prevented a world war, are fake! Maybe the Nobel Peace Prize can be awarded for Mr Putin and Mr Zelensky to sign a compromise peace deal, maybe a "power sharing" deal like the Northern Ireland sort, where Crimea and Eastern Ukraine are shared between Kyiv and Moscow (and all the dead due to Mr Putin's illegal invasion are quietly ignored to reduce tensions as the two parties pop the Champaigne cork and celebrate)? Even if that "compromise" (note the quote marks) is somehow achieved, a lot of innocent people will have been murdered needlessly due to the "disarmers" of both Ukrainian nuclear weapons and Western dedicated Cohen neutron bombs, deliberately causing the failure to credibly deter the invasion and war from breaking out, and we've been saying this long before Putin invaded. It's not "hindsight"!
ABOVE: the Russian instrumentation and target array methodology on their first nuclear test (RDS1, 22 kt on a 37.5 m high tower, 29 August 1949; high quality declassified 1949 test photos are taken from the 2018 Sarov Nuclear Weapons Museum brochure, linked here) was far more extensive than any Western nuclear test ever conducted, and animals were successfully used to determine the protective factors of shelters and trenches against the combined blast and radiation environment, proof testing almost the entire Russian nuclear civil defense system (it continued to do this at later tests up to and including the 1.6 megaton air burst of 22 November 1955; see the data summary in the DTRA commissioned report Animal Effects from Soviet Atmospheric Nuclear Tests by the Russians V. A. Logachev and V. A. Mikhalikhina of the VNIIEF, Sarov - the protective factor of any shelter or structure is simply obtained from the ratio of the percentage of animals surviving in a structure, compared to unprotected controls - which are unfortunately lumped together for different tests with varying yields and distance ranges to avoid secrecy here). The cost of setting up the 1949 nuclear test site with its 14 target array sectors around ground zero out to 10 km radius was 185,000,000 rubles, including a 560 km cable network which was damaged by the unexpected EMP effect. Key American nuclear test effects data on simple trench and earth covered emergency shelters is still classified secret, since it comes within the bureaucratic province of military structures. America's secret EM-1, Capabilities of Nuclear Weapons, Chapter 15, Damage to Structures, revised in April 1993, Tables 15.17 and 15.18 in Northrop's unclassified 1996 compressed book summary, states that such 6x8 ft military command post and hardened-frame/fabric personnel shelters with 4 feet of earth cover, all require 30, 50 and 60 psi peak overpressure for 50% probability of light, moderate and severe damage, respectively. Northrop's unclassified Table 14.1, Combat Ineffectiveness for Personnel in an Open Two-Man Foxhole (2 x 6 x 4.5 ft) side-on the blast wave shows 50% combat ineffectiveness at 37 psi peak overpressure for a 0.01 kt and 29 psi for yields of 0.1 kt to 1 Mt (so the clean or enhanced neutron bomb is needed for credible deterrence, not just the low-yield option on high yield dial-a-yield weapons that produce trivial neutron doses). These American nuclear test data derived statistics are similar to T. K. Jones' figures - discussed later in detail in this blog post - for the excellent nuclear war survival of Russian expedient blast/fallout shelters. Figure 15.62, Basic vulnerability chart for tunnels in rock, however, shows that tunnel shelters in granite/hard rock, with a highly deformable composite lining between the rock and the tunnel lining (bags full of aluminium metal chips, for instance, were used by T. K. Jones to shock-protect sensitive equipment in successful tests, e.g. a motorbike driven away after surviving a peak blast overpressure of 600 psi, which would be in the crater for a surface burst and well over the peak at ground zero from the air bursts that optimised low pressure area damage to wooden houses at Hiroshima and Nagsaki) survive at just 650 feet or 200 metres from 1 megaton yield.
ABOVE: Left wing Observer aka Sunday Guardian promoting nuclear shelters on 4 July 1982. But are such shelters necessary? New research shown in this post proves that if people can simply descend to the lower floors in the attack warning period (behind tables to shelter from window glass) or to the basements or underground car parks of modern buildings which survive radiation and blast effects far better than the wooden homes in Hiroshima in 1945 (see diagram below from EM1)), the mutual shielding from the "concrete and steel jungle" in a modern city will screen out the radiation and will reduce blast wind and debris hazards. Russia has such basement shelters and tunnel shelters already in cities, as well as evacuation plans and nuclear tested expedient blast and fallout shelters for dispersing the people in a crisis. The American born Lord Chancellor of England, lawyer Lord Lyndhurst (John Singleton Copley, born in Boston, Massachusetts, in 1772) said in his House of Lords Speech, Russia and the Crimean War on 19 June 1854:
"The whole series of her history, from the earliest period to the present day, has been one of long-continued fraud and perfidy, of stealthy encroachment, or open and unblushing violence - a course, characteristic of a barbarous race, and whether at St Petersburg or Tobolsk, marking its Asiatic origin. To go back to the reign of the Empress Catherine, we find her policy in one striking particular corresponding with that of the present Emperor, which policy can be traced back to the Czar Peter. She ostentatiously proclaimed herself the Protector of the Greek Church in Poland, formented religious dissentions among the people, and under pretense of putting an end to disorders which she herself had created, sent a large military force into the country ... With a like policy in the Crimea, the independence of which country had been settled by treaty, she set up a prince whom she afterwards deposed, and, amidst the confusion thus created, entered the country with an army under one of the most brutal and sanguinary of her commanders, and, having slaughtered all who opposed her, annexed this important district permanently to the Russian Empire. ... I pass over the extensive conspiracy in which Russia was engaged with Persia [IRAN] ... against this country ... These scandalous transactions were strenuously denied by Count Nesselrode to our minister at St Petersburg, but were afterwards conclusively established by Sir Alexander Burnes and by our consul at Candahar. ...we ought not to make peace until we have destroyed the Russian fleet in the Black Sea and razed the fortifications ... That she will not remain stationary we may confidently predict. Ambition, like other passions, grows by what it feeds upon. Prince Lieven, in the despatch to Count Nesselrode, to which I before alluded, says: 'Europe contemplates with awe this colossus, whose gigantic armies wait only the signal to pour like a torrent upon her kingdoms and states'. If this semi-barbarous people, with a government of the same character, disguised under the thin cover of a showy but spurious refinement ... despotism the most coarse and degrading that every afflicted mankind - if this power with such attributes should establish itself in the heart of Europe (which may Heaven in its mercy avert!) it would be the heaviest and most fatal calamity that could fall on the civilized world." (For complete validation of this claim a century later, see WWIII nuclear war threat of Khrushchev, made even before Russia had a nuclear superiority, in 1959 - linked below - and Eisenhower's autistic mimickery of Chamberlain's autistic appeasement of Hitler for "peace" on 30 sept '38! The situation is far worse now because there really is a missiles, tactical nuclear weapons, nuclear warhead designs "implementation gap" today in which we are behind, which makes Russian threats credible, unlike 1959!)
ABOVE: 10,000 marched to shout "STOP HITLER" while Chamberlain surrendered Sudetenland for a worthless peace deal. Neither the shouting, nor the "peace deal", nor belated token rearmament, deterred WW2. In the cold war, strategic nuclear deterrence failed time and again: Stalin took over Eastern Europe while Truman had a nuclear monopoly. Only credible tactical nuclear weapons had any effect, judging from protests the Moscow World Peace Council organized across the world against the W79 neutron bomb (see 1977 Secret CIA report on neutron bomb propaganda, below and John Barron's "KGB's Magical War for Peace" book extracts in Reader's Digest below, or see Chapman Pincher's book documenting how Moscow's World Peace Council infiltrated anti-nuclear propaganda via stupid appeasing Western media, "The Secret Offensive") - you need credible nuclear deterrence to force madmen not just listen but to respond usefully. ABOVE: Northrop's Effects Manual 1 (EM1), Tables 15.17 and 15.18 show that simple earth covered expedient shelters have a 50% probability of collapsing at 60 psi peak overpressure, which occurs at just 0.8 mile from a 1 megaton surface burst, but Figure 15.52 (linked here) shows that a simple reinforced concrete tube use as a shelter (concrete stress strength = 4500 psi, with a thickness equal to 10% of the inner radius of the tube) buried under 6 feet of dry or wet soil (note that the curves for wet soil in Figure 15.55 are similar for severe damage at 1 megaton to dry soil in Figure 15.52) has a 50% probability of collapse at 0.3 mile from a 1 megaton surface burst. (The eight deep personnel shelters under London at are much greater depths than 6 feet.) According to Table 6.12 in the 1957 edition of Glasstone's Effects of Nuclear Weapons, Britain's 1939-designed World War Two standard issue corrugated steel arch outdoor Anderson shelters if enlarged to 20-25 feet span (which increases vulnerability, since smaller arches have a smaller exposed area and so receive lower blast loading) and using 10 gage steel with 3 feet earth cover (over the crown), will half collapse (i.e. collapse the side facing ground zero) at 30-35 psi peak overpressure, and will completely collapse at 35-40 psi peak overpressure, based on the 1955 Teapot nuclear test series in Nevada. However, following careful nuclear tests on such shelters during the 1957 Plumbbob series in the Nevada and the 1958 Hardtack series in the Pacific, the "earth arching" protective effect of soil cover was discovered and better understood, so that Glasstone's revised 1962 edition of Effects of Nuclear Weapons stated in Table 4.45 (which is reprinted unaltered as Table 5.160 in the 1977 final edition of Effects of Nuclear Weapons) that such shelters with 5 ft earth cover require 45-60 psi peak overpressure for collapse. This revised table also shows that a reinforced concrete arch 8 inches thick with a span of 16 feet and 4 feet of earth cover will require 220-280 psi peak overpressure for collapse. The earth arching and earth shielding effect is the simple, nuclear bomb-tested survival principle behind Cresson Kearny's 1979 Oak Ridge National Laboratory manual, Nuclear War Survival Skills, and the UK government's 1982 Domestic Nuclear Shelters - Technical Guidance 2nd edition (extracts linked here with additional detailed relevant nuclear test data, see illustrations below for the 1982 version of the earth covered 1939 WW2 Anderson shelter - based on data from American and British nuclear tests, from the 1952 Monte Bello Operation Hurricane shot onwards). ABOVE: the report on the radiation shielding by simple, quick, and cheap US Civil War, WWI and WWII-style trench shelters exposed at the UK Hurricane nuclear test in 1952 was classified Secret, although it states in paragraph 13.1.1: "The experiments described in this section show that slit trenches provide a considerable measure of protection from the gamma flash. From the point of view of Service and Civil Defence authorities this is one of the most important results of the trial." This cover-up even after the data is declassified ensures that in a nuclear attack, many people kill be needlessly killed. Thugs believe this will help disarmament propaganda or other propaganda rubbish that totally failed when tried out prior to WWII. Despite this hard-won data being recognised for its importance for civil defence, this data was never published in any UK civil defence manual, handbook or advertisement, and is still covered up, like the rest of the taxpayer funded nuclear test research. When you combine such simple shelters for essential key workers in target areas with crisis evacuation (or "relocation" if "evacuation" is too invocative of September 1939) for the remainder of a city, you achieve a credible war survival strategy that undermines strategic nuclear deterrence. (An enemy can still bomb an evacuated, sheltered city to cause building damage and contamination, but historically this just backfires, increasing the morale and determination of the opponent to fight back.) America for long used secret data from the 1945 combat attacks on Hiroshima and Nagasaki as its primary data source, classifying the detailed 6-volume Strategic Bombing Survey reports from nuclear use in Japan Secret, and never publishing them or releasing them on the internet (it did not want Russia to have the information), and it did not need to expose a house to a nuclear blast wave until 1951 at Operation Greenhouse. This backfired due to the direct information Russia obtained from its own nuclear tests. (Similarly, Britain obtained independent data debunking American anti-civil defence propaganda lies on survival in flattened houses, which it used to the horror of Russian biased arms control and disarmament folk; the CND style liars simply claimed falsely that faked style American "data" somehow was more reliable than proof tested British data, whose origin was classified secret due to the Marxist infiltrated British bureaucacy which behaved basically as more subtle, even more effective Russian military propaganda front than the better known Cambridge Spy Ring; this thuggery on nuclear weapons capabilities in the UK media continues to this day via Corbyn et al., who are "respected" on nuclear lies by all UK leading "civil defence historians", "cold war historians" and related propagandarists who know nothing about the nuclear effects secrecy problem.) Recent official publications by the designers themselves of the latest Russian thermonuclear warhead designs, shows equally high quality research, contrary to popular misconceptions. ABOVE: Secret nuclear weapons stockpile history showing that in May 1949 (the month the Berlin Blockade ended), that the USAF knew using Hiroshima and Nagasaki capabilities of nuclear weapons data that 133 nuclear weapons USED STRATEGICALLY would not win a war against a nuclear unarmed opponent! Hence the increase in American interest in TACTICAL nuclear weapons. Teller wanted the H-bomb because he knew toss all about the effects of nuclear weapons, and didn't want to know the facts, as proved by Dr Frank H. Shelton in Reflections of a nuclear weaponeer which first exposed the crater size lies in Glasstone's book. Teller lies about the firestorm in Hiroshima in his 1962 Legacy of Hiroshima book, which says the exact opposite to the secret 3 volume US Strategic Bombing Survey report (volume 2 of which is specifically about the firestorm, which was set off not by thermal radiation but by blast overturning thousands of charcoal braziers being used to cook breakfast, and the breakfast-timing was also the reason why no air raid alarm was sent out, according to Yoshi Oka, the Hiroshima air raid sirens operator who survived near ground zero). ABOVE: Polish Harvard Professor Richard Pipes, who had no love for either the Nazis or the pseudo-Communist nuclear thugs who seized his homeland, famously debunked the bigoted pseudo-pacifists in charge of promoting the 1930s style US Arms Control and Disarmament Agency appeasement/peace deal lies about nuclear war annihilation in his July 1977 Commentary paper, without getting into classified data on nuclear warhead designs or Russian nuclear tests on house and shelter survivability: "When he was age 16, Pipes laid eyes upon Adolf Hitler at Marszałkowska Street in Warsaw when Hitler made a victory tour after the Invasion of Poland. The Pipes family fled occupied Poland in October 1939 and arrived in the United States in July 1940, after seven months passing through Italy. Pipes became a naturalized citizen of the United States in 1943 while serving in the United States Army Air Corps. He was educated at Muskingum College, Cornell University, and Harvard University." ABOVE: in 2009, the Russians declassified and published a book containing some original reports on the design and testing of two-stage nuclear weapons from 1954-1956, including 1956 designs for 150 and 1000 megaton bombs using either natural lithium deuteride (7.42% lithium-6 abundance) or enriched lithium-6 deuteride (the enriched 150 megaton bomb has 100 tons i.e. 1.5 Mt/ton yield to mass ratio, but the unenriched one has 500 tons mass, i.e. 0.3 Mt/ton ratio). However, for that year they ordered production of just ten 1.8 megaton yield bombs and another ten 0.5 megaton bombs. They also ordered a 20-30 megaton bomb with a yield of 20-26 tons (i.e. a yield-to-mass ratio of around 1 Mt/ton) for air burst testing. The 14 January 1954 original design paper by Sakharov and Zeldovich attributes the two-stage idea to Davidenko, but it proposes using a boron filling to convert all of the x-rays from the fission primary into a shock wave to compress the fusion stage. Later, on 9 December 1954, another paper by Sakharov and Frank-Kamenetsky works out the details of a specific design: a 15 ton bomb yielding 7.5 megatons which produces a 10 fold compression of the density of the low density fusion fuel inside a spherical, dense (uranium) pusher-tamper. This was a pathetic 0.5 megaton/ton yield-to-mass ratio. It was only through the efforts of Yuri Trutnev (see quotations from him, later below in this blog posting) that the efficiency of the design was massively improved, firstly by changing the boron case filling into a spherical layer surrounding the fusion fuel to absorb case-channelled x-rays and convert them into an inward shock wave to compress the fusion fuel only (not a shock wave from a general case filling that will act in all directions, and blast the bomb apart rapidly). In their Livermore paper UCRL-74116 (PDF linked here on the IAEA server and here on the US Government's OSTI server), Nuckolls, Wood, Thiessen, and Zimmerman explain: "... the optimum pulse shape is determined by considerations of entropy and Fermi-degeneracy,
hydrodynamics and Raylelgh-Taylor instability, and thermonuclear ignition and self-heating. The required implosion symmetry is achieved by irradiating ... from all sides ... as well as by electron transport in the atmosphere ablated from the pellet. Taylor
instability is suppressed by sufficiently rapid imploclon as well as by generating the implosion pressure by subsonic ablation driven by diffusive electron transport. ... These hot electrons transport throughout the atmosphere heating electrons (via electron-electron collisions) to temperatures which increase from one to 10 Kev. The pellet surface is heated and ablated by the hot atmosphere, generating pressures which optimally increase from 106 to 1011 atmospheres." This paper adds that "hundreds of implosion/burn computer calculations" were used to identify the optimal Lagrangian implosion pressure-time history equation, and then that equation was used to identify the optimum input x-ray energy pulse shape needed to achieve the optimal Lagrangian for the most efficient thermonuclear fusion. The rate of supply of X-rays from the fission primary stage (or laser in clean burns) is then controlled by the design of the latter and by plastic foam baffles which deliver the X-rays to the fusion capsule. (There is a discussion in Livermore's UCRL-LR-105821-97-1 (pp. 22 et seq.) of low density foam shells such as aerogels for fusion capsules.) Another Livermore report, UCRL-80164, on Exploding Pusher Performance by Rosen and Nuckolls explains that denser pushers work by exploding, with half the mass of the pusher explosing outwards and the remainder imploding inwards and compressing the capsule: "The imploding half of the shell acts as a piston, driving a shock through the DT that principally heats the ions. ... Whereas the high-compression, isentropic implosion targets are sensitive to electron preheat and to Rayleigh-Taylor instability, exploding pushers, by virtue of their rapid thermal wave early heating and by their non-ablative implosion dynamics, are not sensitive to the aforementioned problems." (This paper cites Nuckolls' Secret-Restricted Data UCRL-50000 71-5, 1971, as reference 1.) On the subject of x-rays and plastic foam: Glasstone and Dolan's 1977 Effects of Nuclear Weapons, paragraph 7.79 on pages 307-8 states that for a typical nuclear explosion reaching 10,000,000 K temperature, i.e. very soft 4.3 keV predominant x-ray energy (considerably lower energy than medical x-rays which are often well over 50 keV), the mean free path in sea level air is only 15 cm, so that 90% are absorbed within 1 foot of sea level air. Clearly, therefore, sea level air will stop these x-rays from ablating surfaces of a secondary stage more than a foot or two from the primary stage. Howard Morland, Richard Rhodes and Chuck Hansen don't mention this problem for the 1952 Mike design. Was there a vacuum pump to clear the "radiation channel" of the sea-level air that will stop or seriously attenuate virtually all the x-rays? Or is the presence of air in the radiation channel used to diffuse the x-rays in all directions to a uniform concentration, allowing isotropic (similar from all directions) ablation of the secondary? Howard Morland, Richard Rhodes, and a British AWE Aldermaston paper in Nature on the "Science of Nuclear Warheads" (linked and quoted later, below) all refer to polystyrene in nuclear weapons, a plastic with approximately the density of water, i.e. over 700 times denser than air, thus cutting the mean free path of 4.3 keV x-rays to just 0.2mm! So any significant thickness (over 1mm for example) of polystyrene will completely absorb the soft x-rays from a primary stage heating the surface of the polystyrene, although re-radiation can occur from the heated surface, which behaves like a diffuse or Lambertian reflector, i.e. Teller's "radiation mirror" in the title of his and Ulam's famouse 1951 report, On Heterocatalytic Detonations I: Hydrodynamic Lenses and Radiation Mirrors. If you fill the entire radiation case with polystyrene, however, you get a partition of energy between the kinetic energy of the colliding carbon and hydrogen ions and electrons (plasma) from the heated polystyrene, and x-ray energy which is being produced and absorbed by that ionized plasma. The percentage distribution of energy partitioned between matter and x-ray radiation is a sensitive function of the temperature; the energy in matter being directly proportional to the temperature, while the energy in x-rays is proportional to the fourth-power of temperature (see for instance: H. L. Brode, Annual Review of Nuclear Science, v18, 1968, pages 153-202). For "cold" 1 keV x-rays (2,300,000 K) a large percentage of the energy is in the material plasma, but for "hot" 10 keV x-rays (23,000,000 K), most of the energy is in x-rays even within the plasma. The exact x-ray temperature emerging from the primary stage is a function of the shielding of that stage by hydrocarbon plasma from the chemical implosive system used to compress the primary stage core, and the beryllium neutron reflector. If the primary stage is a 2-point implosion elongated or egg shape, much hotter (higher energy) x-rays will emerge from the smaller-diameter sides which have less shielding than the long axis. For very low energy x-rays from older spherical primary stages, lower density foams (Seabreeze and Fogbank have very low densities, closer that of air than polystyrene) are used to keep more of the case filled energy in x-ray energy than in the material plasma (ions and electrons), than is the case for polystyrene. Any such material filling the radiation channel will slow the transit of x-ray energy by diffusing it, which allows more time for neutrons from the primary to arrive and begin to fission (predetonate) any fissile material present in the secondary stage (this is not the case for a clean secondary stage, where those neutrons are actually needed to fission lithium to yield tritium, prior to implosion). Since force is the rate of change of momentum, F = dp/dt, it is undesirable to fill the radiation channel with anything, if you want to maximise the x-ray ablative recoil force on the secondary stage! But do you really want to maximise that impulsive force? Is maximum impulsive force the best way to achieve the greatest amount of secondary stage compression? It turns out, it simply isn't. This was discovered by Nuckolls in the late 1950s and proved in the very clean Ripple nuclear tests during Dominic in 1962. The maximum impulsive compression is given by using a vacuum radiation channel and using the approximately 10 ns width pulse of x-rays from the primary stage to ablate a dense metal pusher on the surface of the secondary stage. But against this factor, you must consider: (1) the problem of how to diffuse those x-rays uniformly all around the secondary stage (easy with a foam filling, even for a spherical shaped secondary stage), and (2) the problem that maximising the ablative force as an abrupt, impulsive shock wave through a dense pusher increases entropy, heating the pusher, whereas a gentler, more nearly isentropic rate of delivery of energy keeps more of the applied energy in the compression of the secondary stage, rather than in heating the pusher. It actually makes no sense, Nuckolls discovered in 1961, to waste any of the limited amount of energy from the primary stage on heating up the secondary stage's pusher by using inefficient, entropy increasing shock compression. There is confusion possible here over Theodore Taylor's levitated primary stage analogy of swinging a hammer to hit a nail, rather than placing the hammer on the nail and pushing it gently. But this is an illusion caused by the threshold force needed to push a nail into wood: you would not use a hammer blow to push a tin-tack into a cork notice board to hold the corner of a poster to the wall! The hammer is needed for the nail in order to integrate muscle power for a second or so, into kinetic energy of the hammer. You don't have enough power in your arm to drive the nail in by simply pushing the nail into the wood. By analogy, the kilograms of chemical explosive in the primary stage lack the power to directly compress the metal shell to a maximum density, just as your arm can't directly (without the power-integrating mechanism of the swing of the hammer) push a nail into hard wood. In the primary stage, chemical explosives are assisted by having pit levitation, so that the chemical implosion can deliver power into the pusher for a period of time, to give it as much kinetic energy as possible before it hits the hard-to-compress core. Otherwise, the mismatch of acoustic impediance of the low density (carbon and hydrogen ion) explosion debris pushing at the metal pit causes the pit to reflect the energy back, rather than absorb it and be compressed. This is simply conservation of momentum: throw a thousand footballs at a wall with low energy, one after another, the footballs will bounce off, with minimal energy delivery to the wall and thus minimal compression or net motion of the wall. It's almost an elastic collision; the low density footballs bounce off the wall with almost the same kinetic energy as they struck it! But if you deliver the same energy as a single iron cannon ball, collision is less elastic and more energy is coupled into the wall! This is more useful for pushing the wall. This is not secret or highly sophisticated mathematical physics, but simply the kind of common sense we all have from experience in the real world. So with the larger amount of x-ray energy from the primary stage, the situation is not like trying to push a nail into hard wood (as for the smaller energy from 20 kg of TNT to compress a metal shell) or to knock a wall down using footballs, but is more like the tin-tack being pushed into cork. Provided that your x-ray ablator (say beryllium) is of relatively similar density to the lithium deuteride fusion fuel you are trying to compress, there is little acoustic mismatch and energy is then coupled efficiently rather than reflected. So you are in the situation of being able to push a tin-tack into cork, rather than having to swing a hammer blow on a nail. If there is a dense fissile "spark plug" in the centre of the fusion stage, it can be levitated to ensure it is delivered a hammer blow by a dense pusher shell. ABOVE: Secret 1956 USSR order to equip their 8000 km range R-7 ICBM with their 2 megaton warhead with 2900 kg mass (the warhead mass quoted is the important secret, since it is the payload for the missile, and was previously secret), based on their 1.6 megaton 22 November 1955 test at Semipalatinsk. This report states that their previous 400 kt tested yield 1953 hydrogen bomb design (Teller's externally-pit-boosted or single-stage Alarm Clock RDS-6s) would require a mass of 3400 kg to yield 1.5 megatons, so the lighter new two-stage design increased the R-7 missile range by 200-300 km. That was the only megaton range test at Semipalatinsk because further high yield tests there were banned after it destroyed the local meat processing factory. Yuri A. Trutnev (First Deputy Scientific Director of RFNC-VNIIEF) explains how a 500 kt yield limit was imposed on Semipalatinsk after the 1955 test of 1.6 megatons caused damage: "it was recommended to put into service a certain [double-primary] version of the product. And so, one of the products was delivered to the Semipalatinsk test site for testing, a product developed under the guidance of Evgeny Ivanovich Zababakhin. He claimed that the power of the explosion would be on the order of 0.5-0.6 megatons. I note that at that time there was a ban on carrying out explosions with a capacity of more than 0.5, because as a result of an explosion with a capacity of 1.5 megatons, the Semipalatinsk meat processing plant was destroyed. And here we are, no weather, nothing to do, I decided to read the reports. I took Zababakhin's report, I compare the calculations with ours, and I see: yes, there is not 0.5, not 0.9, all 1.5 megatons should work out there! I could be silent, but if 1.5 megatons will again “destroy” the meat processing plant? At one of the meetings, I reported this to the test leader. As Zababakhin fell on me: “This is a disgrace, this is not the case, this is ugly! You specifically say to remove our bomb from the tests. Honest people don't do that!" I suggested: "Let's see together." He did not look at anything, slammed the door and left. And it's good that they didn't try it! Because the next year in the north we blew up our version of the product and received about 0.6-0.8 megatons. On the occasion of our success, they poured me a glass of cognac: “For the victory!” It is noteworthy that it was February 23, 1958, the day of the Red Army. In the same year, 1958, we began to prepare the next session on the basis of the 49th project. There were attempts to delay the tests, and the ministry had no desire to test products of lower power. ... And they tried it, and everything worked out. This development subsequently became the most important basis for improving the thermonuclear arsenal of our country." In addition to moving to double-primary theormonuclear weapon design, they also finally conducted their first ever gaseous tritium and deuterium boosted plutonium pit primary stage test on 28 December 1957, yielding an "amazing" 12 kt (below). ABOVE: how to uniformly compress a secondary fusion stage using x-rays without problems from the reduced x-ray intensity on the side of the secondary which is furthest from the primary stage (due to the "x-ray shadow" created by self-shielding on the secondary's far-side from the fission primary stage, by x-ray shielding due to the presence of the secondary stage itself). This problem has several possible solutions which are discussed in detail later in this post, including quotations from the actual Russian nuclear weapons designers articles and declassified reports. On April 10 and 16, 1957, Russia tested shaped new, improved two-stage thermonuclear designs, yielding 680 and 320 kt, respectively. The final R-7 warhead design, RDS-46A, was proof-tested on October 6, 1957, yielding 2.9 megatons. (Since elongated secondary aka thermonuclear stages become spheres when subjected to linear implosion from two primaries, or two two-stage thermonuclear devices as in the 50 megatons Tsar Bomba and lower yield cleaner devices, and since pear or egg shaped secondary stages become spheres when properly compressed by the anisotropic x-ray exposure from a single primary in devices without foam equalizers filling the case, we will generally depict secondaries as being spheres later in this post; even when they are elongated prior to compression.) It turns out that the first Russian two-stage device tested in late 1955 with 1.6 megatons yield (it was designed to give 1 megaton) had a secondary stage which was a sphere when compressed (it may however have been egg or pear shaped prior to compression, as shown above, in order to allow for the anisotropy of x-ray delivery to a spherically-compressed secondary stage when using a single primary, without the use of a foam filling to disperse x-rays to a uniform energy density throughout the case). The designer testimony (Yuri Trutnev) states that the secondary stage used in 1955 had a low-density ablative material layer (e.g. beryllium metal, or plastic foam) around it (not filling the entire radiation case, unlike Western designs with spherical secondary stages). Yuri Trutnev: "I knew that when they explode, a lot of energy comes out in the form of x-rays. And I began to think about how to make it so that the thermonuclear charge is overlaid with a light substance - "coating", these can be chemical elements with a low number, having very good thermal conductivity, and with the help of X-ray radiation from the explosion of the primary atomic charge "coating" heat up. At the same time, its substance would evaporate outward, towards the radiation, and as a result, as during the movement of a rocket, a reactive impulse would be created, directed into the secondary charge and creating the pressure necessary for effective compression of the thermonuclear "fuel"." (The day after seeing that successful 1955 test, Yuri Trutnev told his colleague Yuri Nikolaevich Babaev another idea, the idea for using two primaries, one on each side of the secondary stage, which was assigned product number 49, weaponised by the deputy director of the lab, and air drop tested on February 23, 1958, becoming the basis for today's cheap thermonuclar warheads made by Russia; all of this will be discussed later in detail in this blog post, since .) This would have caused a far gentler (slower) compression of the secondary stage than when using a dense U238 or lead ablator, thus increasing what Lawrence Livermore National Laboratory weaponeer Nuckolls calls "approximately isentropic" (unchanged entropy) shock compression, which is more efficient since more of the compression energy remains in compressive mechanical work, rather than being turned into heat energy (you want the secondary stage to be as compressed as much as possible without wasting that energy as heat; heat is generated by fission in the compressed oralloy layer or the spark plug core of the secondary stage, or in clean secondary stages, in fusion of D+T gas in the core, following its extreme, isentropic compression, as used by Russia from 1965 for more efficient thermonuclear weapons). ABOVE: the Russian 1955 thermonuclear weapon with a low density ablator is similar to a system described for evaluation purposes in a declassified 2011 Jason report, Hydrodynamic and Nuclear Experiments (JSR-11-340, Secret-Restricted Data before deletions such as the deletion shown above) on pages 72-3 compares the shock compression versus the isentropic compression of beryllium coated plutonium pits in nuclear weapons by different shapes of x-ray energy pulse. It notes on page 21: "The National Ignition Facility [NIF] utilizes laser drive to compress samples using shock or quasi-isentropic compression [Emphasis added], potentially to in excess of 100 Mbar. Currently, samples have been ramp compressed to 50 Mbar. It can also be used to explore high strain rates (up to 107 /s). It has not yet been qualified to handle Pu, but has provided important data on surrogates such as Ta." Shock compression is an abrupt hammer-blow produced by a fast-rising, brief pulse of x-ray energy, whereas the less abruptly rising pulse of isentropic compression is a reversible adiabatic pressure wave such as sound waves, which for high energy densities must be produced by a more gradually ramping, longer pulse of increasing energy density; this increases the proportion of the energy in kinetic energy of particles (dynamic pressure) rather than in internal energy (overpressure and heating). Pure isentropic compression would violate thermodynamic physics, but quasi-isentropic compression is possible. A simple analogy is hitting a door with a hammer blow, versus gently pushing a door closed. Hitting the door wastes some energy in sound waves, oscillations, and heating, causing a large, abrupt and wasteful rise in the entropy of the system, whereas a gentle push maximises the fraction of delivered energy which goes into kinetic energy of motion of the door causing it to pick up momentum efficiently and swing in the desired direction, minimising the energy wasted as sound, oscillations and heating. For a gas, isentropic flow does not imply that temperature is constant, only that entropy is constant: ABOVE:We can get rid of the natural logarithms in this isentropic solution, Cvln (T/T0) = -R ln (V/V0), by raising both sides to become powers of the base, e, thus: T/T0 = (V/V0) exp(-R/Cv) = (V/V0) exp(1 - gamma). Nuckolls et al provide the idealized equation for the x-ray delivery rate of energy required for isentropic compression of the secondary (fusion) stage in nuclear explosives, in a paper openly pubished in Nature, v239, p139, 1972 (extract is linked here): (1 - t)-1.875 where the 1.875 is from 3{gamma}/{gamma + 1} = 15/8, gamma being the ratio of the specific heat capacity at constant pressure to that at constant volume, for dense hydrogen with degenerate electrons (where gamma = 5/3), and t is time measured in units where 1 unit of time is the time taken for the shock wave to reach the centre of the secondary stage. You can't ever achieve this idealized isentropic energy rate, but you can do your best (any movement of the curve from an abrupt shock to a gentler rise increases the isentropic conpression contribution relative to shock compression, so it is not true that you need a "perfect" fit to the idealized isentropic pulse delivery curve, which approaches infinity in the asymptotic end limit anyway!), and Dr John Nuckolls successfully proof tested this "Ripple" concept with multimegaton 99% clean atmospheric nuclear tests during Operation Dominic in 1962, which will be discussed in detail later. The quasi-isentropic compression in the 1955 Russian thermonuclear test with a low-density x-ray ablator rather than the high-density ablators used by America, may account for the fact the yield was 60% greater than predicted (presumably the prediction ignored isentropic compression): 1.6 megatons measured, versus 1.0 megaton prediction. Since the Russians did not use tritium plus deuterium gas in the core of their secondary stage in 1955, the contribution of isentropic compression was probably marginal, but the low-density ablator would have come into its own when Russia placed deuterium plus tritium gas into the core of the fusion charge in their 27 October 1966 test, yielding 700 kt. Russian has always prided itself on over-educating its population in advanced physics (poster below). Our point here is just that the Russians seem to have replicated the TWO key features of the isentropic Ripple design (a low density ablator to replace a dense ablator, and T+D gas in the core of the fusion charge) and compressed these into smaller devices for MIRV warheads (an approach rejected by the USA, despite its rhetorical use to attack Russian competence, by AEC Chairman and plutonium discoverer Glenn T. Seaborg in a tape-recorded secret response to President Kennedy's question of what Russian nuclear warhead designers would make of the secrets of the American thermonuclear warheads; this issue will be discussed further, later in this blog post). Isentropic compression nuclear warhead design details were declassified because of its alleged relevance to "clean nuclear fusion power" pipe dreams. In reality, this is purely clean nuclear weapons research, because to make it efficiently generate electric power you'd need to be setting off huge H-bombs regularly to generate significant heat to justify the expense! The declassified 1955 two-stage Russian thermonuclear case design was called by the Russians "pear-shaped", possibly due to the fact that a pear-shaped secondary stage, when compressed by the anisotropic x-ray environment produced by a single fission primary stage, becomes an ideal sphere with maximum fusion burn efficiency (above) for that single primary design (without a foam x-ray diffusive equalizer, which slows down the x-ray ablative secondary stage coupling mechanism, thus increasing the number of neutrons that arrive in the secondary stage prior to full compression, leading to the need for a neutron shielding interstage to prevent pre-detonation of an oralloy loaded secondary). There is also a relevant 1975 US patent, "Foam encapsulated targets", US4376752, by nuclear weapons designer John H. Nuckolls (who has explained elsewhere, as we will quote below in this post, how such research led to four successful isentropically compressed, very clean megaton tests during 1962, authorised by Kennedy) and two others which states: "... a quantity of thermonuclear fuel is embedded in low density, microcellular foam which serves as an electron conduction channel for symmetrical implosion of the fuel ..."). Nuckolls explains the physics of spherical stage thermonuclear burn efficiency beautifully in his 1973 report UCRL-74345: "The rates of burn, energy deposition by charged reaction products, and electron-ion heating are proportional to the density, and the inertial confinement time is proportional to the radius. ... The burn efficiency is proportional to the product of the burn rate and the inertial confinement time ... Much higher pressures are required if the electrons in the high density DT are not Fermi-degenerate, i.e. if the implosion is not essentially isentropic. The pressures applied to implode the pellet must be uniform spatially and temporally to less than one part in twenty in order to preserve effective spherical symmetry. ... The hydrodynamlc Rayleigh-Taylor Instability must be controlled. Otherwise the pellet surface cannot be relatively gradually accelerated during the implosion as required by the optimum pulse shape." Nuckolls also states on page 15 that most of the energy supplied to the fusion capsule is lost in the ablation process (the hot blow off material has the velocity of sound for the heated surface temperature) so that only a coupling efficiency (i.e. the fraction of supplied x-ray energy that results in implosive compression of the secondary state) of 2-15% is available to compress the fuel; this coupling efficiency is given by the very simple equation: (1/2)v/C, where v ~ 10-300 km/s, is the fusion capsule implosion velocity, and C ~ 200-1000 km/s, is the velocity of sound for the blown-off plasma.
ABOVE: the American problem with discarding the 1962 isentropic breakthrough and instead using an expensive highly-enriched U235 aka "oralloy" ablative "pusher" (external spark plug around the fusion fuel capsule in the secondary stage of classic cylindrical shaped American two-stage devices), to increase the yield-to-mass ratio for compact nuclear weapons like the B61 and its alleged smaller derivative the W80, is the critical mass of the oralloy pusher. You can't put a whole load of U235 concentrated in the bomb's secondary stage to give a huge yield, or it is critical (and you have a nuclear reactor, not a bomb!). One solution to this critical mass issue in secondary stages, particularly for cylindrical secondary stages, is for relatively small rings of oralloy to be separated by larger diameter neutron absorbing "washers" of, say uranium-238 or possibly lithium deuteride (above right; oralloy is colored blue, U238 washers are white), as suggested by the declassified nuclear weapons film, Developing and Producing the B-61 (see 10 minutes, 7 seconds into the video - screenshot below - where the B61's entire secondary stage assembly is seen undergoing "criticality studies of the nuclear assembly", and compared to 12 minutes 21 seconds where the partial assembly components of both pit and secondary stage are displayed). This film also shows an axial rod through the centre of the secondary stage and an x-ray baffle separator in the middle of the secondary stage, which we will ignore for the present. Teller's original "sausage" secondary concept was for a series of secondary stages connected like sausages, x-ray irradiated and imploded one at a time, with baffles separating them, because if there was just one very long cylinder, the axial fissile spark in will be initially compressed properly only near the primary, and then will pre-detonate itself along the remainder of the spark plug before the remainder of the secondary has been compressed (the x-rays may go a light velocity in a vacuum, but the compression of the secondary, whether by shock or isentropic, is much slower!). Details of the axial central rod through the B61 secondary stage are shown below, in stills from the same declassified film.
The alternating rings along the secondary stage in this design makes the surface area of the secondary stage rippled, a concept that increases its surface area for absorption of x-rays, which was the original motivation for Teller's ambitious but failed 1954 Morgenstein (spiked secondary stage Operation Castle shot 3) nuclear test at Bikini Atoll. Even excluding the issue with computing and achieving the geometry of isotropic compression of a sphere by radiation from a single primary, Teller at first did not want the spherical secondary stage (used by Russia in 1955) in American nuclear weapons, because the soft 1-10 keV x-rays that couple energy between stages are absorbed in a very thin surface layer of the secondary, so the surface area of the secondary stage is crucial, and is minimised (not maximised) for a spherical shape. This means that, because a sphere mathematically has the MINIMUM surface area to volume ratio of any shape, a sphere absorbs the MINIMUM possible fraction of the x-rays from the primary stage. So the sphere is the WORST design possible, if you want to maximise the coupling of x-rays to the secondary stage. This is not speculative or a matter of secret computer designs of classified weaponry: it is very simple mathematically for a kid to prove that far more x-ray energy will be absorbed by the inside of the weapon casing than on the outer surface of a spherical secondary stage. Teller's Livermore laboratory, however, even in 1954 at the Morgenstein test of Castle, tried to get around this problem of the small surface area absorption of soft x-rays by the surface of a sphere, by hugely increasing the surface area of the "sphere" by making its surface "spiked" or convoluted so it will absorb a larger fraction of the x-ray energy from the primary stage. This may also improve the stability of axial compression in a cylindrical secondary stage, where (unlike early designs like Mike in 1952) a very small primary (5 kt unboosted or 10 kt boosted) is used to axially compress just a very small part of the secondary stage near the primary stage in an x-ray radiation channel confined by a seabreeze x-ray baffle foam.
In the Mike "sausage" and other earlier Castle nuclear designs, x-ray baffling foam was not used in this way to fill most of the case and create a radiation channel confining the initial fusion burn region, but was just used as Teller's "x-ray mirror" (a layer of plastic hammered on the the lead lining of the steel case with nails, to reflect some x-ray energy back on the secondary stage, and to prevent high-Z lead ablation debris quickly filling the radiation channel and killing the coupling). So it appears the Mike "sausage" design required a larger yield primary stage to compress the entire clyinder, whereas the use of x-ray attenuating foam to limit initial exposure of the secondary stage to a few rings near the primary, reduces the size of the required primary. Once the fusion burn begins in a limited part of the secondary, it releases x-rays which then help to compress and ignite fusion in the remainder (this is the brains of the American secondary design, requiring very sophisticated computer modelling as well as back-up nuclear testing to verify them). A declassified film of the B61 shows the secondary stage of the B61 (and presumably its scaled down version, the W80) being tested, a rippled cylinder with rounded shielding end caps (below). This appears to be an entirely different concept to Russian nuclear warhead design.
Another option, which the Russians first tested very successfully in 1958, is to simply put two smaller fission primary stages into a radiation case, one on each opposite side of the fusion capsule, as shown below, with the two sets of neutron initiator tubes and detonators, corrected in parallel circuits - there is a delay between conventional explosives and neutron guns firing to allow for the time it takes to compress the fissile cores - via high-current, fast vacuum tube switches called krytrons. However, Britain and America (for reasons discussed later, below) completely ignored this possibility, and the American Los Alamos nuclear weapons designer of devices Scorpion, Hamlet, Viper, Davy Crockett and King, Dr Theodore Taylor, dismissed the key Russian double-primary thermonuclear warhead design when presented with it by author John McPhee: "'The shape tells you a lot about H-bomb design,' Taylor said again. 'But not enough.' I drew a sketch of a hydrogen bomb showing a cylinder full of thermonuclear fuel, with two fission bombs, one at each end ... he said, 'Nice try, but that is not what happens'." (This quote from J. McPhee, The Curve of Binding Energy, Farrar, Straus and Giroux, NY, 1974, p149. This dismissive error was then repeated again in response to Chuck Hansen's 27 August 1979 letter to Senator Charles Percy of Illinois, which contained the diagram shown below, which Howard Morland dismisses incorrectly in his book, The secret that Exploded. This casual dismissal of double primary designs may well mean American efforts to deduce Russian nuclear weapon design from fallout samples by analogy to the designs America tested in the past, were plain wrong. Certainly, Russia tested two-stage, single-primary weapons; but their most compact efficient designs are provably double-primary for 0.1-1 megaton yields and use two thermonuclear stages for both cleaner and 1-100 megaton-yield fusion tertiary stages.)
On 23 February 1958, Russia tested the new, radical Babaev-Trutnev compact design of thermonuclear weapon (above; detailed documentary evidence from multiple sources is provided later in this post), a pipe containing a spherical fusion stage sandwiched between two fission (primary) implosion charges, wired in parallel circuit for simultaneous firing via a krytron high speed, high current vacuum tube switch. This was a relatively small diameter 860 kiloton deliverable thermonuclear weapon, weaponised by Vladimir Fyodorovich Grechishnikov (Deputy Chief Designer of VNIITF, Snezhinsk) and detonated at 2500m altitude (the long range American detectors, which were less accurate than close-in Russian instrumentation, suggested that this Russian test 52, codenamed "Joe 46" by America, had a yield of 1.2 megatons and a burst height of 3200m). Litvinov gives details of the development of this bomb into modern Russian nuclear weapons in his report to the 3rd Historical Conference on the History of the Nuclear Weapons Complex of Russia, Snezhinsk, June 16-19, 1998, Development of Nuclear Charges at the RFNC-VNIIFT (1963-1976) (first published on pages 135-145 of his book, Nuclear energy is not only for military application, published by the Ural Branch of the Russian Academy of Sciences, Ekaterinburg, 2002, and now available online on pages 536-547 of his Selected Works, published by VNIITF, Snezhinsk in 2014, linked here:http://elib.biblioatom.ru/text/litvinov_izbrannye-trudy_2014/go,0/, whose page numbering we will quote from in the list of key Russian nuclear weapons design developments, below). Litvinov there explains that:
(1) between 1963-76 Russian nuclear charge designs were mastered for cheap factory mass production (serial production).
(2) the very high yield 1961-2 Russian nuclear tests of 20-50 megatons yield far exceeded the practical weight for missile warheads that could be delivered by affordable missiles, and when both Russian nuclear weapons labs (Sarov and Snezhinsk) tried to scale those designs down to give ~1 megaton from 300-500 kg mass, the results (quote from page 538 follows, emphasis added): "in 1961-1962 were not crowned with success and this worried the military and the developers themselves. It turned out that it is easier to create powerful charges [20-50 megatons] than less powerful [~1 megaton] ones, that have a weight restriction [300-500kg mass]." Reports in recent years however indicate that President Putin has brought back into production the 1961 designs for the tested 50 Mt (lead fusion capsule pusher) or untested 100 Mt (natural uranium fusion capsule pusher) version, to be used in his 32 Kanyon or "Ocean Multipurpose System Status-6" 24 m long, 2 m diameter, 100 ton nuclear underwater torpedo submarine drones, propelled by a nuclear reactor at up to 100 knots, with an operating depth up to 1000 m. This was announced by Putin on 1 March 2018 (below).
(3) To make progress with compact ~1 Mt warheads for missiles, they improved the fission primary stage designs, testing plastic explosive for implosion for the first time in February 1964, and then "octogen" (known in the West as the explosive HMX) for the first time by Russia in the 280mm diameter calibre nuclear shell tested on 19 October 1966 (Russian nuclear test 256, yielding 55kt), which "more than doubled" (page 545 quote) the yield of that device, due to the greater core compression achieved by using a better chemical explosive. This is also of course of great importance to Russian thermonuclear weapons of higher yield, since more efficient primary stages release more x-rays and therefore enable greater fusion charge compression, giving a more efficient fusion burn.
(4) They also improved the fusion charge design radically in 1965 by inserting tritium-deuterium gas into the hollow core of their fusion capsule (i.e. boosting the fusion capsule for the first time), which both improved the efficiency of their thermonuclear weapons, and also made possible cleaner devices (with greater fusion capsule compression due to their improved primary stages, they could replace a fissile spark plug neutron source inside the LiD charge with neutrons from tritium + deuterium fusion, which then fission lithium in the surrounding solid LiD, producing more tritium), allowing the testing of the cleanest ever 140 kt Russian thermonuclear test at Semipalatinsk on 10 December 1972, which had fully 10 times lower fission product radioactivity than the earlier similar 140 kt total yield (of which about 6 kt was fission) relatively clean test of 15 January 1965 at Chagan River (these data are from pages 541-542). In other words, they achieved well over 99% fusion yield (under 1% fission) in their 10 December 1972 test of 140 kt total yield (illustration of Russian >99% clean bomb design is shown below)!
(5) In the later chapter, "Exploding Deuterium", Litvinov clarifies that although Russia failed to directly initiate with PHYSICALLY SEPARATE fission stages the fusion of pure deuterium in its nuclear weapon tests, Russia succeeded in pure deuterium fusion, provided that the deuterium charge was ignited by prior fusion from a larger mass of deuterium + tritium. See also the data from Russia linked here, here, and here. (America never succeeded in initiating a fusion burn in a PHYSICALLY SEPARATE deuterium charge either, despite many entirely false claims to the contrary, alleging that the 1952 Mike test used a fission bomb to compress and heat a completely physically separated charge of deuterium. This is false because the Mike fusion charge was not physically separate from fissile and fissionable material but in contact with both; it had a fissile "spark plug" core inside the deuterium flask, and a fissionable natural uranium pusher on the outside of the deuterium flask; it would not have ignited otherwise as is simple for even a kid to see from the numbers: for the 1-10 keV range of x-ray energies from a fission bomb, and the fact that D-D fusion cross sections for energies of concern are about 1% of D-T cross sections, plus the fact that it was a struggle to get 35% fusion efficiency in the later Castle shots using D+T fusion even with a fissile spark plug and a natural uranium pusher, Mike would have fizzled without the deuterium charge having a direct non-separate fission energy input from within and outside.) In other words, in clean weapons, Russia can boost the total energy from expensive T+D fusion by adding a smaller additional stage of cheaper pure deuterium fuel without the spark-plug and uranium pusher America used in Mike; this smaller deuterium stage size compensates for the fact that pure deuterium requires a higher burn temperature. Naturally, once you have achieved a small very-high-temperature deuterium burn in a small mass (a very hard job and impossible to do directly with a fission bomb, as proved by the true nature of Mike as distinct from lying "simplifications" by those who want to trivilise the problems of warhead design to ban testing for improvements), you can then try to kindle into a bigger volume burn by multiplying up steadily via a large number of "Russian doll" stages (bombs within bombs), gradually increasing the power.
ABOVE: the 82 tons Mike top, in photos during assembly, is covered by a flat disc until Halloween 1952, when the Sausage's Dewar flask inside is filled with liquid deuterium, the fission primary is then inserted on to the top, and the flat cover disc is replaced by the founded top x-ray reflector over the primary. Photos are from Dr Frank H. Shelton, whose friend Dr Alvin C. Graves (who accompanied Shelton on his trip at Penney's invitation to the Australian-British nuclear tests at Maralinga, Operation Buffalo, in 1956) explaining how the primary, sparkplug (kindling), deuterium (fuel logs) and uranium pusher (hohlraum) in the Mike shot works on page 5-43 of his Reflections of a Nuclear Weaponeer (2nd edition, 1990): "First you need a match to start the fire; we use a fission bomb called the primary. Next, you wouldn't try to use the match to set one of the logs on fire, you would use some kindling [the central fissile spark plug]... That is Teller's 'New Super Bomb' invention ... Now you've got your logs burning ... You need a ... kind of furnace, the Germans call this a hohlraum, that propagates the fire ..." This is a very convoluted, pathetically expensive and low-efficiency dead-end in nuclear weapons design, one that has created a Western impasse of "correct" dogma that Russia has broken down! Tragically, we don't just have a nuclear shelters "gap", or tactical neutron bombs "gap", we also have fundamental, massive "gap" in warhead design.
ABOVE: Ernest O. Lawrence with his colleagues from what is now called Lawrence Livermore National Laboratory, at Bikini Atoll in May 1956, preparing for their 3.53 megatons 85% clean (fusion) Livermore Redwing-Zuni test to make thermonuclear weapons fallout-safe as a deterrent (from Dr Frank H. Shelton's Reflections of a Nuclear Weaponeer, where Shelton called the most thoroughly fallout-documented test in history (as a result he testified that fallout was completely safe, see the 10 May 1957 New York Times article below, although he was unfortunately prohibited from PROVING IT PUBLICALLY due to SECRECY nonsense - Shelton being responsible for organising this). Livermore was outdone by Los Alamos, which fired Navajo, a 95% clean 4.5 megatons hydrogen bomb without the fissile spark plug that accounted for 10% of Zuni's 15% fission yield. Los Alamos used plastic foam to slow down the x-rays, giving enough time for primary stage neutrons to be channelled through the hollow centre of their lithium-6 deuteride Sausage, fissioning enough lithium into tritium prior to x-ray implosion. Zuni and Navajo were both rendered obsolete by Lawrence Livermore's John H. Nuckoll's 99.9% clean isentropically compressed pusherless nuclear tests at Christmas Island during Operation Dominic in 1962, the "Ripple" breakthrough (discussed in detail later in this blog post), and by Russian nuclear weapons development tests allegedly "peaceful" but in reality tactical neutron bombs, lasting a quarter of a century (from 1965 onward). On page 8-15, Dr Shelton points out that at the White House's 24 June 1957 Presidential Briefing propaganda event on "clean bomb", only the Livermore Radiation Laboratory designers of 85% clean Zuni were present (Ernest Lawrence, Mark Mills - drowned at Eniwetok in a helicopter crash during a rainstorm while preparing a clean bomb for testing the next year - and Edward Teller): "Conspicuous by their absence from the Presidential briefing were the Los Alamos weapon designers. After all, it was the "clean" [95% fusion] NAVAJO shot on Operation REDWING (1956), designed by LASL, that established the state-of-the-art in reduced fission weapon designs. 'We now believe that we know how to make virtually clean weapons, not only in the megaton range, but all the way down to small kiloton weapons,' Lawrence told the President." Shelton adds on page 8-16 that he briefed the Gaither Commmittee on 31 July 1957 on fallout, which led to the first recommendation for identifying US fallout shelters (ignored by Eisenhower but later implemented by Kennedy).
The gigantic advantage of deuterium fusion is that you don't need to create a large number of neutrons ahead of fusion to fission lithium in order to produce tritium. Lying simplified pictures of nuclear warheads with lithium deuteride secondary stages, often also showing a neutron shield to prevent neutrons from the primary stage from "pre-initiating" the secondary stage (regardless of whether the secondary stage contains fissile material or not) omit the entire problem that lithium deuteride must be irradiated with neutrons to produce tritium prior to D+T fusion becoming possible (otherwise you have no tritium). The 85% clean 3.53 megaton Livermore Zuni test of Operation Redwing at Bikini Atoll in 1956 contained a fissile sparkplug which accounts for about 10% of the 15% fission yield (Zuni contained a lead pusher around the lithium deuteride instead of natural uranium), but the 95% clean 4.5 megaton Los Alamos Navajo test of that series had an entirely clean second stage (no fissile spark plug). But Navajo had to eliminate the neutron interstage shield (unnecessary if you use non-fissile secondary stage) and to use a neutron channel to guide neutrons from the primary stage into the hollow cylindrical lithium deuteride secondary stage, to enable some of the lithium to be fissioned to produce tritium, BEFORE the secondary stage was compressed by x-ray ablation of the lead pusher on the outside of that secondary cylinder. So Navajo needed to have a significant primary yield to release those neutrons, and the design would fail if its primary stage size was reduced to try to reduce fission yield to below 5%. So to make further progress on cleaner weapons, you need either immense, isentropic compressions of the secondary stage that allow neutrons from a non-fissile D+T spark plug within lithium-6 deuteride (or natural lithium deuteride, in the best designs) to work, which has the problem of the radioactive decay of the tritium, or you must consider overcoming the hurdle of D+D fusion to achieve a long-shelf life clean nuclear warhead that doesn't require top ups to compensate for the 12.3 years half life of tritium. The key issue with D+D fusion is that, having a cross section 100 times less than D+T fusion, you need to use isentropic not shock compression to concentrate a lot more x-ray energy into compressing it to extremely high density to get really efficient fusion. But having done so, you then have the advantage of a very clean, very cheap, very long-shelf-life bomb:
Boris Litvinov's "Exploding Deuterium" chapter also examines the use of uranium-233 in nuclear weapons, which is made in reactors by irradiating thorium-232 with neutrons. There is an important storage problem, since Litvinov states that this uranium-233 is contaminated by 0.1% uranium-232, which has an alpha decay chain which includes thallium-208, which releases high energy 2.6 and 0.6 MeV gamma rays, so that a year after production, a mass of 1 kg of U233 or 1 g of U232 gives a gamma dose rate of 10 R/hour at 50 centimetres distance. This makes U233 weapons very difficult to service safely! However, Russia used U233 in place of plutonium in its RDS-37 aka "Joe-19", the Russian's celebrated 1.6 megatons, 22 November 1955 two-stage thermonuclear weapon, according to Dr Frank H. Shelton's Reflections of a Nuclear Weaponeer, page 7-27, which cites reference 24 on page 7-68, which is the Top Secret classified 20 February 1956 U.S. Joint Chiefs of Staff, "Intelligence Information for Joint Intelligence Committee", which says that the RDS-37 fallout contained evidence of U233, U235, U238 and LiD, but no plutonium! I'm just quoting here, and am curious as to how they could rule out the presence of plutonium when of course neutron capture in the U238, which definitely was present, yields U239 which quickly decays into Np239 and then into Pu239 within days! You also get smaller quantities of higher mass isotopes of plutonium, from multiple neutron captures in U238. Maybe they had big samples of fallout and excellent radiochemistry, and deduced that all the plutonium present in the fallout was the result of neutron captures in U238, and none had been present initially in the bomb before firing. If so, hats off to them!
ABOVE: the 1966 Top Secret US Joint Chiefs of Staff report, Study of National Security Factors in a Comprehensive Test Ban Treaty, Appendix C, "Criticality of Nuclear Testing to US Nuclear Weapons Technology", Annexes A and B called for vital long-term improvements to US nuclear weapons designs, including reduction of U235 (oralloy) and T (tritium) dependence, e.g. with efficient isentropic compression of pressurised D capsules replacing T+D, and also enhanced prompt gamma ray weapons for maximising EMP strength (this is done by putting a nickel-chromium shell around the fusion capsule in a neutron bomb, to convert a fraction of the neutron energy into high energy gamma rays). These lengthy annexes also called for reduced warhead costs, increased warhead shelf-life, directed X-ray output (i.e. simply putting the bomb into a metal tube, open at one end, before the development of nuclear pumped x-ray laser Excalibur by Livermore a decade later), enhanced ground shock warheads (e.g. hardened earth penetrator warheads), and reduced fission yield at low total yield to allow cleaner tactical warheads.
(6) A 2005 film (embedded above, and linked on YouTube here) by the Snezhinsk nuclear weapons lab about their nuclear weapon "products" (extensive stills from this film are reproduced below, showing the range of nuclear missile, bomb and cannon shell warheads they developed) adds further information on how Russia managed to reduce the weight of its MIRV nuclear warheads. Translating from the Russian voice narrative commentary of the film: "a Russian patent was obtained for the design of the [thermonuclear weapon casing or] container by the specialists of the two institutes under the leadership of Petrov. In close cooperation with the Institute of Superplasticity of Metals, the city of Ufa, a new technology was developed for manufacturing multi-profile parts from hard-to-form alloys based on nickel-titanium and aluminum using the effect of superplasticity. ... the new technology makes it possible to reduce the weight and increase the strength of parts, and for their manufacture to use hard-to-deform superalloys. ... Product 244 was the first mass-produced atomic small-sized bomb for equipping front-line aircraft weighing 55 times less than the mass of the product 202. Product 245 was the first mass-produced thermonuclear bomb for equipping strategic aviation weighing five times less than the mass of the product 202. When creating products 244 and 245, conceptual provisions were developed for the development of single bombs for a wide range of carrier aircraft ... more than 20 samples of aerial bombs of various calibers were developed and designations for creating a family of them were awarded the State Prize of the USSR. Product 6 was a nuclear warhead of an anti-aircraft guided missile ... Product 30: this is the first development by the Institute of Nuclear Ammunition to equip the ground-based missile system UR-100 ... Product 269 is a nuclear warhead of an operational tactical single-stage missile ...
"The presented nuclear munitions of the missile systems of the navy allow us to trace the origin and development of the least vulnerable naval component of the country's strategic nuclear forces of the product 255a 13 nuclear munition of the R12 missile with a detachable warhead of the D2S complex. ... Product 3 combat equipment of the R21 missile with a detachable warhead of the complex 24, the first domestic complex with the launch of a missile from a submerged position. ... Product 15 combat equipment rocket R27 medium range ... Product 42 combat equipment of the R27 missile to the complex was intended to destroy aircraft carriers and electronic missile defense systems of a potential enemy. Product 46 ensuring the stability of ammunition, the operation of electronic countermeasures and air shock in the conditions of Western firing, the creation of ammunition 46, ensuring the effective use of the T9 complex. Products 82 and 83 combat equipment, the R-27 missile, the first missiles of the naval fleets that could be equipped with both monoblock main part of the v82 nuclear weapon and those sharing the main part with three nuclear weapons of type product 83. ... The ammunition 82 automation system was improved compared to the automation of ammunition 15 and 46. ... Products 94 and 95 were developed for the value of the first complex of the methodological purpose of the navy of the 3rd generation; this can be equipped with a single-block nuclear warhead 94 or divided main and part of the firing of warheads nuclear ammunition 95 individual targeting at specified trailer points. ..." (For clear photographic definitions of the various "Product" numbers assigned to Russian nuclear warheads, see the stills from their film summarising their warheads, below.)
BELOW: a declassified data summary of a wide range of Russian nuclear weapons, their designers, and the use of the weapons by various delivery systems from the VNIIFT nuclear warhead design laboratory, which designed 100% of the currently stockpiled Russian strategic freefall nuclear bombs, and also 100% of currently stockpiled Russian tactical nuclear warheads (both freefall aircraft delivery bombs and artillery fired projectiles of various kinds). This film concludes with the message: "Postscript: In the real conditions of Russia's current position in the world community, and the state of the Russian army, Russia's nuclear weapons remain a reliable guarantor of strategic stability in the world, independence, integrity of the country's military and economic security. - From the (VNIIFT nuclear weapons lab) authors."
The film stills above taken from the 2005 film dedicated to the 60th Anniversary of the USSR's Victory in WWII, made by the VNIITF Russian nuclear weapons design laboratory at Snezhinsk, and it summarises the warheads, their purposes, delivery systems, uses, designers, philosophy, and so on. Note that one of the weapons designers shown to be responsible for the 1970s MIRV narrow-diameter Snezhinsk nuclear warheads (Product 83 with a mass of 170 kg was tested on 2 November 1972 yielding 165 kt, and Product 95 with a mass of 210 kg was tested on 23 July 1973 yielding 212 kt) is Vladimir Fyodorovich Grechishnikov (1917-58), who died in 1958; the point is that the dual-linear implosion primary design of thermonuclear weapon (simply a pipe with two melon-shaped linear implosion fission bombs in it, separated by a capsule of fusion fuel) was developed by 1958, earning Grechishnikov a Lenin Prize. Grechishnikov, a design engineer, had earlier appropriately worked on other straightforward and low-cost solutions for Russia, namely designing the cheap, easily manifactured, but efficient tank and aircraft engines during WWII that helped Russia win decisive battles by numerical superiority. The hard fact that the laboratory credits him with the MIRV warhead designs of the 1970s, despite his death in 1958, proves that the dual primary design first tested in 1958 was used in those 1970s MIRV warheads. Grechishnikov's background in Russian tank designs of WWII is not an aberration of Russian nuclear weapon design, witness that in "Designer N L Dukhov and his School" published in 2004 by JSC South Ural Publishing House, Chelyabinsk, Dukhov is another similar, WWII Russian tank designer who ended up a nuclear weaponeer, deputy chief designer of KB-11 (aka Arzamas-16, or Sarov) developing over 10 years the neutron initiators for the first generation of Sarov's deployed nuclear weapons across 17 delivery systems including the R-7 missile and the T-5 nuclear torpedo!
The weapons designer with the big eyebrows in the film, shown both as a designer of the world's smallest diameter nuclear artillery shell and with President Putin on the latter's visit to the lab by helicopter in 2000, is the late Boris Vasilievich Litvinov (1929-2010), a prolific author of scientific papers and also books hankering after the restoration of Russia as a great power. Russia's version of Edward Teller. In 2019, a 506-page book of tributes to his work was published in Russia, "BORIS LITVINOV: FACETS OF PERSONALITY", published in 2019, which begins with the following quotation from Litvinov: "By the way, a bomb designed for rapid self-destruction, makes it easier to create long-term useful technologies." (VNIITF also has a 1 hour recent film about him on their website, quoting his political books, with his colleagues talking how he remembered the German attack of 22 June 1941, how Russian victory in the war led to progress, and prestige now needs to be restored following the tragic break-up of the USSR. You get the idea...) Boris Litvinov is one of the four authors of the article "History of the nuclear weapons industry" in the Russian journal Atomic Energy, Vol. 86, No. 6, 1999, pages 402-410), which states:
"The creation of the nuclear weapons industry in the Soviet Union is correctly considered as one of the greatest achievements in Russian history. It has been accompanied by the defeat of fascist Germany and space flights to constitute the Soviet Union as a superpower. ... The stocks of uranium (100 tons) accumulated in Germany passed to Soviet physicists in 1945 and were used to construct the F-1 reactor in Laboratory No. 2, which was the first such reactor in the USSR and in Eurasia. ... 31 theoreticians ... participated in various ways in the work on the RDS-37. ... The energy release was 1.6 Mt of TNT equivalent. The USSR was ahead of the USA, which tested a similar thermonuclear aircraft bomb half a year later on May 21, 1956. ... In 1956, NII-1011 had obtained a commission to develop an aircraft bomb containing a gigantic thermonuclear device ... mass about 25 tons. The bomb should have been dropped for bombardment purposes by M-2 and Tu-95 aircraft. Design studies showed that such a bomb could be carried to the target only by the Tu-95 after its bomb bay and framework had been modified provided that the dimensions were reduced to 1.8m in diameter and 8m long with a mass of not more than 25 tons. NII-1011 in 1956-8 worked on the design of that bomb and performed theoretical calculations on the thermonuclear device, but in connection with the moratorium on nuclear tests, manufacturing the body parts was halted, and the only body remaining after the summer tests was destroyed. The work on the device was halted. Nuclear tests were renewed on September 1, 1961. A body was prepared for the gigantic bomb. On October 31, 1961, the world's largest thermonuclear device was exploded above Novaya Zemlya, which had been developed at KB-11 under Sakharov's direction. It was designed for a total energy production of 100 Mt of TNT equivalent, and the device was tested at a height of 4000 m for half the energy production in order to reduce the radioactive contamination of the atmosphere and the effects of the shock wave. ... Somewhat later, a similar thermonuclear device yielding 20 Mt was proposed by KB-11. Out of the gigantic devices tested, only two were adopted as weapons and were for a certain time part of the strategic rocket armament: one developed by NII-1011 and the other by KB-11. ... With the start of reform, the attitude of the country's government to nuclear weapons began to change. The nuclear weapons industry attained its apogee at that time. It was apparent that its experts could resolve any problem in supplying nuclear weapons to the Soviet army although there was an ongoing and considerable lag in Soviet computing behind American."
ABOVE: 30 August 2000 Secret CIA Intelligence 23-page technical Memorandum, "Evidence of Russian Development of New Subkiloton Nuclear Warheads", now declassified with deletions at https://www.cia.gov/readingroom/docs/DOC_0001260463.pdf states that these 0.3 kt tactical/battlefield (so-called "non-strategic" in the obfuscation jargon popular with disarmers) nuclear warheads "blur the boundary between nuclear and conventional war ... as an 'asymmetric response' to US superiority in conventional weapons [e.g., Russian 0.3 kt nuclear weapons will be used when they run short of conventional weapons in the ongoing Ukrainian war, as the West replenishes Ukrainian conventional weapons to enable it to destroy Russian conventional arms]. According to Sergei Rogachev, Deputy Director of the Arzamas-16 nuclar weapons design laboratory: 'Russia views the tactical use of nuclear weapons as a viable alternative to advanced conventional weapons'." Note that these tactical Russian nuclear weapons originated, like the American neutron bomb, from early efforts to produce peaceful nuclear explosives for purposes such as space travel (e.g. American "Project Orion", led by Theodore Taylor and Freeman Dyson, employing Lawrence Livermore's relatively clean, i.e. low fission yield and high fusion yield nuclear warhead designs Dove and Starling, which had little fallout but a huge 14.1 MeV neutron output, motivating Sam Cohen to propose using them for military deterrent purposes in W66, W70 and W79 enhanced neutron output devices), and in this peaceful project "coincidentally", Russia tested a similar 0.3 kt tactical nuclear weapon 900 m down the Ukrainian coal mine at Yumkom, Donetsk on 16 September 1979 (allegedly for "safety" to expel methane gas from the mine - which resumed operation the next day - but such tests also provide military data for use of atomic demolition munitions - ADMs - without violating the 1963 Atmospheric Nuclear Test ban Treaty).
William J. Broad wrote in his 5 February 2022 New York Times article, Ukraine Gave Up a Giant Nuclear Arsenal 30 Years Ago - Today There Are Regrets (contrary to disarmament scammers): "At the end of the Cold War, the third largest nuclear power on earth was not Britain, France or China. It was Ukraine. The Soviet collapse, a slow-motion downfall that culminated in December 1991, resulted in the newly independent Ukraine inheriting roughly 5,000 nuclear arms that Moscow had stationed on its soil. [Along with the nuclear civil defense underground shelters which have allowed the civilians to survive the invasion and fight back, which were fortunately not also destroyed on the say-so of the anti-civil defence journals Scientific American and Bulletin of the Atomic Scientists.] The removal of this arsenal often gets hailed as a triumph of arms control. Diplomats and peace activists cast Ukraine as a model citizen in a world of would-be nuclear powers. But ... both Ukrainian and American experts questioned the wisdom of atomic disarmament. The deadly weapons, some argued, were the only reliable means of deterring Russian aggression. ... “We gave away the capability for nothing,” said Andriy Zahorodniuk, a former defense minister of Ukraine. Referring to the security assurances Ukraine won in exchange for its nuclear arms, he added: “Now, every time somebody offers us to sign a strip of paper, the response is, ‘Thank you very much. We already had one of those some time ago.’” [Idealists will never be able to understand that trash lies written on paper as treaties or agreements are as worthless as trash speeches and acted handshakes in front of TV cameras. Hitler signed endless such treaty lies and also similarly gave endless lying peace speeches and peace handshakes before his invasions and genocide, as did Stalin and all the other dictators. The media of the 1930s lapped it up then as peacemaking, as it always does.]"
From Anthony Loyd, Kyiv, "Veterans of Kyiv rue the day they gave up their nuclear arsenal", Friday February 11 2022, 3.00pm, The Times: "The general who had his finger on the button warns: Don’t give up your missiles. ... tritium boosters and fragments of SS-24 “Scalpel” rocket launch systems on tabletops, all that is left of Ukraine’s nuclear missile stockpile, once the third largest in the world, as workmen began to box them, taking them away into storage in preparation to close the office for good. 'I knew deep in my soul that we should never have given them away' ..." - https://www.thetimes.co.uk/article/step-into-the-twilight-world-of-ukraines-forgotten-nuclear-silos-ljt9g3dh8 (Only one nuclear SS18 ICBM base now remains in Ukraine, 25km north of Pervomaysk, but it is now just a tourist museum, since all of the nuclear warheads have been removed from the remaining four SS-18 ICBMs on display.)
"In terms of volume and breadth of coverage, the program of physical experiments VNIITF has no analogue among all the world's nuclear weapons centers. Of particular importance was a physical experiment conducted in 1965, in which thermonuclear combustion of gaseous deuterium and gaseous deuterium-tritium mixture was carried out. This experience marked the beginning of the development of a new type of atomic charges, the use of which in thermonuclear munitions made it possible to significantly reduce their dimensions and mass, which was very important for the creation of multiple warheads of missile systems, both ground-based and underwater-based. Its results were also in demand in the creation of nuclear explosive devices (NED) for peaceful applications. Peaceful Use of Nuclear Explosions Eugene Ivanovich paid special attention. Under his leadership, VNIITF became a leader in development and use of devices for peaceful nuclear explosions: from the conducted in the USSR 124 peaceful nuclear explosions in 75 development devices were used VNIITF. ... The experience of 1965, in the development and implementation of which Evgeny Ivanovich took personal active participation, was useful for both types of NED. ... Works performed by VNIITF under the scientific supervision of E. I. Zababakhin were marked by high government awards: received 10 Lenin and 20 State Prizes, 4 employees of VNIITF became Heroes of Socialist Labor, many employees received orders and medals of the USSR." Page 15 adds: "In recent years, the VNIIP team under the leadership of E. I. Zababakhin has been actively involved in search of ways to reduce fragmentation [fission fragment residual radioactivity] activity in special atomic and thermonuclear charges of high purity, intended for overburden work. To extinguish a flowing gas well under the guidance and directly with the participation of E. I. Zababakhin, a special small-caliber atomic charge was created."
ABOVE: first Russian MIRV for SLBM was 170 kt yield, 170 kg mass warhead (1974); the first Russian MIRV for ICBM use was a 210 kt yield, 210 kg mass warhead (1978). Both of these signify the 1 kt/kg limit achievable for the small-diameter MIRV warheads (2 MIRV's in the SLBM missile, 3 warheads in the bigger ICBM), using the dual linear-implosion Russian thermonuclear design. However, Russia had earlier put 1 megaton 650 kg, i.e. 1.5 kt/kg "monoblock" (single warhead) on SLBM's in 1974. The design here was more efficient, since it used two spherical primary stages (one on each side of the central thermonuclear charge), rather than two linear-implosion primary charges around the thermonuclear charge which had to be used in the later, smaller-diameter MIRV warheads. All of these weapons employing two primary stages were less "efficient" than the single-primary two-stage Western designs, but they had advantages to Russia in terms of the reduced cost and complexity. (In WWII, cheap Russian tanks overrun more costly German Panzer tanks, because of their sheer numerical superiority: Russia could afford to employ several of their cheaper tanks to destroy one Panzer. Having two primaries means you can use simpler, cheaper primary stages, that don't require boost gas, etc. Russian warheads are mass-produced, unlike hand crafted Western devices. It is the Ford Model-T versus the Rolls Royce Silver Ghost. Which made the most impact?)
ABOVE: this book, RFNC-VNIITF in the Development of the atomic artillery of the USSR, is available online in full here: http://elib.biblioatom.ru/text/kiryushkin_rfyats-vniitf-atomnoy-artillerii_2011/go,0/. Published in 2011, it confirms the secret CIA report from 2000 which gave evidence that Russian work in the 1960s on cleaner peaceful low-yield (subkiloton) small-diameter dual linear-implosion devices compressing levitated pushers with gaseous thermonuclear fuel (tritium and deuterium) was combined with tactical nuclear weapons for military use by the RFNC-VNIITF based in Snezhinsk, Russia. Such devices may well be more efficient as neutron bombs than the USA's single-primary W79 enhanced neutron weapon, which was 0.8 kt fission and only 0.3 kt fusion (if the removable D+T capsule was inserted; if not it was just a pure fission 0.8 kt linear implosion shell). Please also see this book on the assembly of the 50 megaton RDS-202 test design, again in Russian, giving further details of the general approach to nuclear warhead design by Russia, showing on page 38, chapter 4 section 4.1, "Assembly of the main module", that Tsar Bomba 50 megaton bomb's fusion charge was a hollow sphere (of Li6D) with section 4.2 indicating that it had a composite core (e.g. U235 and Pu239) fissile sparkplug (illustrated below): http://elib.biblioatom.ru/text/kiryushkin_kuzkina-mat_2015/go,0/?bookhl=
ABOVE: latest declassified information on design of the 1961, 50 megaton RDS-202 Tsar Bomba shows it contained a central hollow sphere made up of lego like pentagons of lithium deuteride which has to be assembled by a worker stamping on them in slippers (inside each huge hemisphere), and contained a central 500 kt hollow composite core spark-plug (to fission the lithium in the compressed Li6D to give tritium for fusion). This better accounts for the actual weight of the device than a solid central sphere, and also explains the 2-3% fission yield better. Two "pear-shaped" 1.6 Mt 1955 two-stage RDS37's were scaled down to 500 kt each, to act as initiators of the main charge in 50 Mt RDS202, irradiating its pusher from both sides. (The discussion of evidence declassified of this design later in this post will, for simplicity, omit the details of the hollow central spherical fusion charge and its fissile core.)
ABOVE: the original 6 June 1956 report on the design for a 25 ton air drop test, RDS202, had a predicted yield of about 38 megatons and was a derivative from the two-stage RDS-37 test of 1955. It was postponed (not cancelled) by a request on 16 May 1957, owing to successful tests of products 245 and 205, and the final test of the approximately 25 ton bomb in 1961 employed an improved double-approach system suggested by Trutnev and others which was capable of increasing the yield by a factor of about 2.5 from the RDS-37 single-approach principle (first tested in 1958), due to its better x-ray coupling efficiency for main fusion charge compression. However, the 1961 test was only 50 Mt not 100 Mt, because it switched the U238 pusher to lead to reduce the fallout and the blast effect.
ABOVE: 40 kt RDS4 Russian test, air dropped and detonated 350m above the Totskoye, 14 September 1954, in WW2 hero Marshall Zhukov's exercise of 45,000 Russian troops in tactical nuclear war (copying America's Nevada "Desert Rock" nuclear tests with troops in trenches near GZ). A whole book has been published about the radiation effects from this test, showing that the gamma radiation was 140 R/hr at 30 minutes, at 200 m from ground zero, decaying to 0.8 R/hr at 24 hours, and that a peak fallout gamma dose rate of 100 mR/hr occurred 1.5 hours after burst 70 km downwind, where the fallout pattern was 23 km wide. (These are useful data to have, since Russia has not yet openly published anything like America's DASA-1251 fallout patterns compendium.) This is relevant to the whole question of whether Russia really thinks it can use tactical nuclear weapons for military objectives in a limited war: it has actually done the nuclear tests long ago. It is not theoretical!
ABOVE: Russian illustration of American's very inefficient first design of a 15kt oralloy (highly enriched U235) nuclear artillery shell, a total waste of money and materials, as the yield-predicting warhead designer of the first Russian tactical shell explains in his article (discussed in detail later in this blog post). This American design of firing hollow rings of uranium-235 was a very inefficient device. (It is not much better than the design of the gun-type assembly Hiroshima bomb which contained enough oralloy to yield 1 megaton, but was so inefficient it yielded just 16 kt!) More efficient warhead designer Dr Theodore Taylor slammed gun-type assembly weapons as groupthink "committee" designs, based on minimising risks of a misfire, not maximising efficient use of fissile material!)
ABOVE: Russian illustration of a re-design of the America gun-assembly uranium-235 bomb to try to improve efficiency (not by much!). Here, each of the U235 pieces is fired at the other, to reduce assembly time and thus to allow a larger supercritical mass to be assembled before preinitiation risks (fizzle risk) becomes appreciable! American designs are obsessed with minimising risks. Russians are obsessed with maximising performance, efficiency and reducing costs to a minimum (the same approach used with their tanks etc in WWII).
ABOVE: Russian illustration of the first cheap, efficient American linear-implosion plutonium artillery shell, the W48, first put into service in 1963, SEVEN YEARS after the first plutonium linear-implosion Russian tactical nuclear shell was successfully tested with 14 kt yield on 16 March 1956! This American W48 old nuclear shell remained in service from 1963 until 1992, when disarmers withdrew it, allegedly as appeasement, to somehow prevent WWIII via Russia invading Ukraine (or whatever lies are fashionable!).
ABOVE: Russian nuclear warhead designers of the 170 and 210 kt MIRV thermonuclear warheads and the 2.5kt smallest ever diameter nuclear artillery shell (linear implosion), all at the Snezhinsk (formerly Chelyabinsk-70) nuclear warhead design laboratory. They are not as well paid as their American counterparts, but are respected and awarded medals and visits and praise by President Putin (compare faces above to the photo below).
President Putin meeting Russian nuclear warhead designers in 2000, and writing his praise of Snezhinsk nuclear lab's warheads! President Biden, by contrast, campaigned against the nuclear deterrence of invasions, even criticising Donald Trump's modest efforts to convert a relatively few old, low yield W76 Trident warheads into ad hoc tactical warheads four years ago, AFTER Putin had seized Crimea! Duhhh! The Cold War propaganda for Western nuclear disarmament is still going strong today despite all the lives lost in all the wars and invasions that could have been prevented by credible nuclear deterrence since 1992! Tactical nuclear weapons are not regulated by "arms control" liars, so Russia has thousands (precise number UNKNOWN!), and America has zero specifically designed tactical weapons (as we'll see later, the neutron output of low-yield dial-a-yield options on strategic warheads like the B61 are pathetic compared to purpose designed tactical nuclear warheads, so aren't a credible deterrent, a fact covered-up by disarmers). Translation from the 2005 Snezhinsk nuclear weapons film: "In 2000 the President of the Russian Federation visited the All-Russian Scientific Research Institute of Technical Physics. He examined the exposition of the museum of nuclear weapons and left the following entry in the book of honored visitors: The biggest danger facing Russia and the whole world is the violation of the balance of power at the cost of huge efforts and sacrifices to the Soviet. The Union managed to achieve a balance of great merit in this, due to your team together. We are obliged not only to maintain the existing achievements but also to achieve new frontiers relying on the talent and courage of our scientists. With hope and love, Vladimir Vladimirovich, March 31, 2000"
ABOVE: protected underground Russian launch controller centre for SS18 (Satan) ICBM's. Despite the "dead hand" automatic override system (which supposedly automatically launches missiles after a sustained loss of communications from Russian leaders), basic firing is done using relatively simple, low-tech equipment that is hardened against nuclear effects, e.g. resistant to EMP and shielded to give radiation protection against fallout collateral damage. Even if America could knockout such missiles, there is no guarantee that Russia would not - in times of intense crisis such as a US-Russian conventional war - change its basic doctrine to launch them on warning, before American missiles have arrived! Then American warheads would be uselessly blowing up EMPTY SS18 silos! Duh!!
ABOVE: declassified blueprint of Russian nuclear weapon detonator design. Everything they designed was more suitable for cheaper mass production than Western technology, maximising efficiency rather than minimising misfire risks which is the Western idea!
Dr Shirkov, the quantum field theorist who was the yield prediction designer of the RDS-41 tactical 14 kt two-point 406-mm diameter Russian nuclear artillery shell at Sarov, which was tested successfully on 16 March 1956 yielding the maximum possible predicted design yield of 14 kt kilotons, winning him the 1958 Lenin Prize, has a published unclassified article (PDF version of full article linked here) about it online (webpage with summary of article including PDF link to full article is linked here). It was melon shaped, had a U238 reflector, and a thin Pu239 hollow core containing Po210-Be neutron initiator. At Irtysh River in Semipalatinsk, while they were waiting for the wind to stop blowing towards the town, to allow the RDS-41 to be safely surface burst (an air burst would not have created this fallout risk), Shirkov's friend Lev V. Ovsiannikov became interested in the QFT renormalization group functional equations Shirkov was interested in, and solved them, publishing the solution in Proceedings of the Academy of Sciences just three weeks after their nuclear test: https://scfh.ru/en/papers/the-tsar-projectile-for-nuclear-artillery/.
Fellow Russian nuclear weaponeer Vasilii P. Zhogin wrote in his paper, "Development of the First Nuclear Charge RDS–41 (11D) for Artillery Projectile", Combustion, Explosion, and Shock Waves, vol 36, November 2000, Issue 6, pages 689-694 (translated from the Russian version in Fizika Goreniya i Vzryva, Vol. 36, No. 6, pp. 14–20, November–December, 2000): "The result of this trial was so important that the team of implementors with Academician M. A. Lavrent’ev as its leader became Lenin Prize winners in 1958. This Prize was introduced anew and was the second after Kurchatov, Zel’dovich, Sakharov, and Khariton. ... In the U.S., the range nuclear test of the first nuclear charge MK-9 of diameter 280 mm (11 inches) was conducted on May 25, 1953 [the 15 kt Grable shot of Upshot-Knothole in Nevada, which produced no significant fallout despite the fact that its 557.6 ft maximum fireball radius at second maximum thermal output exceeded the height of detonation of just 524 feet, a fact explained by RAND Corp's Dr Kellogg in the 1957 congressional hearings on fallout; the neutron induced Na-24 maximum dose rate near ground zero was only about 10 R/hr at 1 hour and decreased to merely 10 milli-Roentgens per hour at about 1 mile from ground zero!]. ... The [RDS-41] focusing system was developed by V. P. Zhogin. ... Electric detonators were elaborated by M. I. Puzyrev’s team. The neutron source was designed by A. I. Abramov ... a thermostable explosive composition was chosen for use in the charge. After a series of examinations, it was tested on the range of the Central SRI-58 by gun-firing of 2000 37-mm rounds to check their resistance to explosion. ... A test of the RDS-41 charge was planned for March, 1956. The charge enclosed in a projectile was to be placed on the floor of a wooden hut. ... finally the trial was set for the 16th of March ... The equipping operation was delayed for an hour (quite unexpectedly, the aluminum lids of the steel projectile body were jammed, and the projectile body required cooling with snow). ... Some hours later the device was detonated. The results of the test were beyond expectations. The charge exhibited the highest possible power." (Note that the seismic and fallout data at long range led the CIA in its Top Secret NIE report dated 16 May 1962 to wrongly assess this 16 March 1956 Russian nuclear test, "Joe 21" to be 30 kt yield, when in fact the accurate close-in yield determination by Russia was 14 kt. At least the CIA correctly deduced it was a surface burst!)
ABOVE: the world's smallest diameter nuclear weapon is the Russian Snezhinsk lab's 2.5-kiloton 53 kg ZBV3, a 17.4km range, 152.4 mm diameter, 774 mm long artillery shell, shown here with its museum plaque (it is also shown below with the world's biggest ever nuclear weapon - also, you guessed it, a Russian product, in the Snezhinsk nuclear weapons lab instructional museum of warhead design). (For comparison, the smallest Western nuclear weapon, Theodore Taylor's 0.02 kt W54 or Davy Crockett, is 305 mm in diameter, 457 mm long and 26.5 kg. So the Russian ZBV3 is only half the diameter of the W54, but it is twice the mass and of course longer than the W54. There is also a great difference in yield, 0.02 kt for the W54 compared to 2.5 kt for the ZBV3.) The ZBV3 research supervisor was Academician E. I. Zababakhin, the chief designer of nuclear weapons was Academician B. V. Litvinov, and the chief designers of the development of nuclear weapons were L. F. Klopov, O. N. Tikhane and V. A. Vernikovsky. This design began in 1971 and was completed in 1981. Manufacture by mass-production began at the Trekhgorny City Instrument Making Plant in 1981 and was completed in 1991. The special casing it is held in is designed to protect it during storage and transit to the battlefield. It was built to be fired from the widest possible range of Russian artillery: D-20 howitzer guns, ML-20 howitzer guns, 2C3 Akatsia self-propelled howitzers, 2A36 Giatsint-B guns (towed), 2C5 Giatsint-C self-propelled guns.
The descriptive plaque on the bomb in the photo above states (in Russian): "NUCLEAR PROJECTILE. 152 mm CALIBRE. FOR SELF-PROPELLED ARTILLERY INSTALLATION. RFNC - VNIITF [note that VNIIFT = the Snezhinsk nuclear weapons lab design, now part of Pocatom; they have some information on their website about their achievements in developing the best Russian nuclear warheads, stating that they developed the smallest ever nuclear weapon, namely the 152mm one photographed above, the cleanest ever nuclear weapon "in which 99.85% of the energy is obtained through the synthesis of nuclei of light elements", the lighest ever nuclear weapon, and the "the most economical in terms of the consumption of fissile materials", and nuclear warheads capable of withstanding 120C temperature, 750 atmospheres overpressure, and 12,000g's of acceleration on re-entry; maybe we should start buying their nuclear warheads if all this is true]." Snezhinsk nuclear weapons lab also has an interesting webpage about their peaceful nuclear weapons tests here: http://vniitf.ru/article/mirnie-vzrivi "Of the 124 peaceful explosions carried out in the USSR, 80 nuclear charges developed at VNIITF were used in 75 cases. ... VNIITF began to carry out peaceful explosions of its charges from May 1968. ... All developments of NEDs for peaceful purposes were headed, carried out, supported and supervised at VNIITF by Academicians E.I. Zababakhin, E.N. Avrorin and B.V. Litvinov. ... If for peaceful camouflage explosions there were no special requirements for the “purity” of charges, then for ejection explosions (formation of dams, trenches) nuclear explosive devices with a minimum amount of radioactive fission fragments were needed. In these cases, thermonuclear devices are more suitable, in which the main energy release is due to fusion reactions. Such charges were also included in a series of peaceful NEDs developed at VNIITF, and were used to create a trench in the Pechora-Kolvinsky Canal section (Perm Region) - an integral part of the project developed in the 1970s to transfer the waters of the northern rivers to the Volga. The experiment to create this trench was called "Taiga". It was preceded by model explosions of low-power (0.2 kt) nuclear charges in wells at the Semipalatinsk test site (1968) "Telkem-1" and "Telkem-2", where the formation of an ejection funnel (a single explosion, T-1) and a short trench (a group explosion of three charges, T-2) was checked. The analysis of the results of these explosions was used in the design of the main experiment "Taiga". A year after this experiment, an improved “clean” charge was tested at the Semipalatinsk test site with a 5-fold reduced fragmentation activity compared to that used in the Taiga operation. ... In conclusion, we note that VNIITF is, in fact, the only organization in the world that develops specialized nuclear explosive devices for industrial applications."]
ABOVE: In 2015, S. Douglas Woodward's book Is Russia Destined to Nuke the US pointed out that Russia's only real military superiority is in tactical nuclear weapons, the most effective deterrent possible to allow it to invade Ukraine and Europe, since the West has now no way to counter it: "Europe protests the incursion but seems unwilling (and unable) to use military force to push Russia back from its designs on Ukraine and Crimea. ... Then there is the state of the Russian people. They suffer under economic sanctions imposed by Europe and the United States. Backed into a corner, is it suprising Russia rattles its sabre? However, Russia's only sabre - its one area of military superiority, is Russian tactical nuclear weapons [2,000] outnumbering NATOS tactical nukes 10 to 1 in the region. As Russia weakens in critical areas, several factors are converging which suggest Russia must act now ... The February 2014 agreement between Russia, Ukraine, France and Germany (the so-called Minsk Agrement) has failed ... 'During the era of political romanticism, the Soviet Union pledged never to use nuclar weapons first,' Kiselyov told the audience of Vesti Nedeli, his current affairs show ... 'But Russia's current military doctrine does not - no more illusions'."
ABOVE: Russian plans for the tactical use of nuclear weapons (English translation left; original Russian on right), from our 20 September 2017 blog post here, taken from restricted Russian manual Nuclear Weapons - A Manual for Officers, which we obtained from Ukraine and put on internet archive to show the threat. On pages 9-10 of his 1977 book Surviving Doomsday, Bruce Sibley (who in the 1980s edited the UK CD magazine protect and Survive Monthly) pointed out: "During the 1960s, the original lead which America held in numbers of strategic missiles began to show signs of erosion ... Not only were the Russians developing new missiles and warhead techniques, but their whole armament programme began to expand at an alarming rate. At first, Soviet proclamations asserted that this was merely a 'catching up' with America and NATO, but since this expansion has continued aggressively ... it may not be an exaggeration to hold the view that the Soviet Union has now overtaken NATO and American military might ... The matter of civil defence playing a major role in strategic warfare planning ... the 'ace in the hole' ... No country on earth has a civil defence programme as extensive as the Eastern Bloc. ... Unfortunately, the majority of Western politicians and some of their advisors seem quite oblivious to the strategic significance of Russia's preoccupation with a major civil defence programme. They either scorn or remain in ignorance of the facts. Some critics even charge that by its very existence, civil defence makes the prospect of nuclear war more thinkable, and therefore should not be developed. This is an essential part of their package for banning the bomb."
ABOVE: Page 42 of Putin's latest 2014 Russian civil defense manual supporting the tactical use of nuclear weapons (English translation and original Russian test), from our 20 September 2017 blog post here, full manual was put on internet archive to show the threat. Again, civil defense when combined with offensive plans for nuclear weapons is an offensive problem; the opposite is true for purely defensive civil defense (which increases the nuclear threshold by enabling survival of accidental and limited nuclear strikes). On pages 5-6 of his 1977 book Surviving Doomsday, Bruce Sibley pointed out: "Meanwhile, the Soviet Union possesses the largest and most comprehensive war-survival programme in the world today. The Soviet leadership never tires of reiterating that victory is impossible unless every Soviet citizen has undergone intensive practical and moral-psychological civil defence training. ... The Soviet evacuation scheme intends to scatter 241 million citizens throughout the Russian countryside ... urban evacuation is the key to twarting the 'estimated' killing power of nuclear missiles ... the Soviets have maintained vast stockpiles of grain, tinned food, fuel, water, medical supplies, clothing, spare parts and raw materials throughout the USSR ... The entire Moscow underground railway system has been equipped to give protection and life-support to over one million persons. Every Soviet citizen has been issued with a gas mask, that will filter out radioactive dust and chemical and biological aerosol agents ... the Russians may be committed to the downfall of Western ideology - by peaceful subversion or by open conflict." (All of the arguments against this kind of civil defense are specious: Britain evacuated 1.5 million of vulnerable people from London 48 hours before declaring war in 1939, and the Luftwaffe didn't bomb the evacuees or "simply" retarget the dispersed population. Another fallacy is that dispersing millions of people into the countryside will make sanitation and food problems worse. The reality is that sanitation and food supply logistics break down in bombed cities far sooner than in the countryside, where people are nearer food sources! The effect of fast-decaying fallout on crops is trivial.)
ABOVE: major designs of Russian warheads using two primary stages wired in parallel circuit (for explosive detonators on the implosive systems of each primary charge, and also parallel circuit for the later pulse of current to the neutron sources for each primary charge), to produce x-ray ablative linear implosion of a central thermonuclear charge:
These are an alternative to using plastic foam to diffuse x-rays in all directions to allow a single primary stage to compress a spherical secondary stage isotropically, without x-ray shadowing problems. Plastic foam reduces speed and efficiency of x-ray delivery (the recoil ablation force on the secondary, F = dp/dt, is reduced when plastic foam is used to diffuse x-rays, because the longer diffused pulse of x-rays which is delivered via plastic foam has an increased pulse duration, t). For many purposes, therefore, two primary stages for linear implosion of a fusion charge, without needing any plastic foam, is just as an efficient approach as that used in single-primary Western devices.ABOVE: error by DTRA regarding energy absorption by buildings. U.S. Government's DTRA DISPATCH magazine article "Building Effects on Airblast from Nuclear Detonations in Urban Terrain" falsely conflates the abrupt shock front with the length of the entire blast wave, claiming that since buildings are 2000 denser than blast waves: "the air will move 2000 times father than the structure in the same time interval. Thus while the building is moving 1cm. the shock has moved more than 20m, and the energy is a small fraction of 1% the blast energy." The key error here is the statement that "the shock has moved 20 m". They meant the shock front, which isn't the same thing as the entire blast wave, the thickness of which is dependent on bomb yield, and is what moves drag-sensitive buildings with large window openings where the overpressure quickly equalises. So they are totally wrong. They are absurdly arguing that only 1/2000 of the dynamic pressure (kinetic energy per unit volume of air) of air presents a force upon buildings, or presumably upon ships sails (which are denser than air), or eardrums (again which are denser than air). The shoddy, imprecise form of their statement makes it hard to understand precisely what they are saying, but it seems to be that they are assuming falsely that the blast wave consists only of a shock front, which will move 20 m past the building (without moving it significantly) before the building has moved 1 cm, but the density of the building and the location of the shock front relative to the building is IRRELEVANT while the mass of air BEHIND the shock front is delivering energy to the building, as proved by the absence from the relevant equations of both building density and shock front location after it has passed, but winds are still blowing. It's not the shock front that causes the building to oscillate, but the wind pressure behind the shock front. The building density, and the distance the shock FRONT moves beyond the building, have no relevance to thickness the layer of air BEHIND the shock front, which is what is pushing the building, and this thickness increases with bomb yield! (However, most of the push to the building occurs due to the highest dynamic pressure, i.e. the air just behind the discontinuity or "shock front".) As a result, the actual energy absorption by a building is more than 100 times greater than DTRA's ratio of densities claims. Small-scale models of buildings, whether absolutely rigid or made from glass mirrors don't in any way, shape or form model the energy captured in oscillations by thousands of tons of reinforced concrete of real buildings.
The wind (dynamic) pressure induced motion effects which have nothing to do with the relative density of the shock front compared to the building. The amount of energy picked up from either the wind pressure of normal breezes or the blast wave of a nuclear explosion, by a building in oscillatory energy is the time-integrated form of Newtonian equation E = F.x, where force F = P.A, where P is dynamic pressure and A is area, and x is the amount of displacement induced. There's no density of the building in these equations, and no dependence on the shock front, but rather the integrated dynamic pressure over the entire duration of the blast at the location of interest (if the building delays the passage of the shock front instead of letting it pass freely through windows etc, then there's an additional term for the time-integrated overpressure contribution). As dynamic pressure is removed by the building - not by the shock front but by the air behind it, lasting seconds in higher yield detonations - the overpressure also falls as the blast restores itself to the Rankine-Hugoniot conditions (overpressure energy is transformed into dynamic pressure energy, thus weakening overpressure as well as dynamic pressure). If DTRA were correct that only the front part (shock front) of a blast wave is relevant to delivery of energy and delivers only 1/2000 of the energy of the blast, then by analogy our eardrums and ship sails would be similarly so inefficient at picking up energy from the dynamic pressure of sound and the wind, respectively, that they couldn't work! Notice that their computer codes in 2013 falsely EXCLUDED any absorption of energy by the blast in oscillating thousands of tons of reinforced concrete, causing damage (much larger, huge amounts of energy are required to actually destroy reinforced concrete by permanent deformation; the springy oscillations of a building in a gale or blast wave take up far less energy than actual destruction requires), contrary to what John von Neumann pointed out (that buildings are NOT rigid but absorb energy from the blast, decreasing the blast parameters like pressures and impulses as the blast propagates through a city, unlike desert or ocean in unobstructed terrain nuclar tests!) in the 1950 Effects of Atomic Weapons (removed by Glasstone from future editions, just as he removed the civil defence chapter from the 1977 edition!).
ABOVE: Appendix A of Glasstone's 1950 Effects of Atomic Weapons gives a specific calculated example that allows the absorption of blast energy by oscillating modern concrete buildings to be calculated: a reinforced concrete building of 952 metric tons, 75x75ft, 38 ft high (thus horizontal area of 265 square metres), resisting force 4 psi, is subjected to a peak overpressure and dynamic pressure loading of 32 psi (242,000 Pascals) decaying to zero in 0.32 second. Calculated peak deflection of middle of the building was 0.88 foot or 0.27 m (the top would be deflected twice this amount). Reinforced concrete is relatively ductile, but any cracking absorbs even more energy than the simple calculation of the kinetic energy of blast-induced oscillation. So the blast wave energy absorbed from the simple physics law E = Fx = PAx where P is pressure loading, A is exposed area of building being loaded, and x is the displacement(or more precisely from the integral form of this, where energy absorbed is force integrated over displacement, as shown above) is about E = Fx = (242,000)(265)(0.27) = 17,000,000 Joules. This energy is removed from the blast wave by being transferred from the blast into the kinetic energy of oscillating the building! Hard fact!
The resisting force of 4 psi used in the 1950 Glasstone book can be updated with the following static yield resistances for various modern city buildings using Table 15.6 on page 525 of the 1996 Northrop Handbook of Nuclear Weapon Effects: Calculational Tools Abstracted from EM-1: 3.0 psi and 0.3 second natural period of oscillation for 3-8 story reinforced concrete buildings (type 15.2.2), 1.25 psi and 0.3 second for brick houses (type 15.2.3), 0.5 psi and 0.25 second for wooden houses (type 15.2.5), or 2.0 psi and 0.6 second for 3-10 story steel-frame office buildings (type 15.2.10). The "nominal" ductility ratios (the ratios of displacement required for collapse/severe damage to the maximum elastic response before plastic response begins) for these four types of buildings are given by Northrop as 7.5, 4, 7.5 and 10, respectively. The maximum amount of energy absorbed in destroying the buildings is simply the area under the curve of loading versus displacement before collapse. Since this relative area is 0.5 unit for the triangle shaped slope up to a ductility ratio of 1, and is roughly a constant height rectangle for the plastic zone from a ductility ratio of 1 up to the failure limit (severe damage/collapse of building), the ratio of total energy absorbed by a building in its destruction, to the maximum energy that can be absorbed in purely elastic oscillations by a buildings (up to ductility ratio of 1 unit) is simply [0.5 + (7.5 - 1)]/0.5, [0.5 + (4 - 1)]/0.5, [0.5 + (7.5 - 1)]/0.5, and [0.5 + (10 - 1)]/0.5, or 14, 7, 14, and 19, respectively, for those four building types. It is to be noticed that the greatest amounts of plastic range energy absorption are for the most predominant two kinds of modern city centre buildings, namely reinforced concrete and steel frame multistory buildings. These buildings, with up to 8 and 10 stories, respectively, in these calculations, also have a cumulative effect in shielding free-field thermal and nuclear radiations.
The Effects of Atomic Weapons, 1950, on page 57 has a section written by John von Neumann and Fredrick Reines of Los Alamos (it is attributed to them in a footnote) stating clearly: "the structures ... have the additional complicating property of not being rigid. This means that they do not merely deflect the shock wave, but they also absorb energy from it at each reflection. The removal of energy from the blast in this manner decreases the shock pressure at any given distance from the point of detonation to a value somewhat below that which it would have been in the absence of dissipative objects, such as buildings." Glasstone removed this from future (1957-77) editions, not because it is wrong (it isn't), but apparently because it debunks official nuclear lies used for strategic deterrence in the same way that gas and incendiary bombing effects was exaggerated in the 1930s to try to deter war!
ABOVE: The two terms for blast wave energy. It's really very simple: the first term above is the kinetic energy contained in the dynamic (wind) pressure of the blast, while the second term represents the internal energy of the blast (manifested as heat and related static overpressure). So the theoretical basis for the calculation of blast energy absorption by a city is not rocket science, and it's not based on speculations or guesswork. And this is not "new" either, since Brode's 1954 equations for calculating blast wave's with a computer include energy balance, and you can with modern computers easily incorporate the irreversible energy losses due to the blast wave successively oscillating, one after another, the buildings with with it interacts as it travels outward in a modern city. William G. Penney gives the real basis for calculating the energy loss due to blast damage in Hiroshima and Nagasaki in his 1970 paper, which contains numerous detailed, precise calculations and measurements showing how the act of causing destruction to steel and concrete, in addition to the mere oscillations of buildings, reduced the energy content of the blast and thus the pressure fell more quickly with distance in those cities, than measured in unobstructed desert or ocean during his nuclear testing programme. (In 1985 John Malik of Los Alamos simply ignored in his report, LA-8819, all Penney's hard won facts from Hiroshima and Nagasaki, without going into details at all. Glasstone and Dolan reference Penney's 1970 paper, but simply ignore its findings on blast attenuation in Hiroshima and Nagasak. So much for scientific progress! Note also that Penney's 12 kt yield for Hiroshima is lower than the current estimate of 16 kt, implying even more blast absorption in Hiroshima than Penney found, because the unattenuated free field pressures from 16 kt will be greater than those from 12 kt!)
Now consider the energy absorption in the plastic region for reinforced concrete. The calculations of energy absorption in oscillating a building are for the small "elastic response" region of the pressure-displacement curve. But vast amounts of energy are absorbed beyond that elastic limit, and yet at pressures lower than required to make a reinforced concrete building collapse (always ignored by ignorant shelter critics, as Lord Baker explained, for shelter design in his 1978 book which we reviewed in detail a few posts back). There is a summary of the key building parameters America uses in calculating the effects of nuclear blast on buildings of various kinds in Table 15.6 on page 525 of Northrop's 1996 Handbook of Nuclear Weapon Effects, Calculational Tools Abstracted from EM-1: building 15.2.2 (3-8 story reinforced concrete, small window area) has a severe damage ductility ratio of 7.5, i.e. it fails and collapses (severe damage) when the displacement is 7.5 times the maximum elastic response. Put another way, the plastic limit for reinforced concrete is 7.5 times the elastic displacement limit. Northrop's figure 15.7 shows the extension versus applied pressure load. The energy absorbed in the elastic limit is a triangle terminating at a displacement of 1 ductility unit (units are extension/elastic limit extension), so it has an area of 0.5 units (energy absorption for oscillating the building, see diagram below). But the plastic response is not a triangle but a unit high rectangle which starts at one unit and extends to 7.5 units (severe damage/collapse), its area is thus 7.5 - 1 = 6.5 units, so it absorbs 6.5/0.5 = 13 times as much energy as that used to oscillate the building elastically! So reinforced concrete buildings can absorb 13 times more energy in being damaged, than they can absorb in oscillating elastically. The ratio of total energy absorbed to flatten the buildings, to the maximum energy that can be absorbed elastic oscillate it, is (6.5 + 0.5)/0.5 = 14. Thus, the total energy absorption by a building can be 14 times that involved in merely oscillating it!
ABOVE: model of a building having a blast, the simple engineering graph from EM-1 showing the ratio of energy needed to total a building to that which merely oscillates it. The axes depict loading force and displacement, respectively, so the areas under the curve beautifully correspond to energy absorbed, allowing us to calculate the total energy needed to flatten a city very easily (from a simple, standard physics formula, energy E = Fx), in terms of multiples of the energy needed to just oscillate the buildings elastically. Northrop's data for other types of buildings are as follows: type 15.2.5 wood frame house has the same 7.5 ductility ratio for collapse, so it can absorb in plastic deformation 13 times the elastic oscillatory energy; type 15.2.3 brick house has a ductility ratio of 4 for severe damage, and a type 15.2.10 3-10 story steel-frame office building has a ductility ratio of 10 for severe damage. This is precisely Lord Baker's principle of the Morrison table shelter (for details, please see Lord Baker's 1978 book about the problems with explaining this to the bureaucratic nutters who don't understand the physics behind engineering, the brilliantly titled Enterprise versus Bureaucracy) where the plastic deformation of steel is used to absorb many times more energy than it can absorb elastically. In other words, it's the damage done (plastic deformation of reinforced concrete) that really absorbs vast amounts of blast energy, not the smaller energy absorption from elastic oscillations of a building! Northrop's table 15.6 shows that the reinforced concrete building, type 15.2.2, has a natural period of oscillation of about 0.3 second, and a static yield resistance of about 3 psi. Northrop's Figure 15.10 shows it has 50% probability of severe damage at 2.85 km from a 1 megaton surface burst on an ideal, unobstructed desert surface with no blast energy absorption by buildings intervening between that target and ground zero! For comparison, a similar 1 megaton surface burst in unobstructed desert is shown in Northrop's Figure 15.11 to have 50% probability of destroying a typical British brick house at 4.42 km ground range (50% severe damage probability), whereas Figure 15.18 gives a range of only 2.74 km for collapse of 3-10 story steel-frame buildings from a 1 megaton surface burst on unobstructed, open terrain.
In fact DTRA and its predecessors back to General Groves of the Manhattan project have has been covering-up the facts determined at Hiroshima in order to foster a delusion that strategic nuclear bombing against cities can work, despite failing. Anyone can simply move people out of cities (as the UK did with kids in Operation Pied Piper, 1 Sept. '39) before declaring war, and then your entire pathetic "countervalue strategic" anti-city deterrent is flushed straight down the pan! This undermines credible nuclear deterrence, which requires tactical nuclear weapons to prevent the invasions that set off both world wars (Belgium '14, Poland '39). It Ukraine had that it wouldn't be in the situation it's now in. Nuclear disarmament didn't make it safe. DUH! (And no, Mr "Scientific American", Hitler did not send the luftwaffe to bomb the kids being evacuated from London on 1 September 1939!)Professor Bridgman's Introduction to the Physics of Nuclear Weapons Effects can be used to demonstrate the exaggerations in Glasstone's Effects of Nuclear Weapons when Glasstone's free-field (unobstructed terrain) nuclear effects predictions from desert and ocean nuclear tests are improperly applied to concrete cities. Bridgman, for instance, considers a building with an exposed area of 163 square metres, a mass of 455 tons and natural frequency of 5 oscillations per second, and finds that a peak overpressure of 10 psi (69 kPa) and peak dynamic pressure of 2.2 psi (15 kPa) at 4.36 km ground range from a 1 Mt air burst detonated at 2.29 km altitude, with overpressure and dynamic pressure positive durations of 2.6 and 3.6 seconds, respectively, produces a peak deflection of 19 cm in the building about 0.6 second after shock arrival. The peak deflection is computed from Bridgman's formula on p. 304. This 19 cm computed maximum deflection allows us to estimate how much energy is permanently and irreversibly absorbed from the blast wave by a building (if damaged, additional energy is absorbed and is transformed into slow-moving - relative to the shock front velocity - debris which falls to the ground and is quickly stopped after the blast has passed it) by: E = Fx, where F is force (i.e., product of total pressure and area) and x is distance moved in direction of force due to the applied force from the blast wave.
If the average pressure for the first 0.5 second is equal to 12 psi (83 kPa) then the average force on the building during this time is 13 million Newtons, and the energy absorbed is: E = Fx = 13,000,000*0.19 = 2.6 MJ, which is removed from the blast wave in the form of oscillations of the building. Successive absorption by building after building rapidly absorbs blast energy in this way.
Although you could say the blast wave from a 50% blast nuclear megaton warhead contains 2.1 x 10^15 Joules, the blast wave energy rapidly decreases as it dumps hot air behind it to form the fireball (Glasstone omits the fireball energy partition after blast breakaway, but the DELFIC mushroom cloud module shows that, to fit observed cloud parameters theoretically, fully 45% of the yield is hot air dumped behind the blast that powers the mushroom cloud rise and expansion, so 50-45 = 5% of total yield (or 1/10 of original blast yield) remains in the blast wave after the negative phase fully develops). In addition, the blast forms a 3-d hemisphere so that the percentage of the total blast energy in the Mach front intercepting buildings near the surface is small and gets smaller as the blast propagates! It is only that part which causes damage that gets attenuated; furthermore the yield scaling issue increases the building shielding effect for larger yields, because the radial distance being considered is increased. For example, in the example above, 10 psi peak overpressure (69 kPa in SI units) occurs at 4.36 km from a 1 megaton strategic bomb, but the 163 square metres of the building is only a small fraction, f, of the blast hemisphere at that range, namely f = 163/(2*Pi*4360^2) = 163/120,000,000 = 1.37*10^{-6}. So if the blast still contained 5% of the total weapon yield at this stage (1/10 of the original blast yield), the total blast energy striking the building's surface area would be just (2.1 x 10^14 )* 1.37*10^{-6} = 2.9*10^8 Joules, proving that the oscillations of the building removed 2.6MJ of 290MJ blast energy intercepted, nearly 1%, which is a similar fraction to Penney's finding in Hiroshima.
You get additional, greater, energy loss due to damage done to buildings close to the fireball. For n such buildings in a radial line, the cumulative removal of blast energy fraction is: exp(-2.6n/290), which is greater for the larger blast damage distances in built up areas predicted for effects of higher yields! So increasing the yield increases the shielding for any given free-field pressure (the distance of which scales up with yield)!
Even with wooden 1-storey houses predominating in Hiroshima, Lord Penney who took away the overpressure debris (crushed petrol cans, etc) for analysis in England in 1945 found the blast energy at Hiroshima decreased exponentially due to blast attenuation caused by damage done, by comparing his results to the free-field Maralinga desert values for British nuclear tests without a precursor. This was all ignored by Uncle Sam (Glasstone)!
We have already given in many posts extensive evidence proving that concrete buildings in Hiroshima and modern cities absorb thermal, nuclear and blast effects in a way totally ignored by Glasstone's unobstructed desert analysis. Strategic nuclear deterrence is thus bunk, if based on nuclear test effects data from unobstructed desert or open ocean. We need tactical nuclear deterrence to stop invasions and the use of force, not an incredible threat of bombs on cities, which is analogous to the gas and incendiary bombing exaggerations of the 1920s and 1930s which failed to deter WWII. The exaggerations were made by both lying disarmers (to scare people into disarmament) and by lying proponents of aerial bombing in war (to scare enemies into surrender). The resulting pseudo "consensus of expert opinion" from both groups had tragic consequences. Strategic bombing, megatons of ~100 kg high explosive on Germany, equivalent to a large nuclear attack however you scale the megatonnage (by the 2/3 power of blast yield for peak overpressure over unobstructed terrain, or by an even weaker function of yield for initial nuclear radiation), also failed to produce military results when civilians were bombed. The two low yield nuclear weapons dropped over mostly wooden houses in Japan did not produce the results publically claimed (for propaganda) for modern concrete cities. We've been blogging this for years, ignored by the loons who prefer anti-nuclear lies about strategic nuclear deterrence!
So to correct Glasstone for urban areas:
(1). Simply use Lord Penney's exponential attenuation formula from Hiroshima to reduce peak overpressures in cities: exp(-R/3.25) for R being radial distance through a city in kilometres. This reduces peak overpressure by 50% at 2.2 km. (Obviously precise effects depend on details, but this is a "baseline" for minimal blast attenuation, in cities with predominantly wood frame buildings.)
(2). Simply use George R. Stanbury's formula for predicting the thermal flash shadowing, by calculating the number of exposed upper floors that can geometrically "see" the fireball as a function of range, so that the number of computed flash burns correspond to the number of windows that can see the fireball (e.g. for 50 ft wide streets, 3 miles from a 1 megaton surface burst, only the highest floor can "see" the fireball since the angle from the top of the fireball to building top artificial skyline is 13.5 degrees; if the buildings are on average 10 floors high, the percentage burns and fire risk is therefore 1/10 for one side of a building with 4 sides, i.e. 1/40 which is smaller than the 1/10 assumed by some simplistic propaganda; but you then get into the issue of the size of the windows and whether the people inside are protected by shadows from walls or furnishings or internal office cubicle partitions or even other people in between the target and the fireball in the office, all of which reduce the simplistic "theoretical" estimates of the number of people burned, instead of assuming that no buildings or screening exists at all as in anti-nuclear propaganda for so-called "arms control" (war via appeasement/disarmament as in the 1930s). Stanbury points out there, and in his August 1962 Restricted UK Home Office Scientific Advisory branch Fission Fragments article on Fires from nuclear weapons, that to produce firestorms in Germany - the allies tried hard to achieve this in 1943 to end the war (and firestorms produce the associated soot clouds for climatic "nuclear winter" effects hype) you needed 50% of buildings to be initially ignited, which was only possible in the (now burned and gone) medieval wooden areas of Hamburg and Hiroshima (due to blast-overturned charcoal braziers in wooden houses in Japan, not the thermal flash which was obstructed by rooms and other buildings). Stanbury's studies of the thermal flash shielding in Liverpool and Birmingham showed that the thermal radiation is shielded to such an extent you simply can't get to within an order of magnitude of that 50% ignition incidence needed for a Hamburg style intense firestorm (or, therefore, nuclear winter due to Hamburg type firestorm soot clouds penetrating the stratosphere)!
The effect of scattered thermal radiation diffusing into shadows was insignificant at Hiroshima and Nagasaki, where burns from thermal radiation were only received in an unobstructed radial line from the fireball, so that any shielding provided virtually complete protection from thermal flash. The 110 Castle-3 shot at Bikini Atoll in 1954 was fired during a moderate rainstorm to obtain data on the reduction of blast and thermal effects by rainfall. There are no films that show the fireball because the water content of the air absorbed the thermal and visible transmission. Heavy rain or fog absorbs the thermal radiation locally around the fireball, rather than creating a large amount of dangerously wide-angle scattered radiation at great distances. Northrop's 1996 Handbook of Nuclear Weapon Effects: Calculational Tools Abstracted from EM-1, gives data for Pacific test conditions in Figure 6.39 on page 248, on the effect of scattered thermal radiation from a burst at 1 km altitude, at various distances and for different fields of view:
At 10 km ground range, 43% of the thermal radiation in unobstructed terrain is direct (from the fireball), and 57% is scattered, but the angular distribution of scattering is not extreme (most of the scattering comes from air relatively near the fireball): the total (direct plus scattered) is 80% for a 30 degrees field of view (only 20% of the thermal radiation comes from angles exceeding 30 degrees from the radial line to the burst). Only 4% of the total thermal radiation at 10 km comes from angles beyond 90 degrees (i.e. 96% comes from the hemisphere around a target facing the burst).
At 30 km ground range, 16% of the thermal radiation in unobstructed terrain is direct (from the fireball), and 84% is scattered, but the angular distribution of scattering is not extreme (most of the scattering comes from air relatively near the fireball): the total (direct plus scattered) is 70% for a 40 degrees field of view (only 30% of the thermal radiation comes from angles exceeding 40 degrees from the radial line to the burst). Only 6% of the total thermal radiation at 10 km comes from angles beyond 90 degrees (i.e. 94% comes from the hemisphere around a target facing the burst).
Northrop's 1996 Handbook of Nuclear Weapon Effects: Calculational Tools Abstracted from EM-1, also gives graphs of the thermal radiation spectrum, showing differences with burst altitude and yield. Figure 6.19 shows that a 1 kt surface burst gives a thermal spectrum which peaks at 1.1 micron (Planck radiating temperature = 2000 K), compared to 0.4 micron (Planck radiating temperature = 5000 K) for 1 kt air bursts at 1-30 km altitude. Figure 6.21 shows there is much less difference between the spectra for surface and air bursts for 1 megaton yield: 0.70 micron peak in the thermal spectrum (Planck radiating temperature = 3800 K) for a megaton surface burst, compared with 0.52 microns (Planck radiating temperature = 4500 K) for a 30 km altitude megaton burst.
Northrop's 1996 Handbook of Nuclear Weapon Effects: Calculational Tools Abstracted from EM-1, in Figure 16.10 uses hydrodynamic calculations to prove that the maximum fire wind velocity in a firestorm is only a weak function of the fire intensity, for example a fire with a radius of 10 km will create a maximum fire wind velocity of 17 m/s for a fire intensity of 25 kW/m2, but this only increases to 36 m/s if the fire intensity is increased to 240 kW/m2.
Remember also that nuclear test evidence shows that the risk of clothing or other items burning is less for real levels of office humidity than for target materials left to dry out in the Nevada at the lower humidity of Nevada nuclear tests like Encore; clothing shields thermal radiation and increases burns energy requirements contrary to Glasstone.
Northrop's 1996 Handbook of Nuclear Weapon Effects: Calculational Tools Abstracted from EM-1, Table 14.5 on page 501 also points out that while people standing nude 2 metres behind glass windows watching the nuclear blast approach them will receive a 50% median dose of 3 glass fragment abdominal wall penetrations at a peak overpressure of 7 psi, it takes 15 psi if they are wearing clothing! If they duck and cover, they will can avoid the directional flying glass (and the thermal burns) completely. What Northrop doesn't tell you is that in a built up city, the dynamic pressure needed to energise those glass fragments to lethal velocities don't exist 2 metres behind glass windows in general; only behind those windows facing the fireball with an unobstructed view. Other windows on all all sides of the building will certainly break if the overpressure is high enough, but the blast wind (dynamic pressure) is directional and so the windows will not be blasted inwards with the same speed (at lower pressures they can even fail in the negative phase and be sucked outwards, with no hazard whatsoever to occupants!). Northop (1996) in chapter 14 on personnel casualties gives very high mortality rates based on unprotected head impacts, particularly for standing personnel, e.g. 5 psi for 50% mortality for people standing in buildings swept through by blast winds. Again, this assumes the blast winds are not obstructed and attenuated by the other surrounding buildings in a city, but it also suggests a simple civil defense precaution to accompany duck and cover in a crisis situation: bicycle helmets can be kept under emergency table "shelters" and can be put on quickly before the blast arrives, after a nuclear explosion, to minimise head trauma from flying debris or bodily translation and impact for high dynamic pressures and long blast durations. With duck and cover, you can avoid wind drag or injury from flying debris and you can keep away from a blast reflecting surface, then Northop shows in Figures 14.2 and 14.3 that you have 50% chance of surviving 37 psi peak overpressure from 1 megaton if you are lying down perpendicular to the direction of approach of the blast wave, or 62 psi if your are lying parallel to the direction of the blast (i.e., lying down facing away from the flash). In other words, blast is then very survivable!
(3). Simply allow nuclear radiation doses in modern cities to be attenuated severely by a factor of about 100 (from the 2011 Los Alamos report unobstructed desert "free field" initial nuclear radiation dose data study for the shadowing by intervening the buildings of in New York City) - before you include the actual shielding by a building people are in, which is much better for INR than Glasstone claims, because essentially ALL of the urban area outdoor 100-fold reduced radiation dose is SCATTERED, not direct, so it is energy-degraded and not the highest-energy direct gamma and neutrons (which are attenuated severely on the transit through all the buildings in the radial line from the bomb)! Putting in "/100" to the computer formulae is not rocket-science! Simple. Nothing in the universe is perfect, but this correction is easy, and gives a minimal baseline for realism for the urban effects of nuclear weapons, lacking in all anti-nuclear diatribes. For higher yield weapons, the increased ranges for given radiation doses will lead to increased attenuation, since at increased ranges there will be more concrete buildings intervening in the the radial line from fireball to target, and although scattered radiation builds up at greater distances, it has lower energy than unscattered radiation and therefore is less penetrating (easier to shield). The most penetrating and wide-angle scattered nuclear radiation dose is from neutrons, but for the full range of 13 different nuclear weapon designs in the 1984 EM-1, the effective mean free-path for the surface burst neutron dose over the distance 1-2 km only ranges from 189 to 221 metres (the latter being weapon type 13, the neutron bomb). (The neutron dose will essentially completely arrived - except for a small portion due to delayed neutrons from fission products like bromine-90 - before blast damage occurs to those buildings lcated near the crater.) Glasstone is widely ignored when pointing out in one table in the last chapter - contrary to many free-field charts and graphs - that 50% survival in modern concrete buildings in Hiroshima occurred at 0.12 mile for the 16 kt air burst at 600 m; this scales up by the cube-root scaling law to predict 50% survival at 1.2 miles from a 16 megaton air burst at 6 km altitude; initial radiation dose distances scale as a weaker function of yield than blast.
Additionally, the blast effects data (relating say overpressure to casualties) is way off in left-wing anti-nuclear propaganda. The actual Hiroshima and Nagasaki data proves much greater survival than bogus theoretical assessments: in reality, 100% people are not nude standing behind windows facing the blast while wearing roller-skates to ensure they are frictionlessly blown straight out of the 42nd floor by a 3psi blast, and killed by the impact from the gravitational fall to the pavement 420 feet below. Instead of the 1979 US Office of technology assessment claim that 50% of people are killed at 5psi, in Hiroshima and Nagasaki more than twice this was needed for the same effect, even without effective duck and cover or taking shelter (CLICK HERE FOR REPORT CONTAINING THE EVIDENCE FOR THIS). Although blast duration increases with yield, this has no effect if the pressure is below the threshold for damage, so Glasstone's curves are wrong for not reverting to cube-root scaling at high yields (impulse rules at low yields, peak pressures rule at high yields; Glasstone ignores this transition in his nonographs for building damage, which is corrected by by the secret EM-1; report Dirkwood Corp report DC-P-1060 found that the blast mortality effect was 50% at 32 psi peak overpressure in modern non-seismic concrete buildings in Hiroshima, or 17 psi for 1 megaton, without duck-and-cover to reduce exposure to flying glass, debris and blast wind drag; contrasted to 5 psi in anti-nuclear disarmament propaganda lies).
For the correct application of Hiroshima's lessons to modern higher yield nuclear war threats from Russia, see for instance the 1970s congressional testimony of T. K. Jones of Boeing Corporation in hearings linked HERE (February-March 1976 congressional Civil Defense Review), and HERE (November 1976 Nuclear War Survival hearings). Whenever the factual evidence surfaces, it is falsely labelled "controversial" or "wrong" by lying mainstream media charlatans, fraudsters, and bigoted snake oil salesmen, and ignored for political left-wing propaganda purposes, or the "arms controllers" simply tell lies claiming falsely that civil defense is a joke, just as they did in the 1930s (when civilian gas masks were discounted as a simple solution to deter Hitler from dropping his gas bombs on cities for a knockout blow!) and 1970s, debunked by T. K. Jones' famous 1979 letter to congress, extract below, which led to his being appointed Deputy Under Secretary of Defense for Strategic and Theater Nuclear Forces on June 1, 1981 under the new Reagan Administration, which aimed to win the Cold War by science and technology, not lose freedom via Russian nuclear coercion. Note that while the ACDA - i.e. the U.S. Arms Control and Disarmament Agency, whose faked nuclear weapons/war effects calculations lay behind the disastrous 1970s nuclear parity SALT farce which now results in dictators again intimidating democracies as was the case in the 1930s due to disarmament scams for "peace" which led to WWII - claimed 50% of people are killed at 5 psi peak overpressure from a megaton, while in fact U.S. classified Defense Nuclear Agency research showed that Russian public shelters were built to take 150 psi i.e. surviving within the 0.83 mile fireball radius of a 5 megaton surface burst, Russian apartment basement shelters were built to survive 60 psi, and good Russian improvised expedient shelters built outside cities survived 40 psi in American blast tests and gave upwards of 200 fallout protection factor (i.e., reducing the maximum hotspots of 20,000 rads to a survivable 100 rads and averting casualties).
ACDA disarmament bigots simply lied in the traditional "H. G. Wells" 1930s-sci-fi-style of disarmament fantasy, in testimony to congress, about the motivation and the detailed work of those people who disproved them, they ignored the classified data on blast and fallout shielding in their "effects" models, or their calculations assumed that people failed to use fallout shelters in order to deceptively "reduce" fallout protection factors by a factor of 7, by simply assuming people would go outside to be exposed to unshielded fallout (like most people, they also massively exaggerated the mean gamma ray energy of fallout during the sheltering period, as we have previously exposed, which is debunked by the measurements after the Redwing Zuni and Tewa tests) - they also lied that Jones didn't include fallout casualties when in fact he did include fallout correctly, finding that you don't get fallout casualties with the high degree of radiation shielding in shelters, an exact analogy to the situation where the 100,000 protection factor of activated charcoal gas mask filters gave no gas casualties in 1938 research, and disarmament bigots tried to claim that was some kind of ignorant dismissal of the horrors of true gas war so they would "arbitrarily" assume that only say 50% of people put on gas masks in order to then falsely claim that gas masks were somehow "calculated" to only work for 50% of people - i.e. only those assumed to be actually wearing them! - a travesty and abuse of scientific modelling (like lying that you have done detailed calculations proving that car seat belts make no difference in accidents, when in fact you have merely assumed that nobody wears the seat belts!), when in fact the true excellence of gas mask protection was proved to successfully deter Hitler from using gas on civilians with gas masks, saving millions contrary to the hate attacks on civil defence by disarmament propaganda deceivers (who recognised that civil defence made deterrence credible, and so was a threat to their bigoted plans for peace at any price):
ABOVE: extracts from the famous 1979 T. K. Jones Boeing Corporation letter, page 2, debunking "arms control" nuclear weapons effects liars in detail. This really exasperated my dad, John B. Cook, who was a Civil Defence Corps instructor in the 1950s, but was old enough to live through the 1930s appeasement era when Philip Noel-Baker repeated lied on the effects of gas bombs, claiming gas masks will never work, because babies and the elderly won't put them on properly, blah, blah, so we must ban evil civil defence and instead guarantee peace by appeasing the Nazis because of we don't, they will DEFINITELY gas us all with a massive gas bomb raid on day 1 of war. In fact, Philip Noel-Baker did this first in a BBC radio speech in 1927, 6 years before Hitler was elected. Family members who knew the truth from gas attacks in WWII - largely negated by simple gas masks and going into shelters for droplets of persistent liquids like mustard agent - had to put up with this lying BBC and other media propaganda for disarmament throughout the 1930s, to the joy of the Nazis who were secretly rearming and preparing for invasions (not necessarily war, since Hitler would have been quite happy to "peacefully" invade the world and then use efficient gas chambers to dispose of those whose race or views he found to be "offensive", like modern snowflakes today). What really irritated dad, however, was that Philip Noel-Baker, having lied about gas effects in his February 1927 BBC radio broadcast and throughout the 1930s to great applause from pacifists who effectively did Hitler's bidding, was made a Lord and a Nobel Peace prize winner for appeasement propaganda lies that led to world war, and then did the same thing all over again during the cold war, issuing nuclear weapons lies. In a 1980 House of Lords debate on Civil Defence, he lied that the air burst in Hiroshima produced lethal fallout: "It covers everything in Hiroshima not already rendered lethal, and so those who have escaped the flash, the blast, the fire, will die within a short time. The first atomic bomb weighed two kilograms. It was little larger than a cricket ball. ... In 1978, more than 2,000 died in Hiroshima from its long-term effects."
Every word here is totally untrue, and easily disproved, but nobody in the House of Lords explained the facts to him, so this he quotes on page 5 of his 1980 Ecology Party book "How to Survive the Nuclear Age", and on page 6 he adds an attack on civil defence: "I feel the same outrage in 1980 when the Home Office [UK Government civil defence] propose to circulate a a copy of a pamphlet entitled Protect and Survive to every citizen. ... To strengthen the walls and ceilings as the pamphlet suggests, he needed a garden, a spade, sandbags, and the strength to dig and transport a ton of earth." However, the infirm or elderly don't need to hire an army of helpers to make a fallout shelter, because - contrary to Philip Noel-Baker - you can simply use water from a hose to fill up water filled bags inside boxes which do the shielding, as explained in the Home Office scientific advisory branch Fission Fragments magazine article (reprinted in the Royal Observer Corps Journal, vol. 27, issue 2, February 1985, page 26, below). In any case, in actual implementation, you would have some organization for civil defence in time of crisis, with people in nighbourhoods helping one another (lending hose pipes, helping to assemble emergency shelters around tables in homes, etc). Noel-Baker ends his case by absurdly calling for disarmament as a "sure way to avoid the war", by again ignoring the lessons of his own 1930s disarmament war effects propaganda which led to appeasement and thus the encouragement of enemy aggression, triggering the Second World War: "This is not a utopian dream. It is the system by which David Lloyd George disarmed Germany in 1919..." This claim typifies Noel-Baker's absurd, self-contradictory nonsense, since DLG's 1919 "system" led to another, far worse, world war, not to peace.
In that 1980 Ecology Party book "How to Survive the nuclear age", there is after the deceptions from Labour Party Lord Noel-Baker, a summary of civil defence shelter advice, but then the book ends with the transcript of the final big speech from Lord Mountbatten to the arms control anti-nuclear propaganda institute SIPRI at Strasbourg on 11 May 1979 (the IRA tragically ended his appeasement campaign with a bomb on his boat off the coast of Sligo, Ireland, on 27 August 1979): "A military confrontation between the nuclear powers could entail the horrifying risk of nuclear warfare [hardly likely if we have overwhelming superiority for credible deterrence, as we should have had - but did not have - in the 1930s to deter Hitler]. ... A new world war can hardly fail to involve the all-out use of nuclear weapons [this is debunked by former NATO General Sir John Hackett's book "The Third World War" which shows how escalation risks will be controlled even in the event of a Russian first-strike on Britain, provided that we are prepared for nuclear war - this book will be discussed in detail later in this blog post, below]. ... Let us all resolve to take all possible practical steps to ensure that we do not, through our own folly, go over the edge."
ABOVE: the most advanced and latest American "counterforce" nuclear weapons, the oralloy (Oak Ridge Alloy, aka U235 loaded secondary stage) W88 nuclear warheads were designed to knock out the huge well shock-insulated Russian SS-18 missile silos when they had a physical vulnerability number of 52L7, corresponding to a peak overpressure of 7000 psi, which is well within the crater radius. This is highly relevant today, since ehe SS-18 (in Russian nomenclature: R-36M2) is still in service (like the American W88), and the Russians have 46 of them, each with 10 warheads of 800 kilotons each, i.e. a total of 10x46 = 460 nuclear warheads and 3680 megatons. These 211 ton SS-18s are due to be replaced with the latest 208 ton Sarmat (RS-28) missiles (which made its first test flight on 20 April 2022, during the Ukraine war), extending the range from 11,000 km for the SS-18 to 18,000 km for the Sarmat. Unfortunately, as this declassified report shows, as with the Russian civil defense shelters, the silo hardness was underrated and the physical vulnerability is not 52L7 as originally supposed. The SS-18 silos could take much higher peak overpressures than 7000 psi and related ground shock, cratering throwout, etc. (The current "best guess" - and this is not proof tested due to the ban on atmospheric nuclear testing - is that it takes a peak overpressure of 10,000 psi to blow the silo door off the SS-18 silo and wreck the missile, which occurs at a distance from the warhead similar to its inertial gyroscopic CEP targetting error if the accurate GPS satellite navigation system is taken out by high altitude bursts, so to get a high kill probability you need to target many warheads per silo, a hugely inefficient strategy when all the enemy has to do is launch the SS-18 out of the silo before your warheads arrive!) In addition to this underestimate of the hardness of vital military "counterforce" targets in Russia, the Americans also massively over-estimated the cratering and ground shock effects for high yields in ordinary soils (not easily broken coral reefs!). (For references, please see the earlier blog posts about cratering exaggerations linked here and here.) The points we want people to take away, or at least openly investigate and question are:
(1) countervalue (anti-city) effects of nuclear weapons are bunk because, aside from the mistakes and deliberate omissions Glasstone and Dolan made for propaganda purposes in their 1977 edition, if the chips really do go down, you or your opponent can simply evacuate cities - most of which self-evacuate at 5pm every weekday, anyhow - evacuation is not a miracle, despite what Scientific American or Bulletin of Atomic Scientists says - before issuing an ultimatum, just as the UK did with evacuating kids from London in Operation Pied Piper on 1 September 1939 before issuing an ultimatum and then declaring war 48 hours later,
(2) you or your opponent can not only safeguard the civilians in cities by evacuating them (or putting the people into shelters/basements etc if you have them, as the Russians do, and as thankfully the Ukrainians do which is a key reason they have been able to fight the Russian invasion, as a result of having previously been part of the civil defense obsessed USSR), but 100% of missiles in silos can also be safeguarded from destruction by simply firing them out of their silos, if seriously threatened by a counterforce (anti-silo) enemy attack. In other words, if you decide to credibly target enemy nuclear weapons (a very costly strategy in terms of the number of W88 warheads per silo for any significant chance of damaging a >7000psi peak overpressure-requiring SS-18 missile silo, which are about as well protected as the concrete and steel around most nuclear power reactor cores), your targetting policy will encourage the enemy to launch first, to save their missiles from being taken out! So using nuclear weapons to target other nuclear weapons in hardened silos (or hidden in the sea in submarines!), apart from being extremely inefficient and costly in terms of your stockpile, is also a policy that provokes the risk of enemy "launch on warning" crisis instability because you are, if "successful", removing the enemy's protected second strike retaliation capability, and once the second strike option is gone, they are pushed back into the old first-strike aka launch-on-warning policy, which is extremely dangerous if their radar operators mistake some third party's missile testing for a launch against them, etc., etc. So the obsessive "disarmament fantasy" of only using nuclear weapons to try to deter other nuclear weapons in silos by targeting them, is a dangerous illusion that provokes crisis instability and risks an accidental nuclear war, in addition to being an exceptionally ineffective deterrent! All you do with that delusion is to deter the enemy from a second-strike policy, and force the enemy into a dangerous first-strike/launch on warning policy! If you can knock out the enemy warheads in their silos, the enemy will simply ensure that there is a very high probability that their missiles have been launched out of their silos before your warheads arrive, so you will be uselessly destroying EMPTY missiles silos! (your warheads take 25 minutes to arrive for an ICBM between continents, and 10 minutes for a back door attack of an SLBM launched from a submarine; less time is required for a Russian sub to hit NY or LA because they are beside oceans, unlike Moscow and most Russian targets that are well inland!).
(3) In any case, how do you target enemy SLBMs in submarines hidden at sea? Similarly, the most numerous Russian ICBM in their stockpile is the mobile SS-27 Mod 2/RS-24, of which they have 135 missiles on 16-wheeled mobile launch vehicles which can move around, with 4 separate MIRV nuclear megaton warheads per missile and a range of 11,000 km. How do you target them as they move around during a crisis situation? They can easily move position enough to survive an nuclear warhead in the US stockpile during the 25 minutes while your missiles are on the way to hit them in a crisis situation, so you are literally trying to hit a moving target - do you really believe America will be able to reprogram the target locations for ICBM warheads in flight as they are moving? The whole idea would be amusing if it wasn't so tragic (there was an effort to create a warhead which could track its moving target and adjust its trajectory accordingly, the MARV - Maneuverable Reentry Vehicle - the only known Western MARV was the Pershing II warhead, which disarmed as part of the INF treaty to appease Russia/pro-disarmament politicians in the West). So the whole idea of using nuclear weapons to hit enemy nuclear weapons before they are launched is crazy and dangerous. It's no joke that all the disarmament propaganda claims falsely that nuclear weapons have only the purpose of targetting other nuclear weapons in silos. That policy is dangerous, because it just encourages the enemy to get the weapons out of their silos before your weapons can arrive, so you are not deterring the enemy to launch their weapons, but forcing them to launch on warning, a lunatic policy! Nuclear weapons are only effective in a counterforce operation against armies on the move, either as a deterrent or to physically stop invasions without collateral damage by air burst enhanced neutron weapons. The only real use of nuclear weapons should be, as Oppenheimer said, as a tactical threat to stop the military invasions and attacks that triggered two world wars.
Nuclear weapons are exceptionally good at deterring (or stopping) armies on the move! Not so if they are dispersed in defensive positions like hasty earth covered emergency civil defense shelters that resist 40 psi peak overpressure and give a protection factor of 200 or more against radiation; but the point is that they deter enemy military offensives and once the enemy has crossed your border you are within your rights to stop them; the credible threat will prevent invasions this way, ending world war. (Nuclear weapons are also effective at destroying enemy nuclear weapons in flight, e.g. the 2 kt W66 neutron warhead in the American Sprint ABM missile could melt down the fissile material in Russian nuclear warheads in flight in the atmosphere, and the 5 Mt W71 x-ray warhead of the Spartan ABM missile would ablate, deflect and destroy Russian warheads in space; they also knock down trees to create demilitarised zones in jungle warfare which enable easy identification of insurgents entering those zones for attacks.)
ABOVE: Russian nuclear weaponeer Boris Vasilyevich Litvinov explaining how the world's smallest diameter nuclear artillery shell and allegedly cleanest thermonuclear weapon work to President Putin on 30 March 2000, during his visit to VNIITF at Snezhinsk, Russia. (President Putin wrote on his filmed entry on the Visitor's Book at VNIITF Snezhinsk - screen print of the entry is included later below in Russian - "The biggest danger facing Russia and the whole world is the violation of the balance of power at the cost of huge efforts and sacrifices to the Soviet. The Union managed to achieve a balance of great merit in this, due to your team together. We are obliged not only to maintain the existing achievements but also to achieve new frontiers relying on the talent and courage of our scientists. With hope and love, Vladimir Vladimirovich, March 31, 2000". This is from the film the lab put out in 2005, and we include a selection of stills from it. We're not as yet entirely sure of the reason for the possible discrepancy in dates of Putin's visit, 30 and 31 March 2000, from different sources. It is obviously possible Putin stayed overnight, arriving on 30 March 2000, and signed the visitor's book when leaving the next day.
Peace through credible war deterrence:
The worthless Budapest Memorandum on Security Assurances signed by Russia, UK and Ukraine on 5 December 1994 led the way to the removal of the war-preventing nuclear deterrent from Ukraine: the liars claimed like the 1930s Nazis that signatures on paper would guarantee survival, not deterrence. OK, you edit a TV show or paper, and you think this is not relevant to today's problems faced by the person in the street unless Putin actually presses the button. You're a liar if you claim this. Paying higher energy prices? It's due to nuclear disarmament liars allowing Putin to start the war, cutting energy supplies to Europe, driving up prices. Like the disarmament of the UK up to 1935 (and slower rearmament thereafter, to avoid provoking a tantrum from Nazis, in the name of "peaceful coexistence" with state terrorism and racism), Ukraine's nuclear disarmament from 1994-8 guaranteed war, not peace; it gave the green card to the supporter of enemy disarmament, Russia. Nazis in the 1930s pushed for Western disarmament in the name of "peaceful" gas chamber genocide and "peaceful" invasions without opposition (because their enemies had disarmed), just as the thugs do today. As you'll see below in this post, this is not "news". It's the regular, repeating, trick used by bankrupt dictatorships to start world wars: get your enemies to disarm then invade neighbours with impunity! They don't think they can be ever "proved lying evil warmongers by humble yours truly" because they will just keep parroting the lie that if Ukraine had nuclear weapons, there would have been a nuclear war between Ukraine-Russia, not peace: HEY GUYS COUNTRIES WITH NUCLEAR WEAPONS HAVEN'T HAD NUCLEAR WARS YET! HISTORY SHOWS THE ONLY COUNTRY TO HAVE BEEN ATTACKED WITH NUCLEAR WEAPONS (AUGUST 1945) DID N-O-T HAVE ANY NUCLEAR WEAPONS. BEING NUCLEAR UNARMED DIDN'T SAVE IT FROM BEING NUKED. OK NOW? NO?????????! LET'S SEE ALL THE SECRET FACTS THAT THE "SECRECY-OPPOSED" BLOGGERS REFUSE TO TELL YOU IN THE NAME OF THEIR EFFORTS TO START A NUCLEAR WAR:
ABOVE: from 1992-8, Russia pushed for Ukraine (which has excellent nuclear competence, having Europe's largest nuclear power station, which could have been used to irradiate lithium to produce tritium for independent maintenance of nuclear warheads), to disarm its extensive nuclear warheads using its Cold War traditional Russian supported hypocritical "peace through nuclear disarmament" propaganda movements in the Western media and Western politics (including the current US president) and in 1994 signed a peace guarantee to protect Ukraine's borders, with the UK and USA. Many of us were worried that this was a recipe for a future world war should Russia's attempt at reform fail, leading to a decision to rebuild the USSR starting with the biggest component outside Russia, i.e. Ukraine. At the same time, Boris Yeltsin and the Russian nuclear labs were producing a new generation of tactical nuclear weapons to counter and cancel US conventional weapons, according to a secret-classified 2000 CIA report (linked here). "During Putin's mobilization announcement, he[Putin] also threatened to use nuclear weapons in Ukraine, baselessly accused Western countries of provoking him with "nuclear blackmail," and said his remarks weren't a bluff. Russia has the world's largest nuclear arsenal, equipped with both tactical nuclear weapons as well as strategic nuclear weapons, which would be used against cities. "Russians that I keep in touch within Russia are convinced he's going to go nuclear," [ex-CIA agent] Baer told CNN. "I don't know how well-connected they are, but this threat — it was a threat initially — but the more trouble he's in, the more likely he's going to use nuclear weapons"." - Business Insider, 27 September 2022, Ex-CIA officer says Putin is 'completely cornered' and the chances of his using tactical nuclear weapons in Ukraine are increasing 'by the day'. "The US and its allies would eradicate Russia’s military troops in Ukraine and sink its Black Sea fleet if Vladimir Putin uses nuclear weapons, said former CIA director David Petraeus." - US would destroy Russia’s entire army if Putin use nukes in Ukraine, says former CIA director, The Independent, 3 October 2022. Nobody believes Petraeus because Putin has already made clear he will start start off with a Fourth Protocol style false-flag (contrived) nuclear attack on a Russian supply dump or whatever in Ukraine, pretend that is an enemy attack, and use that as a basis to "retaliate" using nuclear weapons. This is actually a very old diplomatic "fog of war" tactic, which President Kennedy's brother Robert referred to as "sinking the Maine again", in a taped discussion on 16 October 1962, when he considered it during the Cuban Missiles Crisis as a possible false-flag "justification" for invading Cuba to remove those Russian nuclear weapons. (The USS Maine was sunk, supposedly by a Cuban mine, in Havana Harbor on February 15, 1898, and was used to "justify" the American war with Spain in April.) As a pretext for war, this doesn't matter a dime from the perspective of whether the West believes it. It's just about creating an iota of doubt to enable it to violate agreements. Similarly, Russia has never admitted the lethal attacks with Po-210 (UK, 2006) or Novichok (UK, 2018). It's not about whether the West believes any of it. It's purely about Russian bureaucracy. The more evil there is, the more fake justification. (The Nazis were also obsessed with generating fake justifications by diplomatic bureaucracy to excuse genocide and invasions; this always seems to be about trying to go down in history as holier-than-holy.)
ABOVE: useful entry about Babaev's design work on Russian thermonuclear weapons in the 2005 Russian book, Герои атомного проекта (Heroes of the atomic project), with side by side Russian and English text translation (since this is important to establish as hard fact beyond any doubt, for the record): "In 1961-1962, Yuri Nikolaevich (Babaev) and his colleagues developed new, more advanced charges. Most of these charges are still in service with the Russian Army. For his participation in the development of a number of thermonuclear charges with high specific characteristics, Yu. N. Babayev was awarded the title of Hero of Socialist Labor in 1962 with the award of the Order of Lenin... Under the leadership of Yu. N. Babayev, new nuclear and thermonuclear charges of various values were developed in subsequent years to equip most branches of the Armed forces of the USSR. ... The further direction of Yu. N. Babayav's work was the radical improvement of nuclear charges - a dual approach. ... Such thermonuclear charges were simpler in design and manufacturing technology.". (Tip: to translate Russian to English from a low quality image scan, upscale the image of the text with Zyro, and then translate the result using Yandex translate.)
ABOVE: the precise nature of Putin's nuclear threat, photos from both the Russian nuclear weapons labs museums (older stuff is in Sarov, but the latest Russian very small MIRV warheads whose shapes reveal design data are in the RFNC-VNIITF Museum at Snezhinsk including the pink painted warheads which are not in the Sarov collection). The first two-stage 1.6 megaton yield Russian thermonuclear weapon, tested in 1955, RDS-37, had a spherical secondary (fusion) stage which required isotropic compression (unlike early American cylindrical designs). The Russian design omitted the plastic foam used to fill the radiation channels in the early UK two stage warheads (and modern W87 and W88 etc.) to deliver x-rays isotropically to the secondary stage. Instead, the Russian design used precise geometric mirroring of x-rays by a large (1.5m diameter) ellipsoidal (prolate spheroid) shaped case, with the fission primary at one focus and the secondary stage at the other (legendary Russian thermonuclear warhead designer Yuri Trutnev has confirmed this use of a lead lined case, a reasonably effective x-ray mirror - it isn't a perfect mirror since the "reflection" is accompanied by a lot of absorption of radiation - in the RDS-37 and later designs, with low-density material merely used as an x-ray absorber as a surface covering on the spherical secondary charge and not as a radiation channel filler - as discussed later in this post, below). This design - without plastic foam filling the radiation channel - was first used by America a year later, as the Egg device tested during Operation Redwing shot Huron (discussed and illustrated later in this post). It has its advantages: faster and more efficient compression with less risk of neutron pre-initiation of fissile materials in the secondary stage, since x-rays are slowed down by plastic foam, but travel faster than neutrons if simply reflected from the case. Therefore, when using the outer case as an x-ray radiation mirror, the speed of delivery of the x-rays to the secondary (to compress it) is faster than the speed that neutrons can arrive, so you don't need a neutron interstage barrier the way you do for devices employing a plastic foam filling, which slows down the x-rays delivery time and allows more neutron fission in the secondary to occur before full compression by x-rays.
Anything large in the case which creates x-ray "shadow" zones increases anisotropy of x-ray delivery to the secondary stage. This problem doesn't exist for the early American cylindrical stages, where the compression geometry is simply axial symmetry, i.e. radial compression in 2, not 3 dimensions. (To double the density of the secondary, radial compression of a cylinder requires a 29.3% reduction in radius, compared to just a 20.6% reduction of radius for spherical compression to achieve similar doubling of density.) But this outer case x-ray mirroring also has the disadvantage that the overall diameter of the outer radiation reflecting case must be large in comparison to the diameter of the spherical secondary charge (at least several times larger), or you do not get a sufficiently isotropic compression of the secondary stage (i.e. similar compression from all directions), because if the case is too small, the finite size of the secondary stage itself blocks reflected radiation from hitting it on the opposite side to that in proximity to the primary stage, which reduces compression, efficiency, and yield. This is just a simple shadowing problem that you can see in a room lit by daylight from a window. If you place a large object in front of the window, it creates a shadow behind it, so it is not isotropically illuminated (i.e. lit equally on all sides). If you place a smaller object in front of the window rather than a huge object, this shadowing problem is reduced or even eliminated because enough light can get into the room around the object, to be reflected back on the far side of that object by the walls of the room - particularly if you have mirrors on the walls - since the mirrors can then reflect light back so that the object is illuminated more uniformly on all sides (isotropic exposure, as opposed to anisotropic - unequal - exposure of all sides; for a diagram illustrating a suppressed example of the effects of a certain kind of fascinating anisotropic radiation exposure, please - for example - see my very brief 1-page long PDF paper linked here!).
ABOVE: illustration of the problem of the anisotropic x-ray exposure of the secondary stage and some of its possible solutions, namely fill the case with foam to slow down and diffuse the x-rays to a uniform concentration everywhere in the case (a terrible idea for several reasons, e.g. it reduces recoil ablative impulse, allows neutrons time to arrive and pre-detonate any fissile material in the secondary stage, and it means the outer case has to hold the whole thing together for longer while the fusion burn hopefully starts, but this is nevertheless still used in Western devices), make the case huge so you can reflect x-rays more uniformly on to the far end (right ride above) of the secondary stage, use two primaries - one on each side of the secondary stage - as Russia does still, or design an "interstage" shield to go between the two stages above to try to even-up the exposure on each side of the secondary stage (but be careful to design it well, or you will over-shield the secondary and it won't get compressed at all!). The 1958-tested double primary Russian solution has the genius that easy to design: you don't need to bother to make careful design calculations at all!
ABOVE: two versions of the RDS-37 first Russian nuclear weapons design. The first shows RDS-37 as the simple prolate spheroid elliptical system for x-ray mirroring, fitted into an RDS-6 case as shown on a globalsecurity.org page (the RDS-6 case was used for the earlier 1953 400 kt Alarm Clock externally boosted device). Actual film from the 22 November 1955 test of RDS-37 show a longer bomb, probably with an added parachute to slow the bomb down while the delivery aircraft escapes (the 1953 RDS-6 test, unlike RDS-37 in 1955, didn't need a parachute, as it was a near surface burst). The second illustration is from a Russian language source (Military Russia, Бомба с зарядом РДС-37) showing a slightly different variation in which there is a very clever concave shield used between primary and secondary stages to try to achieve uniform (isotropic) irradiation of the spherical secondary stage with x-rays. The source given is not a declassified report but a Russian youtube video. The problem is that this convoluted design, while simple to draw, is very complicated to design in terms of calculating the sizes and shapes of the various elements for optimum performance, requiring 2- or 3-d simulations by computers unavailable at the time, even in America. It is more likely to be the basis of the 500kt two-stage single primary devices developed in 1958 and used in the 50mt Tsar Bomba (discussed and illustrated later) than the first 1955 test of a two-stage device. The diffulties with the isotropic compression of spherical devices was a key reason why early American bombs had cylindrical secondaries with just radial compression not isotropic compression; they are far more straightforward for design calculations, because you don't have to worry about how to get radiation to the far side of a sphere! In other words, you don't need 3-d calculations. The simpler prolate spheroid case, with primary and secondaries at the two elliptical focii, is easier to analyze mathematically without a computer using straightforward geometrical considerations (cf. Winterberg's 1981 book Physical principles of thermonuclear explosive devices, Fig. 4 on page 28 and discussion of x-ray mirrors on page 32, as shown later in this post), and thus more likely what was tested in 1955. This is because there is less to go wrong, and it is easier therefore to get a definite result if the design has an error; whereas, if you test a design with lots of innovations, and it fails, you learn nothing because you don't know which of the many factors caused the failure (it is not even the case that you know that one thing has gone wrong, which can be discovered by elimination after many changes and tests, because there could be several different design failure causes all working together, in a radical product with lots of innovation!). The same youtuber also has a video of the design of the 50Mt Tsar bomba which is also incorrect, showing a more modern device with a single primary stage (completely debunked below in this post, since that 50mt bomb was provably set off by two 500 kt thermonuclear charges). In both designs above, the overall bomb case diameter is at least three times the diameter of the secondary charge, which is necessary to prevent an x-ray shadow on the side of the secondary furthest from the primary stage, resulting in anisotropic compression.
ABOVE: cartoon-style (non-blueprint) sketch of the problems of designing the interstage to stop neutrons from the primary stage from pre-detonating and deforming the fissile U235 (oralloy) in the secondary stage, while x-rays are diffusing (relatively slowly, compared to x-rays in a vacuum) through the foam shown in blue, to allow isotropic compression of the secondary stage. This requires detailed 3-d computer simulations and nuclear tests for verification, and is very difficult design engineering to get right. Traditionally, the light weight interstage has been beryllium, a toxic brittle material, for its transparency to x-rays and opaqueness to neutrons, while not being excessively heavy for a missile payload. There has been a recent effort to replace the toxic, brittle beryllium interstages with safer, more durable interstages made of alternatives like boron, cadmium and lithium. (For aircraft delivery, where weight is less crucial than for missile warheads, U238 can be used as the neutron shield. But if weight is not an issue, you could simply have a clean secondary stage, comprising of Li6D and lead or tungsten pusher, without any fissile material, so then you don't need a neutron shield interstage!) But the more fissile oralloy there is in the secondary stage of a W88 warhead, the closer it is to criticality, so the greater the complexity of the design to keep primary stage neutrons from predetonating it, while still allowing sufficient channelling of x-rays. This is a complex design trade-off to get right, requiring sometimes multiple nuclear tests and re-designs, which explains why detailed data is still classified secret. (Not shown in the sketch is a thick neutron shield cylinder enclosing the entire secondary stage to reduce its vulnerability to predetonation by neutrons from defensive nuclear warheads from the Russian ABM system. When such a U238 neutron shield shell is shown in diagrams, it is usually misinterpreted as some sort of tamper or reflector to help the reaction! In addition, the primary and secondary stages are simplified. Fissile material would have a hollow core supplied with D+T boost gas from an external flask, prior to detonation. There is also the external x-box with capacitors that must be charged up with HV from a battery powered inverter prior to detonation, supplying large parallel current pulses to detonators and neutron initiator tubes. These are also safety features, helping to ensure that several stages of preparation must be undertaken in order to achieve a full-yield detonation, so the weapon is relatively safe in an accidental fire or impact.)
One of the biggest secrets of thermonuclear weapons became clear from the "clean" H-bomb research at Operation Redwing in 1956; the Zuni (15% fission, 3.53mt total yield) and Tewa (87% fission, 5.01mt total yield) were basically identical designs, but U238 in the Tewa device was replaced with lead in Zuni, and Zuni was topped up with extra li6d to try to compensate. As the results showed, although fusion is on paper more efficient than fission, in reality it was not possible in that design to get as much yield out of the cleaner device. In other words, in the dirty design, the fusion stage is just used as an external boosting tool to release high energy neutrons to fission U238, which produces most of the yield. An exception to this is the more efficient pusherless pulse-shaped isentropic compression system tested in the Ripple II device in 1962, discussed later, where it is claimed by its designer Nickolls that a higher efficiency of thermonuclear burn was achieved than in pusher devices (this isn't reflected in the overall yield/mass ratio of the entire device, which was just a prototype; we're talking just about the yield/mass ratio of the fusion capsule in Ripple II, not the entire prototype bomb whose mass is not relevant to a final warhead system).
"To form the direction of energy transfer, at the suggestion of A. D. Sakharov, the [1.6mt RDS-37] primary and secondary modules were enclosed in a single shell, which had a good quality for reflecting X-rays, and measures were provided inside the charge to facilitate the transfer of X-rays in the right direction. Yu. A. Trutnev in the course of this work proposed a method for concentrating the energy of X-ray radiation in material pressure [a low density x-ray absorbing layer around the secondary stage, discussed later in this post with quotations from Trutnev himself about it], which made it possible to effectively carry out radiation implosion. During this development, he also proposed a method that determined the predictability of the configuration of channels for the transfer of x-rays, which later found wide application in two-stage thermonuclear charges. ... In this case, the problem of ensuring spherically symmetric compression of the secondary module was radically solved, since the time of “symmetrization” of energy around the secondary module was much shorter than the compression time of this module. ... The fact is that the overall mass parameters of the RDS-37 charge and the first samples of thermonuclear charges of the USSR that followed it and the first thermonuclear charges of the USA are fundamentally different. The characteristic value of the ratio of length to diameter of the first thermonuclear charges of the USSR is less than 2, and for the first thermonuclear charges of the USA it is 3.2–4.8.This difference indicates fundamental differences in the structure of the secondary modules of the first thermonuclear charges of the USSR and the USA. The thermonuclear charge modules of the USA had a cylindrical configuration, while the thermonuclear charge modules of the USSR had a spherical configuration." - I. A. Andryushin, A. K. Chernyshev, and Yu. A. Yudin, Creation of the first samples of thermonuclear weapons, http://wsyachina.narod.ru/history/coretaming_5.html (deleted site, but available now on Wayback Machine at https://web.archive.org/web/20130515010737/http://wsyachina.narod.ru/history/coretaming_5.html).
In the sense the Russians I. A. Andryushin, A. K. Chernyshev, and Yu. A. Yudin (above quotation) argue, that America first tested thermonuclear weapons with cylindrical "pipe" secondaries whereas Russia was straight-in with the spherical secondaries now used in compact MIRV warheads, Russia seems to have been ahead in the 50s. The Russian design of 1955 was essentially duplicated by the American Egg design (Redwing-Huron) of 1956. But it was bulky because to get isotropic compression efficiently of a sphere using radiation mirroring from the inside of a prolate spheroid reflecting case, the case needs to be at least 3-5 times the diameter of the secondary stage (unlike getting isotropic compression from plastic foam, where you just need a few cm wide radiation channel!). So Russia wasn't ahead, unlike Britain which in 1957-8 successfully used spherical secondaries (like Russia), but with plastic foam in the radiation channel (unlike Russia) to make the secondary stage compression isotropic while reducing the outer case size to a minimum. If you just use the outer case as a mirror (as the Russians Ya. B. Zel’dovich, Yu. A. Trutnev, and A. D. Sakharov did very successfully with their 1.5m diameter RDS-37 in 1955, and the Americans did with their Egg device in the Redwing-Huron test of 1956), and don't instead use foam to fill the case to absorb and re-radiate x-rays isotropically, you will always need a REALLY HUGE DIAMETER outer bomb case for the geometry to work efficiently! This is due to the immutable mathematical laws of geometry. So although they were able to use a single primary stage with success in 1955, they had a huge problem with trying to miniaturise that design without going back to fission bomb yields.
There were only three possible ways to change their design to get their huge 1955 H-bomb small enough physically to fit into the warhead of an ICBM: (1) change the shape of the secondary to the simpler to compress geometry of a cylinder, where you ignite the end closest to the primary stage and then an auto-catalytic self-burning wave is hopefully initiated (as used in the early 1952 American Ivy-Mike test), but the Russians had already investigated and discarded Teller's original Superbomb "pipe" (the Russian word for it); (2) fill the radiation channel with plastic foam to make the energy delivery isotropic to the secondary, but this is less efficient since the x-rays are delivered more slowly than by simple case reflection (through having to be repeatedly absorbed and re-radiated in a mathematical "drunkard's walk" going in all directions by the electrons in the foam), and this x-ray energy delivery delay also allows neutrons to arrive and partly melt down, expand and pre-detonate any fissile materials in the secondary stage (unless you have an efficient neutron shield or interstage between the primary and secondary stage, which is hard to design effectively without good electronic computers, which the Russians then lacked); or finally (3) use linear-implosion of the final fusion stage, by using TWO primary stages, one on each side of the fusion stage, within a cylindrical casing, wired in a simple parallel circuit for simultaneous detonation. Linear implosion is never the most efficient solution, but it is necessary to get a very small diameter thermonuclear weapon for a ICBM warhead. So it turns out that the Russians use a very different approach to compact nuclear warheads than America and Britain. Yuri Trutnev in 2017 explained the details (this has now been deleted from the Russian site):
"... Avraamy Zavenyagin ... said - take a thermonuclear charge, surround it with atomic charges, blow them up at the same time, they will squeeze it. ... This idea was later developed by our theorist Viktor Davidenko. In fact, he proposed a scheme for the so-called two-stage charge - a casing in which there were spatially separated atomic and thermonuclear units. The explosion energy of the primary atomic stage would be used to ignite thermonuclear reactions in the secondary stage. Our outstanding specialists Yakov Zel'dovich and Andrei Sakharov had great hopes for this scheme of so-called nuclear implosion. ... I did a lot of work on the theory of the efficiency of atomic charges. I knew that when they explode, a lot of energy comes out in the form of x-rays. And I began to think about how to make it so that the thermonuclear charge is overlaid with a light substance - "coating", these can be chemical elements with a low number, having very good thermal conductivity, and with the help of X-ray radiation from the explosion of the primary atomic charge "coating" heat up. At the same time, its substance would evaporate outward, towards the radiation, and as a result, as during the movement of a rocket, a reactive impulse would be created, directed into the secondary charge and creating the pressure necessary for effective compression of the thermonuclear "fuel". But how was it possible to ensure a uniform, symmetrical effect of radiation on the spherical surface of a thermonuclear charge with a "coating"? Here I am stuck. ... Zel'dovich proposed exactly how to direct X-rays, Sakharov showed that this radiation is not absorbed by the walls of the casing, but remains in it, and therefore a uniform effect on the surface of the thermonuclear unit can occur. And my idea is a "coating" of a light substance to transfer radiation to the required pressure. ... I already had another idea in my head - a more advanced product based on a new principle for designing a thermonuclear charge. After testing the RDS-37, the next day in the evening I called my friend and colleague Yuri Nikolaevich Babaev to the bank of the Irtysh and said: "Yura, let's try to do just such a thing." And he agreed. We returned to Sarov and drew a charge diagram and proposed it. This product received an index of 49. I will not say what it is. Product 49 is similar to the RDS-37, but not in everything. They started laughing at us, this is all nonsense, nothing will work out for you. In short, they didn’t support us because they didn’t understand. ... We were supported by Igor Vasilyevich Kurchatov. The test of product 49 took place on the Day of the Soviet Army, February 23, 1958 at the test site on Novaya Zemlya. The success was very big. In 1958, several tests of products of different capacities based on the 49th charge took place. He went into a series, he was put on rockets, and this was already the basis of our country's thermonuclear weapons. ... I said to Khariton: "Yuli Borisovich, let's make a 100-megaton charge. Maybe then the West will understand that it would be pointless for them to increase their megatonnage further." He agreed. But here, for safety reasons, we also made a half-power charge, replacing the uranium-238 stage with lead. ... The Americans understood that they would not frighten us, but we would frighten them. And they lowered the power in their trials. We could have done more, but what's the point?" - Yuri Trutnev, The creation of nuclear weapons is a special kind of creativity, ria.ru/20171122/1509304656 22 November 2017 (this page has now been deleted, but is available on Wayback Machine at https://web.archive.org/web/20220429180233/https://ria.ru/20171122/1509304656.html)
To get small thermonuclear warheads for missiles, after successfully testing a compact linear implosion primary stage for nuclear artillery (detailed later in this post), at the suggestion of Yuri Trutnev, starting in 1958, the Russians began testing thermonuclear weapons having two compact primary stages, one on each side of a spherical or cylindrical thermonuclear charge, wired in parallel electrical circuit using large krytron vacuum tube switches to get simultaneous detonations and a more uniform compression of the secondary stage. This was because they lacked the computers America and Britain used to design smaller thermonuclear warheads where plastic foam was employed to deliver x-ray energy uniformly to a secondary charge from a single primary stage. Trutnev suggested replacing the two primary stages with two 500 kt thermonuclear weapons to achieve a 50 megaton clean test in 1961. But what is more important is that this whole approach was continued by Russia with more practical weapons, under the leadership of Yuri Nikolaevich Babaev (1928-86):
The use of two primary stages (or two whole thermonuclear devices, for higher yields) to compress a fusion capsule inside a narrow tube casing without plastic foam to make the radiation isotropic is like a linear implosion system for fusion charges: the central (main) fusion charge will be most compressed along the axis of the bomb than from the sides, so it can be elongated so that it becomes a sphere when compressed (below). This is avoided in US and UK weapons by the use of computer designed low density baffles of plastic foam to make the x-ray energy isotropically compress the secondary (the foam doesn't do the compression, the x-ray ablation of the secondary does it; the foam is merely used in modern Western designs to reduce anistropic compression of the secondary, missed out by the Russian approach which uses two primary stages or two thermonuclear stages for larger devices, instead).
"The A6027 charge was tested on October 30, 1961 at the Novaya Zemlya test site. ... The creation of nuclear weapons by the Soviet Union, despite the hardships of the post-war period, has become an effective factor in deterring any aggressors from launching new global wars [the aggressor is Russia, fighting democracies in Georgia, Crimea, Syria and Ukraine, eh]. ... The young theoretical physicist Yu.A. Trutnev proposed the idea of creating a 100 Mt superbomb, which could frighten foreign skeptics who believed that Soviet nuclear scientists were significantly weaker than American ones [subservience and slavery to authority is always a weakness compared to free thinking trial-and-error based innovation for profit and to supply customers with the latest products they want and need; the backwardness of Russia in microelectronics for decades illustrates the failure of centralised control most clearly; free countries also have this problem but the people are generally better capable of overcoming the tyranny]. The idea was supported by Academicians A.D. Sakharov, Yu.B. Khariton and Ya.B. Zeldovich. The top leadership of the country, having agreed on the issue with scientists, decided to create and test super-powerful weapons. The final decision to resume nuclear testing and create a superbomb was made in July 1961, when the scientific leadership of KB-11 (VNIIEF) reported to N.S. Khrushchev on the possibility of developing a hydrogen bomb with a capacity of 100 million tons of TNT. ... [Copying the USA, which opened a second nuclear weapons lab, Lawrence Livermore, to challenge its first lab at Los Alamos...] In 1955, by decision of the Government, a second nuclear center was established - NII-1011 (RFNC-VNIITF) in Chelyabinsk-70 (now the city of Snezhinsk), where a third of the employees of KB-11 were transferred. ... After the adoption of the decree of the Government of the USSR on the resumption of testing of nuclear weapons in July 1961, KB-11 began emergency work on the development, theoretical justification and preparation for testing not only superbombs, but also a series of other nuclear weapons. Even before this decision, the theoretical physicists of KB-11 were distributed to develop "their" charges. Therefore, to develop a superbomb, it was decided to call Dr. Ph.D. Adamsky V.B., by connecting to it a theoretical physicist - a recent graduate of MEPhI Yu.N. Smirnov, as well as the initiators of the creation of the superbomb, Ph.D. Trutneva Yu.A. [center of photo below, in front of bomb] and Ph.D. Babaeva Yu.N. Academician Sakharov A.D. took over the development leadership. ...
"The situation was aggravated by the tight deadlines for the start of tests (09/01/1961), the lack of a computer park to carry out the proper number of calculations. I had to use all the computers of the Mathematical Institute of the USSR Academy of Sciences (mathematicians at KB-11 worked there at night and on weekends). And only on October 24 (6 days before the tests) was the final report on the design of the bomb and the theoretical justification completed. But even then A.D. Sakharov (already without a computer) additionally worked out the necessary improvements. A large number of serious innovations were applied in the design of the superbomb itself and its charge. A powerful thermonuclear charge was made according to the “bifilar” scheme: for radiation implosion of the main thermonuclear unit, two thermonuclear charges were placed on both sides (front and back) to ensure synchronous (with a time difference of no more than 0.1 μs) ignition of thermonuclear “fuel”. KB-25 (VNIIA) finalized a serial detonation automation unit for this charge. It seemed to A.D. Sakharov that the calculations carried out on a computer were not enough. 2 days before the product was sent to the test site at 8 pm, Sakharov came to the workshop, approached the product (the body of the bomb was open and access to the charge was provided from both sides). Andrei Dmitrievich looked inside, felt the construction, then sat down on a chair in the corner ... the academician drew a sketch, where it was proposed to install lead belts 60 mm thick from the side of the initiating charges on the inner conical surface of the charge body. I call the director of KB-11 B.G. Muzrukov at one in the morning: “What should I do, after 36 hours, sending?” Answer: "Do as Sakharov said!" At 6.00 in the morning, the designers draw “squirrels” in the shop and after 4 hours the lead belts are ready (from the memoirs of the head of the assembly shop of the KB-11 plant A.G. Ovsyannikov). After 40 years, when, on the instructions of the director and first deputy scientific director of VNIIEF, Academician of the Russian Academy of Sciences Ilkaev R.I. In the most powerful computer center in Russia, VNIIEF, the calculations for the three-dimensional problem "Mimosa" were checked, it was confirmed that the absence of these lead belts would lead to a significant distortion of the radiation implosion sphere and a decrease in the explosion power by ~ 80%. So the thought of the academician turned out to be much more perfect than computers available at that time. ... In the history of Russia, a certain pattern was noticed in the creation of hypertrophied samples of unique products: the Tsar Bell (which did not ring), the Tsar Cannon (which did not shoot) and, finally, the Tsar Bomba (which was blown up with some excess of the calculated power - 52.5 Mt). ... only about 2 percent of the energy of the explosion came from the fission reaction, the rest of the energy from the fusion reaction ... The creation and testing of the most powerful thermonuclear charge in the world with a capacity of 50 Mt served as an impetus for reducing the arms race throughout the world. And this is the great merit of our outstanding nuclear scientists. [In plainer words, Russia succeeded in starting the West on the road from nuclear superiority to arms control parity, allowing the dictatorship to survive longer before going bankrupt.]" - A.V. Veselovsky, honorary veteran of the RFNC-VNIIEF, head of the scientific and testing department (in 1956-2009), laureate of the USSR State Prize, http://www.proatom.ru/modules.php?name=News&file=article&sid=3364
"After the end of the moratorium in 1961, they returned to the task of creating a superbomb, but now it was a thermonuclear charge with an energy release of 100 Mt, which was to be placed in an aerial bomb developed according to the “202 project”. At this stage, the development of a new super-powerful charge was carried out in KB-11 on the initiative of Yu. A. Trutnev and A. D. Sakharova, the team of authors also included Yu. N. Babaev, V. B. Adamsky and Yu. N. Smirnov. Original solutions and accumulated experience made it possible to implement this development extremely quickly, and the charge was successfully tested on October 30, 1961. Among the features of this charge, it should be noted that the large volume of the charge (due to its high energy release), required significant amounts of X-ray energy for implosion. The developed nuclear charges did not satisfy this condition, and therefore, a previously developed two-stage thermonuclear charge with a relatively low energy release [~500kt] was used as the primary source of the “superpowerful charge” [TWO of them, one on each end of the main fusion stage!]. This [~500kt] charge was previously developed by Yu. A. Trutnev and Yu. N. Babaev. ... In 1962 Yu. A. Trutnev and V.S. Lebedev developed a smaller version of the superbomb with an energy release 2.5 times less than the 1961 version. The reduction in energy release and overall mass parameters made it possible to count on equipping a heavy ICBM with such a charge. The charge was tested in a non-full-scale version using passive materials [lead ablator/pusher and case lining] that significantly reduced (as in the 1961 test) the release of radioactivity in the test explosion." - I. A. Andryushin, A. K. Chernyshev, and Yu. A. Yudin, Development of the nuclear weapons program of the USSR, http://wsyachina.narod.ru/history/coretaming_6.html (deleted page but it is still available on Internet Archive Wayback Machine here: https://web.archive.org/web/20130921043813/http://wsyachina.narod.ru/history/coretaming_6.html).
"The development of super-powerful thermonuclear charges was considered as an important task for both nuclear institutes of the USSR. The developments of nuclear charges discussed above, tested on October 30, 1961 and September 27, 1962, were carried out at VNIIEF (Arzamas-16 [now called Sarov]). As examples of the development of super-powerful charges carried out by VNIITF (Chelyabinsk-70) , one can cite devices tested on September 25 and December 24, 1962. In the first case, a charge was tested that was close in characteristics to the VNIIEF charge tested on September 27, 1962. The comparison shows that they were essentially duplicate designs. In the experiment on December 24, 1962, a super-powerful charge with a nominal energy release of about 50 Mt was tested under conditions of a non-full-scale explosion with a power reduced by about half. The test confirmed the expected characteristics of the charge. Note that in the test version, which is a high purity charge, the actual nuclear [fission and fallout] energy release was small. ... The first test for the same purposes [reduced fission yield proportion, i.e. cleaner] was carried out in the USSR on October 20, 1958 at the test site on Novaya Zemlya in a modification [lead replacing U238] of the previously tested "dirty" two-stage charge. The level of nuclear [fission and fallout] energy release achieved in the development was an insignificant part of the total energy, however, the total [fusion plus fission] energy release was significantly reduced compared to the base [U238 containing] charge. ... Already in 1954, it was realized that a non-nuclear explosion of a nuclear charge is accompanied by the dispersion of plutonium, which is part of it, with its subsequent fallout. The first experiment in which practical results were obtained in this regard took place on October 19, 1954, when an unforeseen failure of a nuclear charge occurred. ... The first experiment to study the "single-point safety" of a nuclear charge was carried out in the USSR on August 26, 1957, and, in essence, the USSR nuclear test program in the interests of security began to be implemented in 1961. A total of 11 experiments of this type were carried out during the period of atmospheric testing in the USSR. After the transition to underground nuclear tests, 14 more special nuclear tests were conducted for these purposes, as well as an additional 17 experiments as part of group nuclear explosions. ... The maximum nuclear energy release in the nuclear safety experiments was realized in the experiment on September 9, 1961. This value is close to the maximum energy release realized in the US nuclear safety tests during the period of atmospheric tests, which is 500 tons of TNT equivalent. [Nice to know Russia is concerned for nuclear safety!]" - Nuclear testing and the creation of nuclear weapons, http://wsyachina.narod.ru/history/nuclear_testing_1.html (deleted but still available on Wayback Machine: https://web.archive.org/web/20130515005510/http://wsyachina.narod.ru/history/nuclear_testing_1.htmlABOVE: physicist and author Colin Bruce Sibley's 1977 book Surviving Doomsday, which was reviewed by Peter Laurie in New Scientist, 13 April 1978, p97, where Laurie points out: "I'm afraid that Mr Sibley has fallen into the popular error of confusing what modern weapons can do, with what they will do." This followed his 1976 Foreign Affairs Research Institute paper, "The strategic significance of Soviet civil defence preparedness". Unfortunately, Sibley had been producing children's educational stuff, for example producing a vinyl record of the 1969 Moon Landings, Journey to the Moon (Pickwick International Ltd.), and in 1976 he authored The How and Why Wonder Book of Energy and Power Sources and The How and Why Wonder Book of Oil (Transworld Publishers Ltd., 1976 and 1979), see illustration below. He used this same children's book style to write Surviving Doomsday! Sibley (1935-2008) later edited Protect and Survive Monthly. The reason for this was the attitude of publishers: they knew that hard facts on nuclear weapons didn't sell easily and needed a lot of "gloss" to be economically viable for printing. This same farce occurred with a UK Government booklet, Protect and Survive.
ABOVE: Air raid sirens operator Yoshie Oka who survived the nuclear explosion near ground zero in the military bunker just north of Hiroshima Castle on 6 August 1945, identified the B29 bombers (which Tokyo had tracked by the Enola Gay B29 bomber radio call sign), and passed on a report to her seniors in time to get the people of Hiroshima into their air raid shelters, most of which survived intact against a 16 kt nuclear air burst at 600 metres altitude (by cube-root scaling, similar peak pressures would occur at ground zero for a 16 megaton burst at 6000 metres altitude, since the cube-root of a 1000 fold increase is 10, i.e. 10^3 = 1000, and although the blast duration is also 10 times longer, the blast arrival time also scales up similarly, so it also takes 10 times longer for the blast wave to arrive at ground zero, giving people a far better chance to "duck and cover", and of course in the higher yield burst the scaling of the bomb case thickness and burst altitude will allow far more mean free paths of radiation shielding metal and air which make the initial radiation a minor threat like the thermal flash inside concrete buildings). But the army officers in Hiroshima were taking breakfast so there was a long delay, and eventually at 8:13, just two minutes before detonation, she finally received the order to start the complex sequence needed to sound the public air raid sirens, putting codes into the air raid sirens to permit operation! She was still trying to get the air raid alarm out when the bomb went off. This is why there was no warning in Hiroshima and most people were not in the plentiful public shelters or concrete buildings. Shamefully this vital evidence for the failure of civil defense in Hiroshima is completely edited out of the fake news which passes for nuclear weapons information in so-called free democracies.
ABOVE: Peter Laurie's article on civil defence in the Sunday Times Magazine, 10 December 1967, pages 39 et seq., formed the basis of his later book Beneath the City Streets. The article states (on page 50) that the popularist (faked) megadeath nuclear war casualty figures were even in 1967 not without precedent since exactly the same media trash exaggerations on casualties and knock-out blow strategy also existed before WWII (contributing to the appeasement that encouraged Hitler): "a very similar situation existed in 1938. Everyone believed - and these were official estimates - that the Luftwaffe could flatten half London in 3 weeks and kill 3,000,000 people. Few Londoners ran away, and few got bloodthirsty. More to the point, a booklet was issued to every household that winter: The protection of your home against air raids. In August 1939 Mass Observation did a survey on what people knew of something simple: the two air raid sirens. Five out of six got them wrong ..." Laurie's article was, of course, published just 4 months before the British civil defence corps was abolished by hard left wing Prime Minister Harold Wilson in March 1968. But Laurie points out on page 40 of his article that the London underground (ordinary tube trains, not just the specially hardened shelters at 8 stations) will survive directly below a 5 megaton burst at 8,000 feet altitude, which optimises blast effects on buildings, and he points out that the "fireball does not touch the ground: there is no significant fallout." Sure, you can reduce the height of burst to try to damage underground facilities and to cause fallout, but then you no longer optimise the effects on ordinary houses. Laurie in his massive nuclear weapons effects diagram on the same page points out that 75% of British houses are demolished at 5.25 miles from the 5 megaton air burst at 8,000 ft altitude: "but 90% of people under stairs will live" (the WWII Morrison table shelter principle, which is independent of bomb yield because the weight of a collapsing house is independent of bomb yield). His article states that the 1967 British civil defence budget was 10s per person, compared to 17s 6d in West Germany, but adds that "Since 1948, when [nuclear war] civil defence began, we have spent over £1000 million; roughly the capital cost of the deterrent and delivery systems." Laurie also points out in his 1967 article that the very high protection factors of deep shelters make them unfeasible because Russia can produce rockets to negate them for 33% of the cost of the shelters. In order to win an arms race by economic attrition through civil defence, therefore, you need cheaper shelters that cost less than the weapons the enemy is making to try to break through your defences (the same point occurred in WWII, when cheap indoor Morrison table shelters were deployed instead of the economically-crippling gold-plated variety, having been invented and tested by Lord Baker and his assistant Edward Leader-Williams, who - with Frank H. Pavry and George R. Stanbury - in the 1950s tested key British WWII shelters against nuclear weapons at Monte Bello and Maralinga and used the results to develop them into effective but cheap nuclear shelters, published finally in the 1982 UK Government book Domestic Nuclear Shelters - Technical Guidance). Finally, Laurie makes the point that devastation in war can transform politics into dictatorial communism: "Russia, for example, by the end of the first world war [the Red revolution was in October 1917 in Russia] had lost, in comparison to 1913: one half to two thirds livestock, one half grain production, 90% of coal, steel, textiles, and transport, 28 million people." The lesson is that if your country is devastated by the effects of war like Russia or Germany in 1918 or Vietnam in 1975, the survivors are likely to have to live in a politically extreme dictatorship, justified by the sheer destruction and the populist need for revenge at any cost.
ABOVE: photos of paranoid dictatorial Russia from the 25 March 1933 Illustrated London News article, when British citizens in Moscow (Allan Monkhouse, John Cushny, W. H. Thornton, W. H. McDonald, Charles Nordwall et al.) were arrested by the OGPU of Stalin's regime on trumped up charges of sabotage (they all worked for the British Metropolitan-Vickers electrical engineering company, and the Russians claimed falsely the company was planning to blow up the Dnieprostroy Dam by pouring sand or acid into the turbines, when in fact the blades were 5 tons and were washed clean by millions of gallons of water daily!), and when ordinary Russians had to endure food rationing in peacetime.
ABOVE: the relationship of civil defence by a dictatorship to its aggressive policy (such as Germany's compulsory cellar bunker shelters in the 30s and Russia's in the cold war) was documented in the 14 October 1933 Illustrated London News showing civil defence anti-disarmament propaganda in Hitlers Nazi Germany, stating: "In view of the world-wide interest in the question of disarmament, with which is involved that of the re-armament claimed by Germany, it is significant that the Nazi regime appeas to be conducting all its activities, and training of the youth of the nation, on more or less military lines ... We illustrate in the photographs on these pages one phase of the all-pervading propaganda calculated to create in the German people the fear that one day or another they may be attached ... children are taught to take refuge promptly in special underground shelters and to extinguish, by sand, fires of the kind that might be caused by bombs. The spirit in which these lectures are given may be gathered from the following extract ... : " 'Germany is not allowed to have fighting aeroplanes on land or sea.' Thus runs Clause 198 of the shameful Treaty of Versailles ... Germany has been completely disarmed and has no defence against an enemy air attack." Having first set up effective German civil defence in 1933, the next step of the Nazis was to re-arm in preparation to setting the clock back to 1914. Stalin did the same in Russia. Putin follows suite. As Herman Kahn forecast over 60 years ago, we are now paying the price for neglecting civil defence and also for refusing to put freedom loving states ahead in the arms race. The options available to such weak loons are disastrous.
ABOVE: Western nuclear disarmament from 31,255 US warheads in 1966 to 3,750 in 2020, is a repeat of the weapons effects exaggerations for disarmament propaganda, a lying disaster which allowed a defeated Germany in 1918 to rearm and start WWII, as these quotations from an earlier blog post here prove, which also quotes Kissinger (before he was corrupted by political expediency) explaining how tactical nuclear weapons can safely be used to deter invasions: ‘The Hungarian revolution of October and November 1956 demonstrated the difficulty faced even by a vastly superior army in attempting to dominate hostile territory. The [Soviet Union] Red Army finally had to concentrate twenty-two divisions in order to crush a practically unarmed population. ... The high casualty estimates for nuclear war are based on the assumption that the most suitable targets are ... cities ... The elimination of area targets will place an upper limit on the size of weapons it will be profitable to use. Since fall-out becomes a serious problem [i.e. fallout contaminated areas which are so large that thousands of people would need to evacuate or shelter indoors for up to two weeks] only in the range of explosive power of 500 kilotons and above, it could be proposed that no weapon larger than 500 kilotons will be employed unless the enemy uses it first. Concurrently, the United States could take advantage of a new development which significantly reduces fall-out by eliminating the last stage of the fission-fusion-fission process.’ - Dr Henry Kissinger, Nuclear Weapons and Foreign Policy, Harper, New York, 1957, pp. 180-3, 228-9.
TIPS: There is compendium debunking commonplace anti-nuclear CND disarmament propaganda, exaggerations and fake news on nuclear weapons effects and deterrent capabilities linked here. Also, each post on this blog can be viewed in either a simple format, e.g. for this current post, https://glasstone.blogspot.com/2022/02/analogy-of-1938-munich-crisis-and.html is the simple (faster loading) format, or you can view it (slower loading) in a fancy format by adding: ?m=1 to the end of the URL, e.g. https://glasstone.blogspot.com/2022/02/analogy-of-1938-munich-crisis-and.html?m=1
NATO needs to come to its senses and rearm to deter WWIII instead of stupidly leaving Putin with more nuclear weapons than anyone else, to intimidate like Hitler (see 1930s newspapers below, which spell out the problem plainly). The problem is, the media is dominated by nuclear liars just as it was dominated by gas war liars in the 1930s, who encouraged war while pretending to be doing the opposite. Fighting a conventional war using Ukraine as proxy, while having an inferior nuclear stockpile, is hardly credible nuclear deterrence (please click here for our brief declassified data debunking Glasstone's lying data on nuclear weapons effects) . Also see the compendium linked here for more detail on the actual declassified effects found in Hiroshima, contrary to Glasstone's very deceptive treatment. Please also click here for our declassified 4069-pages compendium of nuclear weapons deterrence data, debunking the Ukraine's "security through nuclear disarmament" myth YEARS AGO!
ABOVE: "During the Cold War, it was often assumed that the use of nonstrategic nuclear weapons would eventually escalate to East-West strategic nuclear exchanges (Quinlivan and Oliker, 2011, p. 72). ... there seems to be a recognition within Russia of brinkmanship hazards—namely, that Russian nuclear use could get out of hand and result in further escalation (Quinlivan and Oliker, 2011, p. 72)." - Anthony Barrett, 2016 RAND Corp report RAND-PE-191-TSF, False Alarms, True Dangers? - Current and Future Risks of Inadvertent U.S.-Russian Nuclear War, page 7.
ABOVE: W54 Davy Crockett tactical nuclear deterrent of approximately 0.02kt yield and 20ft burst altitude, tested in front of Robert Kennedy, Attorney General, in the final Nevada atmospheric nuclear weapon trials to deter invasions: 2,100 were deployed in the 1960s, successfully deterring a Russian invasion. But ALL tactical nuclear weapons were removed in the 90s after false propaganda from appeasers, leaving a dangerous gap in the spectrum of deterrence. (Photo credits: US National Archives photos above taken on 14 July 1962 show tactical 0.02kt+/-10% yield W54 Davy Cockett nuclear weapon projective M388 on M29 launcher at Nevada Test Range, with two soldiers from the Heavy Weapons Platoon, 1st Battalion, 12th Infantry, 4th Infantry Division, US Army.) The Ukraine invasion is an invasion deliberately caused by the Budapest Memorandum on Security Assurances signed on 5 Dec 1994 to remove the nuclear deterrent from Ukraine to prevent war. Like the disarmament of the UK up to 1935 to guarantee "peace in our time", loads of excuses are used to try to justify weakness and enemy aggression, by left wing warmongers who profit by causing war with its refugee crises with financial and humanitarian disasters. Until the so-called peacemakers disarmed Ukraine of its 176 intercontinental ballistic missile (ICBM) launchers with some 1,240 warheads, leaving Ukraine to make improvised Molotov cocktail petrol bombs (polystyrene dissolved in petrol in a bottle) to try to protect its kids from Russia, Russia was deterred from invading Ukraine by reliable nuclear deterrence. Ukraine had experts and still does have expertise on servicing and using those nuclear weapons - in evidence, before they were invaded, we bought the confidential Russian nuclear weapons employment manuals (LINKED HERE) from the Ukrainian military on ebay. In fact, Russian nuclear weapons are more straightforward and easier to service and employ than American nuclear weapons, so the lie that the Ukrainian nuclear weapons in 1994 couldn't be serviced by Ukraine - which has Europe's largest nuclear reactor and all the nuclear expertise that goes with it - is just that, a lie by anti-nuclear folk.
As the illustrations below from Dr Shelton's Reflections of Nuclear Weaponeer, a shelter well within the fireball radius of the first multimegaton hydrogen bomb survived 330 psi peak overpressure, and a 1.4 megaton W49 thermonuclear warhead detonated at 400 km altitude above Johnston Island as the Starfish prime test on 9 July 1962 produced EMP effects 800 miles away in Hawaii (colour photos on the front page of the 9 July 1962 Honolulu Star Bulletin, mentioning that streetlights were turned off and air raid sirens were activated - due to EMP). The Russians later, on 22 October 1962, performed such an EMP demonstration with a 300 kt warhead detonated at 290 km altude, so they could use this type of "nuclear weapon demonstration" threat as an alternative to usual disarmament propaganda about nuclear weapons automatically being used to kill people by Hiroshima-type low altitude air or surface bursts:
ABOVE: in the Cold War, Russia was deterred from invasions using a variety of tactical nuclear weapons including 2,100 W54 Davy Crockett tactical nuclear weapons, and later - after the Russian invasion of Afghanistan began - 550 deployed W79 thermonuclear 1.1 kt W79 neutron bombs (to achieve a significant fusion yield with the very brief compressions available with a sub-kiloton fission yield, a second stage capsule of tritium and deuterium gas had to be employed, instead of the solid lithium-6 deuteride secondary stages that require neutron fission of the lithium-6 to produce tritium, prior to fusion; the x-ray compression at such a low yield was too brief to allow the fission stage neutrons to arrive at the secondary stage in time to fission enough lithium-6 prior to the x-ray compression pulse). The fission primary stage of the W79 shell uses small-diameter linear implosion system invented for a variety of purposes, both nuclear and non-nuclear, by US Government explosives expert Bernard Drimmer, and has now been declassified and published (after decades of being kept secret) as US Patent US5450794A/en, presented without the central fissile core for compression, as merely a method to increase to a maximum the efficiency of underwater explosives (just sticking a detonator into a lump of explosive leads to incomplete burning since some of the explosive ends up being blasted outwards into cold water before detonating; using the implosion system with the burning wave going inwards therefore maximises efficiency for non-nuclar torpedoes). The W79 deterred both massed troop invasions and also tank and APC invasions, since 14.1 MeV D+T fusion reaction neutrons penetrate armour very efficiently (even without the removable fusion capsules, the neutrons and gamma rays from 0.8 kt pure fission yield of the W79 was still a highly effective deterrent against Russian tanks; the fusion capsule reportedly added 0.3 kt of fusion yield, 80% of this or over 0.2 kt in the form of 14.1 MeV neutrons). Click for a Secret (now declassified) Los Alamos report detailing why we need the W79 enhanced neutron tactical nuclear weapons to deter Russian expansionism (report LA-12063-MS "The Future of Non-Strategic Nuclear Forces: Are These Capabilities Still Needed," dated 1991, LINKED HERE), and linked here with a previous slightly different declassified version linked here (which gives the names of the LA-12063-MS report authors, unlike the OpenNet version), ignored by left wing (discussed on previous blog post linked here - a brief extract from this 74-pages long report, containing detailed evidence that tactical nuclear weapons kept the peace in the Cold War much to the fury of Russia, is shown below; notice that tactical nuclear weapons are asymmetric in that they are more useful to deter invasions than to cause invasions, hence they are a stabilizing influence in crisis instability despite left wing propaganda to the contrary):
"Denying an aggressor force the use of massed formations of armor is the single most important aspect of the W79."
LA-9004 then goes on to suggest a lower yield version of the W79 for use against individual tanks, like the Kennedy era portable 0.02 kt W54 that could be fired by individual soldiers, air burst at 15 metres altitude to eliminate local fallout, blast and heat collateral damage. Page 5:
"Tank crews within 25 m of the weapon would be immediately incapacitated. Civilian populations 300 m from the point of detonation would be completely safe. ... Beyond 300 m, exposed personnel might be temporarily blinded from looking directly at the detonation, but would suffer no burns to exposed skin. ... The effect of blast on civilian structures near the battlefield would be trivial. Three hundred metres from the point of detonation windows would rattle but not break. ... the fallout would be expected to be confined to the battlefield itself. ... The principal advantage of such a device in reducing collateral damage from local fallout is that it simply does not produce much in the way of fission fragments or activated weapon debris."
LA-9004 then points out, on pages 7-8, that such a defensive low yield weapon with no significant risk of collateral damage is of no significant use to terrorists, contrasted to easy-to-procure alternatives.
ABOVE: the 405-pages, originally Secret 1969 Proceedings of the Tactical Nuclear Weapons Symposium, Los Alamos document LA-4350-MS, has been declassified and is available on Opennet (pdf is LINKED HERE). For 1 kiloton of D-T fusion air burst at 750 feet altitude (for the W79 this fusion yield is reportedly 0.3 kt, so you multiply the following doses by 0.3, before adding on the fission dose from 0.8 kt of fission), Dr Hudson's Lawrence Radiation weapons lab article "Clean nuclear explosive research applicable to tactical nuclear weapons (Secret-RD)", applying clean fusion tests research to peace-making deterrent purpose in the 1969 conference LA-4350-MS, shows that the unshielded dose at a 1,000 ft ground radius or range (i.e., distance from ground zero, not the slant distance from bomb) is 800,000 R (85% being neutrons), falling to 100,000 R at 2,000 feet (75% being high energy neutrons, with the rest being high energy gamma rays from inelastic neutron scattering by the air), and 10,000 R at 3,000 ft radius, but a relatively trivial 10 R at 7,000 ft radius, preventing collateral damage to nearby civilians. The U.S. Defense Nuclear Agency assessed that immediate permanent incapacitation for all tasks occurs at 18,000 R, or 8,000 R for physically demanding tasks, while 3,000 R produces immediate temporary incapacitation. The original 1972 secret Capabilities of Nuclear Weapons DNA-EM-1 gives initial radiation data for 8 designs of nuclear warhead, but it was revised and expanded to 13 designs in the 1984 edition. However, the neutron outputs from three of these are practically identical: nuclear warhead types 4 and 7 (1-30 kt boosted two-point implosion and 1-10 kt multipoint implosion) and 11 (30-300 kt cleaner tactical nuclear warhead), all giving about 83.6 rads per kiloton at 1 km ground range for a surface burst on unobstructed silicate soil in sea level density air, plus about 28 rads/kt of secondary gamma rays (the fission product initial radiation dose is independent of bomb design details apart from fission yield and total yield, being 19.3, 332 and 13,000 rads for 100% fission total yields of 1, 10 and 100 kt). For comparison, nuclear warhead type 13 in EM-1, the 1-2 kt enhanced neutron warhead produces about 20 times that dose (1,660 rads/kt of neutrons and 450 rads/kt of air secondary gamma if surface burst; a 1 kt "type 13" neutron bomb air burst at 500 m altitude gives a dose at ground zero of 170,000 rads of neutrons plus 27,200 rads of secondary gamma rays, according to EM-1). At the other end of the scale, the lowest neutron dose, just 0.666 rads, is produced by the type 10 in EM-1 (the low-yield fission primary stage "dial a yield" option of a B61 thick-cased thermonuclear weapon having multiple yield options). This is because the outer casing on a weapon with high yield options absorbs most of the neutrons from the primary stage, and thereby shows that you cannot simply use the low-yield option on a B61 as a replacement for tactical nuclear weapons like neutron bombs.
Note that once NATO C3I command is neutralised by Russian nuclear forces, e.g. EMP high altitude burst effects if not blast and nuclear radiation from surface or low altitude bursts, blitzkrieg by troops protected by armour enables rapid invasions, even in fallout radiation areas (tanks and APCs offer good shielding against the low energy gamma rays from fallout, unlike the higher energy initial flash of gamma rays and neutrons). When on 8 December 1991, the presidents of Russia, Belarus, and Ukraine dissolved the USSR, the Soviet military was 3.7 million strong. "From 1945 to 1948, the Soviet Armed Forces were reduced from about 11.3 million to about 2.8 million men", while the Soviet Union actually increased in size, as puppet governments were installed across half of Europe, despite the American nuclear weapons monopoly until 1949. Today, with the tactical nuclear deterrent removed from Europe, it is only necessary to blow up the military and political bases in Europe to destroy its capacity to harm Russia by economic warfare and military support to enemies of Russia. A business which puts its rivals out of operation becomes a monopoly. It doesn't necessarily have to send in huge numbers of "boots on the ground" to physically occupy all the destroyed rival business offices in order to succeed in "winning" the war; remember that in both the Third Reich and USSR/Warsaw Pact/Iron Curtain era, occupied countries were put under puppet governments (Vichy France, etc.) in a thinly camouflaged effort to portray the occupation as a mutually cooperative "peace initiative" (i.e., "you will do was we say, then we won't shoot you and blow your cities up, how's that for peacekeeping collaboration?").
To give some idea of the complexity (the diagrams above are open-source, unclassified, not to scale, and demonstrating principal concepts pictorially rather than as design blueprints) of the compact 1950s designs of tactical warheads that now form the primary stages in American two-stage missile warheads, please see the biography of John S. Foster, Jr., the Lawrence Livermore National Laboratory physicist who led the designs of the compact primary stages needed for compact SLBM and MIRVed ICBM warheads. The quotations about the history of the modern primary designs that follow are from T. F. Ramos, Call Me Johnny, Lawrence Livermore National Laboratory, report LLNL-BOOK-783447, 2019:
"Much of the effort to design an atomic device relied on using a computer program, or code, to guide the designers. The group’s computer code support came from Bob LeLevier and Chuck Leith. Leith was a real computer pioneer. He had written out the Laboratory’s first codes on one of the world’s first computers, the UNIVAC. The physicist Jim Wilson, who was a distinguished graduate from UC Berkeley and a member of T Division, was yet another code developer, and became Johnny’s technical leader. In 1954, in a series of nuclear tests called Operation Castle, the Laboratory had once again fielded a shot that failed. This was a test of a Megaton Group secondary. It was the third successive nuclear test failure of the Laboratory. There were powerful men in Washington, DC who wanted to see the new Laboratory in Livermore shut down. The stress of the failure had its effects on Lawrence and Teller, and they both suffered from attacks of colitis and had to be hospitalized. Herb York came down with Valley Fever and had to remain at home in bed rest. That meant that the future of the nuclear weapons program at the Laboratory rested squarely on the shoulders of Johnny Foster and Harold Brown. ...
"Johnny was especially interested in designing a weapon for the Army, which during the Korean War, had experienced massive “human wave” attacks of Chinese soldiers – assaults that had almost destroyed Eighth Army. The Chinese Army attacked with large, closely packed formations that overwhelmed American defenses. Chastened, the Army wanted a nuclear artillery shell that would deter any nation from using those tactics again on a battlefield. ... He did not know it, but a team of Los Alamos engineers and technicians had developed a diagnostic technique called a pin dome that could measure how a device imploded. ... The Cleo was a tactical weapon, suitable for the Army, and it promised to be one of the smallest atomic devices yet developed. The Cleo concept required multidimensional modeling to fully understand its workings, and Jim Wilson performed Cleo calculations on new codes that he wrote. But even with Wilson’s talents, multidimensional computer codes were primitive affairs in 1954. ... For its transport to the Nevada Test Site, the Cleo was constructed in two parts, and each part was placed into a reinforced Samsonite suitcase [Cleo was tested in Nevada on 1 March 1955 as 7 kt Teapot-Tesla, atop a 300 ft tower. The predicted yield was 3.5-7kt. It was only 10 inches wide, 39.5 inches long, 785 lb, and used an external Zipper neutron gun. An even smaller version, Cleo II, was tested as 2 kt Teapot-Post on 9 April 1955, 34.2" long, weight 322 lb]. ... The Cleo had worked; the first warhead from the Laboratory to do so. Someone, apparently, had leaked information out about how the device had been delivered to the tower. Time magazine wrote a story about a new type of nuclear weapon that could fit inside a suitcase. ... Lawrence opened a discussion by asking, “Why do we need small diameter nuclear weapons?” Teller responded that they were needed for nuclear artillery, which had been identified as a need for the Army."
- T. F. Ramos, "Call Me Johnny", Lawrence Livermore National Laboratory, report LLNL-BOOK-783447, 2019, p. 19-22, https://www.osti.gov/servlets/purl/1576166
"For the tests of 1956, Johnny organized the Hectoton Group into three teams; each team was responsible for designing an atomic device that deviated from the other devices in some way. He instituted a protocol that named each new device after a bird, and the three devices were called the Swan, the Swallow, and the Swift. They were radically different from the Cleo. ... The Swallow came the closest to resembling a nuclear artillery shell. The Swallow’s design had to be strong enough to withstand the high torque and acceleration it would experience after being fired from an artillery tube. ... The smallest device was the Swift. The Swift team was led by an Air Force captain named Jasper Welch, who would eventually rise to the rank of major general. ... With the coming of summer 1956, Johnny moved his entire group to Eniwetok. ... There were huge clams living inside the atoll, and Johnny wanted to take home a large clam shell. ... When he came to the surface for air, Johnny noticed several sharks circling in the lagoon a hundred yards away ... A Hectoton physicist named Larry Germain [Lawrence S. Germain, author of the LLNL history of tactical nuclear weapons and related thermonuclear primary stages, see illustration; above from our compendium of declassified data linked here], who always wore a pair of thick glasses, was treading water nearby, and Johnny asked him to watch out for the sharks and warn him if they began to get closer. ... When he resurfaced, there was no Germain, and Johnny noticed that the sharks were coming closer. He swam back to shore, and spotted Germain lying on the beach. When he asked Germain why he had left his post, the bespectacled physicist responded, “Well, I thought about what you said about there being sharks in the water, and I decided to get out of there.”
"It was time to test the devices, starting with the Swift [0.19 kt Redwing-Yuma, 27 May 1956, 5 inches in diameter, 24.5 inches long, weighed 96 lb.] . It was tested atop a 200-foot tower. It gave a low yield, about one-fourth of what had been expected. This was not an encouraging start. ... they would have to wait and see how the other designs worked. That opportunity came two weeks later, with the test of the Swallow [1.49 kt Redwing-Kickapoo, 13 June 1956, 8 inches in diameter, 28 inches long, weighed 225 lb] atop a 300-foot tower. The mediocre performance of the Swift made the mood tense. ... the Swallow performed well, rendering a yield greater than had been predicted. The Army had wanted a tactical nuclear device, and it looked like they may now have one. Next it was the Swan’s turn. When test day arrived, the same controls that had detonated the Swallow now triggered the Swan, which lit up the South Pacific sky and gave a yield in the upper part of its predicted range of values, which was gratifying [Swan, reported to be a boosted a two-point ignition hollow-pit air-lens flying plate slapper device, aka XW-45, was tested as the 15.2 kt Redwing-Inca nuclear test on 22 June 1956, with a mass of 47.6 kg, a length of 58 cm and a diameter of 29.5 cm. On 2 July 1956 it was used as the primary stage of the 360 kt Redwing-Mohawk test which used a Flute secondary stage. Mohawk was 15 inches in diameter, 46.2 inches long, and weighed 1116 lb]. This was the mothership of their atomic designs – the main hope for the Hectoton Group – and it had performed well. ... At a meeting held back in Livermore in August 1956, Johnny announced, “A study named Robin has been started on a different method of implosion [Dr Peter A. Goetz states the Robin was melon shaped in A technical History of America's Nuclear Weapons, v2, revised edition 2020, p209: "The Robin contained a hollow, boosted, plutonium core that resembled a "thick eggshell" ... Instead of using a shockwave to shape and compress its core ... Robin relied on deflagration ... burning ... at subsonic velocities ... the explosive envelope of the Robin primary was composed of PBX9404 (94% HMX) and its core was composed of alpha-phase Pu239, the densest known allotrope ... 19.89 g/cc"]. It aims to achieve a device characterized by light weight, ruggedness, and moderate efficiency.” ...
"They quickly converged onto a design that was a marvel to study. There were originally two versions of the Robin, Robin A and Robin B. The first A version used enriched uranium as its nuclear fuel, and it was cumbersome. The second version, Robin B, had a plutonium pit and when it was tested, it performed exquisitely. The Robin B was a true descendent to the original Geode concept. It was light and rugged, and it gave a significant yield. When the Robin B team was done, the device could be carried by one man. ... The Robin never showed up in America’s nuclear stockpile; that was not its legacy. It was much more important than that. It became the foundation upon which to build warheads for the future. It was the ultimate fission weapon, the prototype used to build the country’s modern stockpile. [However, Robin primaries were used in the 1963 Lawrence Livermore Lab W47Y2 X1 warhead, with an oralloy (U235) Fife secondary stage, for the Polaris A2 SLBM. In 1965, when tests showed that 75% of these 144 Robins failed due oiled neutron absorbing wire corroding permanently into the plutonium core of the Robin primary - this cadmium-boron wire was supposed to be pulled out by a small electric winch motor automatically before detonation as a safety system to prevent nuclear yield release in accidents - the Robins were replaced by 10kt boosted linear implosion Kinglet primaries. The Polaris A-3 carried three 200kt W58 thermonuclear warheads, the first American deployed devices with spherical oralloy loaded Tuba secondaries, Kinglet primaries and thorium casings. Polaris was important not only for giving a protected second strike capability to the West, eliminating the dangerous need for launch on warning and a first strike to avoid missiles being hit first like sitting ducks in a surprise strike by the enemy, but also for replacing regional land based missile systems. For example, the old vulnerable Jupiter missiles in Turkey which Kennedy removed in "exchange" for the removal of Khrushchev's missiles in Cuba, were simply replaced in March 1963 by the USS Sam Houston SSBN-609, an A-2 Polaris submarine using a base at Rota in Spain. So Khrushchev actually improved American nuclear deterrence by asking for the junk Jupiter missiles to be removed from Turkey!] "
ABOVE: the Russian's took three years to develop their first small-diameter two-point linear (long-axis compression) implosion "Melon" device, without using computers, which was tested with success (full design yield) in March 1956. An illustrated article, The Tsar projectile for nuclear artillery, by one of its developers, Dmitry V. Shirkov (in charge of predicting the yield, not so easy for a radical two point linear implosion device if you don't have any computers!) is linked here, see also the page here.
NEUTRON BOMB AND PAL SECURITY PIN NUMBER SYSTEM:
"The Soviet Union maintained a huge army in Eastern Europe that was poised to launch itself against the democracies of Western Europe, especially West Germany. Its 96 divisions consisted mostly of armored forces and mechanized infantry – tanks and soldiers mounted in armored vehicles. B Division physicists came up with an idea for a weapon that could be used against Soviets tanks in an invasion. Their idea was to attack Soviet tank crews without destroying the surrounding West German countryside by detonating the weapon at a high altitude. The weapon was called an enhanced radiation warhead because it could release more radiation, especially neutrons, aimed at tankers while having a reduced blast. It would deter the Soviet Union from launching an armored attack against the West. Johnny decided that the enhanced radiation warhead qualified as a valid weapon to test in the new operations.
"The RAND Corporation, a so-called “think tank” headquartered in Santa Monica, California, is used by the Department of Defense for studies related to national security. From its earliest days, analysts from RAND visited the Laboratory to observe how the country’s nuclear weapons research was progressing, and true to form, a RAND analyst named Sam Cohen visited Johnny to ask what was new. Johnny described the enhanced radiation weapon they were testing, and Cohen exclaimed, “You’ve invented the neutron bomb!” Cohen went back to his office in Santa Monica and wrote up a report in which he described what he had heard about the new weapon, and he claimed that he had invented it [this is inaccurate and relates to a later meeting in 1962 not Cohen's key visit in 1958, according to Cohen, and Johnny wasn't developing a neutron bomb to end world wars, but cleaner, low yield thermonuclear weapons "Dove" and "Starling" for project Plowshare, and it was him - Cohen - who in 1958, after looking at the "Dove" and "Starling" designs, asked for their neutron outputs off his own back, and then put together the collateral-damage-averting two-stage 1-2 kt enhanced neutron air burst concept for deterrence of invasions!]. The weapon underwent development over the years until it was ready to be deployed with NATO troops. ...
"Six months after the crisis over Berlin, [President] Kennedy flew out to Berkeley to receive an honorary degree from the University of California [23 March 1962] ... The nuclear warheads that Kennedy had relied on when he faced Soviet threats had been designed by these very same scientists, and Kennedy wanted to thank them personally. As Director of the Laboratory, Johnny would be giving the President a briefing to show him the warheads that were part of the backbone of the nation’s defensive posture. ... Full-scale models of the Polaris and Minuteman warheads were placed on demonstration tables, and Johnny showed the President the strategic warheads. After that, Johnny planned to give a pitch for an idea he had conceived the year before concerning the security of tactical nuclear weapons. He had an idea about how to protect the weapons, and he initiated a program to design a sophisticated anti-theft system that came to be called the Permissive Action Link (PAL). ... ; Johnny explained the PAL concept and Kennedy became animated with the demonstration and pulled up a chair and sat before the device. ...
"The President liked the idea and agreed with Johnny’s approach to solving the problem. Kennedy asked his Presidential Science Advisor, Jerome Wiesner, to look at the matter more deeply, and Wiesner replied on May 29, 1962, that the approach seemed to be a good idea and a timely solution to a national security need. On June 6, Kennedy issued National Security Memorandum No. 160, which directed the Department of Defense to install PAL systems into selected nuclear weapons, principally those in NATO. On July 6, 1962, the New York Times reported, “President Kennedy asked Congress today for $23,300,000 to install electronic locks on nuclear weapons in this country and abroad as a safeguard against accidental or unauthorized firings.” "
HERMAN KAHN'S MUNICH ANALOGY FOR NUCLEAR COERCION BY A RUSSIAN DICTATOR
Munich September 30, 1938: in exchange for a worthless paper agreement promising "peace", Chamberlain allows Hitler to invade the German populated part (Sudetenland) of Czechoslovakia, declaring the need to peacefully protect its own foreign nationals (Germans) living in other countries. Big fuss in media: talk of sanctions, weight of world's opinion weighing on shoulders of Hitler to restrain him - proving that appeasement has allowed Britain time to rearm slower than Germany, thereby removing any real deterrent, and reassuring Hitler that we are committed to "peace in our time". (He had already annexed Austria, but that was permitted just like Crimea's annexation by Russia in 2014.) Six months later - after world's media has "moved on" - the remainder of Czechoslovakia was invaded by Hitler (March 1939). Next invasion (12 months after invasion of Sudetenland of Czechoslovakia): Poland (September 1939). Chamberlain has finally drawn a line in the sand (after years of him and his predecessor Baldwin rearming the UK slower than Germany, allowing any hope of deterrence to slip away, by permitting an enemy to go from no threat in 1933 to a bigger military than the UK, requiring UK rearmament, prior to any credible deterrence being feasible*): he finally tells Hitler invading Poland will provoke war. But given the previous farce, Hitler is not deterred by the paltry level of UK rearmament (compared to Germany), and invades Poland.
Note that once the remainder of Ukraine is invaded by Putin - he has already condemned the government of Ukraine as a danger for fighting to defend parts of its own country that border the Russian bear, so everyone can see where the ship is headed - he will be in Hitler's situation in 1939, since Ukraine has a direct border with Poland. The next replay of history will be that "Poland has been a member of NATO since 1999, and NATO presents a threat or antagonism to Russian occupied Ukraine, which must be neutralised to preserve the peace of mind of Putin and his comrades. If NATO tries to defend its members from further Russian peace keeping invasions and conquests, then Putin/Russia will be forced, regrettably, to use its ICBMs etc. to defend itself, and since America has no ABM since the Safeguard system was defunded by Congress anti-nuclear fanatics like Biden in 1975, goodbye democracy." Also note that Putin has more nuclear warheads and Novichok nerve gas than the West. (Until 22 June 1941, Russia was on Hitler's side and jointly invaded Poland in September 1939, contrary to all airbrushed Russian school history books; and all left wing UK school history books! The reality is the secret annex to the 23 August 1939 Russian-German Molotov–Ribbentrop so-called non-aggression pact, which led to the invasion of Poland by Germany and Russia on 1 and 17 September 1939, respectively, according to which Poland was divided up between the two invaders, Russia and Germany; a fact that Russian and left-wing Western pseudo historians have sought to ignore, play down or cover-up. The point is, there is an historical precedent here to Russian aggression in Europe, despite propaganda denying it.)
Russia could invade not only Ukraine but Europe, if you look past troop numbers to the Russian nuclear and chemical missile stockpile in relation to the West's, which has been depleted (Joe Biden as an anti-nuclear senator for decades was always pushing for Western arms reduction, encouraging enemy aggression). Once Ukraine is invaded by Russia, Poland will be on the new Russian border. It's quite possible that if the chips go down and blitzkrieg becomes the order of the day, NATO will collapse. It just doesn't have the firepower of Russia, undermining deterrence. Kennedy deployed 0.02kt yield W54 tactical battlefield nuclear weapons to Europe to deter invasions. (Little Feller I, on 17 July 1962, proved the W54 - reportedly a scaled down 2-point prolate spheroid implosion Swan device - to observer Attorney General Robert Kennedy, in the last ever atmospheric nuclear test at Nevada Test Site, the film of which was only declassified on 22 Dec 1997. Fired by a crew of two using a 155 millimeter launcher, it detonated at a height of burst of 20 feet, some 1.7 miles from the launch point with a 0.018 kt measured yield. An identical warhead was tested as Little Feller II, 10 days earlier, gave 0.022 kt, also demonstrating a W54 yield reliability of 0.02kt +/-10%.) After Nixon decommissioned them, Carter and Reagan replaced them with W79 tactical nuclear warheads, which remained a credible deterrent against invasions (unlike trying to deter the invasion of Crimea by saying you will bomb Moscow) until the Cold War ended. The USSR collapsed. Then people like Biden lobbied successfully to get rid of tactical nuclear weapons in the 90s, and now we don't have a credible deterrent. How can a threat to put sanctions on Putin, or to bomb Moscow as a last resort, deter an invasion of the Ukraine, when he has a bigger nuclear stockpile plus chemical weapons like Novichok? It's insanity. End of story.
We have experience of this insanity from disarmament propaganda by enemies of liberty, freedom and democracy, not just from Hitler's invasions in the 1930s, but from Stalin's invasions in the 1940s and his successors until the Cold War supposedly ended with the break up of the USSR: America had a monopoly on nuclear weapons until 1949, but it failed to make enough, quickly enough and was unable to use nuclear weapons as a credible deterrent to prevent Stalin from seizing half of Europe after WWII. Puppet governments controlled by Moscow (backed up by tank invasions whenever the strings on the puppets broke, e.g. Germany 1953, Hungary 1956, Czechoslovakia 1968) put tanks on the border of NATO. Then, tactical nuclear weapons were needed until the end of the Cold War to prevent invasions. When they were not there, invasions occurred. When they were available, invasions didn't occur. QED. They tipped the balance of risk against aggressors in a way that sanctions and massive retaliation bluffing doesn't. Biden and comrades in the 70s used the old 30s mythology of "arms control" to try to get rid of credible deterrence. The typical argument is that deterring world wars using the credible deterrence of tactical nuclear weapons is "dangerous" to people planning invasions. That's the whole point. The nuclear fear mongering issue of the much higher background radiation in the mile high city of Denver (if you are fanatical about radiation, then why not start by banning mountain climbing, high altitude cities, aircraft, etc, rather than the fallout from nuclear technology?), also occurs with nuclear weapons deterrence: if you think high yield nuclear weapons that could cause collateral damage are a problem, then why not campaign positively for the tactical weapons that deter the invasions that triggered world wars (the invasion of Belgium in 1914, and Poland in 1939) in place of strategic warheads which fail to deter invasions? If we only have tactical nuclear weapons, we can only stop invasions and there can be no escalation risk. In both cases, it's obvious that the anti-nuclear folk are conning the media, successfully as their forebearers did in the 1920s and 1930s. This was the case also in the 1920s and 1930s when poison gas bomb scare mongering was used in the media to successfully prevent credible deterrence, tragically resulting in world war and tens of millions dead. As the Cold War proved, even carrying a big stick is no deterrent if you speak softly to make it appear incredible. The squealing from the pro-Russian so-called anti-nuclear media folk against the W79 neutron bomb 40 years ago proves that was a credible deterrent (they wouldn't have cared otherwise).
The Western media outlook until a few days ago was that the 150,000 or so Russian troops around Ukraine was just the normal Russian military training exercise, pushed nearer the Ukrainian border for added realism, and such numbers are not enough to occupy Ukraine or Europe, so there can't possibly be a real problem, just American bear-baiting propaganda. Not so. Again, as we saw in the Cold War conquest of Eastern Europe, and even before that in the Third Reich era, you don't actually need huge numbers of boots on the ground to successfully invade countries. All dictatorships are by definition a minority controlling a majority - if it were the other way around dictatorship would not be needed since democracy is a numbers competition where the majority tribe or party wins (even if they have to rely on postal ballots). In any case, secret police (Stasi for instance, in East Germany in the Cold War) did the major job of controlling dissent, not Russian boots on the ground. The primary techniques used are political infiltration, coercion, media subversion, propaganda, fear, and political concentration camps/Gulags for dissidents, which massively reduces the need for large numbers of troops. Putin's seizure of Crimea was done using Russian special forces with their insignia removed from their uniforms. There are lots of tricks involved in warfare to reduce the troop numbers required for invasions. Putin's latest one, officially "recognising" the separatist Russian-infiltrated parts of Ukraine bordering Russia and its sphere of influence, doesn't require a million boots on the ground. Like Hitler's annexation of Austria or Sudetenland, you can "invade" with a token force once you have infiltrated it first by stealth. This was the whole point of Hitler's "peace" propaganda machine in the UK in the 1930s, and the USSR's World Peace Council. Invasions occur at first by reasonable appearing salami tactics: small "peace keeping" incursions are then followed by support to rebels until those rebels mount an assisted coup d'etat or declare a separatist state in their region. Then the process is simply repeated to get further slices, until the rebel numbers become big enough for blitzkrieg to be a success.
ABOVE: 1974 USSR nuclear weapons design poster showing critical masses under different conditions, pointing out that using implosion for compressing a subcritical 12 kg mass of U235 makes it critical, compared to needing 48 kg (a 16.8 cm diameter sphere) for a critical mass of uncompressed U235. Switching to Pu239 reduces this by a factor of 2.82, while enclosing it in a 10 cm thick neutron reflector reduces the bare sphere critical mass by a further factor of 3.42. A combination of using both a neutron reflector and core compression can produce better than a 10-fold reduction in critical mass, according to Russian nuclear weapon designers. The simple Russian Sakharov-Zel'dovich elliptical thermonuclear design published by Uwe Parpart in the 15 October 1976 issue of New Solidarity allegedly originates at least in part from the July 1976 disclosures at U.S. labs by Soviet physicist Dr Leonid I. Rudakov, which also led to an earlier 8 October 1976, article in Science, entitled "Thermonuclear Fusion: U.S. Puts Wraps on Latest Soviet Work", page 166. (In March 1976 Pravda claimed Dr Rudakov had solved the clean fusion power problem using implosion principles.) The Rudakov principle demonstrated how hard radiation energy from the primary (fission) stage of a nuclear weapon is reradiated by a plasma as soft x-rays, to compress fusion fuel at the focus of a 1950s Russian nuclear weapon ellipsoidal radiation case. According to Chuck Hansen, the first American nuclear test using this Sakharov-Zel'dovich ellipsoidal radiation case was the Egg design, fired as the successful 250 kt Redwing-Huron shot at Eniwetok Atoll in 1956 (this is according to Sybil Francis, Warhead politics: Livermore and the competitive system of nuclear weapon design page 131; it also used a spherical secondary stage - the L-3 concept referred to by Francis - which wasn't liked by the USA - unlike Russia and Britain - because of the complexity of doing 3-d computer calculations for the geometry spherical isotropic compression in the 1950s; spherical secondaries were first deployed by America in miniature thermonuclear weapons in 1963, namely the 200 kt, 117 kg Polaris warhead W58 and the 170 kt, 115kg Minuteman warhead W62, while Britain and Russia had by then stockpiled weapons with spherical secondard stages for years). Dr Friedwardt Winterberg mathematically analyses the use of an ellipsoidal radiation case with fission and thermonuclear stages at the focii, in his 1981 book The physical principles of thermonuclear explosive devices, Figure 4 (below), explaining how x-rays of varying energies can be mirrored. Even so, you can make paper calculations that are testable in the field, without requiring 3-d computer simulations, as proved by the 1950s British and Russian programmes.
The American insistence on fuller theoretical analysis prior to testing was bureaucratic time-wasting. It was Teller's less dogmatic Livermore that took up the discarded excellent Los Alamos Huron spherical secondary in 1958, testing to develop warheads not unlike today's contemporary designs. The need for complex computer design simulations may be averted by simple "overkill" to compress and ignite fusion charges using x-rays from multiple stages, bombs within bombs like a Russian doll to avoid the need to enhance the primary stage yield using tritium gas with its 12.3 years half-life (as shown, Howard Morland's use of the 1958 lithium deuteride stage idea in his book reproduces an actual design tested in the 1960s called "Swiss cheese", in which the fusion stage contains several separate subcritical lumps of fissile fuel which release neutrons into lithium deuteride, as an alternative to Teller's original cylindrical "spark plug" idea). These weapons are very simple to service, and incorporate "reliability through redundancy", since the multiple fission primary stages allow for reasonable thermonuclear efficiency even if one primary stage fails for some reason. The accompanying official limited distribution Russian nuclear weapons employment manual, Nuclear Weapons - A Manual for Officers, which we obtained (all three editions) from Ukraine, has photos of Russian MIG-15 fighter jets and tanks which were exposed to nuclear tests by Russia (see illustrations below), and many tables and graphs showing the measured blast and radiation effects of 8, 30 and 150 kiloton yield nuclear tests on different targets, plus thermal effects from a 50 kt test, and is linked here - these confidential Russian nuclear weapons capabilities manuals differ drastically from Glasstone's American exaggerations for propaganda on nuclear effects, e.g. Table 3 in the 1961 nuclear test data compilation shows very different data on thermal effects to Glasstone's Effects of Nuclear Weapon. Russian test data from a 50 kiloton burst shows glass only begins to melt at 700-800 cal/cm^2, while white boards only ignite at 150 cal/cm^2 (although they temporarily smoke or char at 40 cal/cm^2)! (Note that in the Russian tables, кал = cal.) The Russians also show how building skyline shadowing stops most direct radiation. We also uploaded extracts from the 128 pages standard Russian manual, How to operate in the conditions of application of nuclear, chemical and bacteriological weapon, by the USSR's Department of Defense, Moscow, which has 99 illustrations, and other Russian manuals linked here, and there is a Russian translation of the Glasstone propaganda book here.
Further reading: a complete analysis of this invasion situation is included in our 2015 detailed review of Kahn's On Thermonuclear War, linked here (in summary, sanctions can escalate such situations into all-out war; so the people talking about "hard-hitting" sanctions, who don't and won't have either a credible nuclear deterrent to prevent invasions or civil defence to withstand enemy threats, are effectively - despite their lies to the contrary - the warmongers). In Chicago, on 5 October 1937, President Roosevelt (Democratic Party) gave his "quarantine the aggressor speech", to destroy fascist dictatorships without the need for military deterrence: it failed since Japan had hard-hitting sanctions placed on it by America, after it started expanding by force prior to WWII, which led to the Pearl Harbor attack and the Pacific Theatre of WWII, instead of peace. If someone is pointing a large nuclear stockpile in your direction and is hot-headed enough to use Novichok nerve agent and Polonium-210 radioactive agent to kill people in the UK during "peacetime", then what is going to happen if you put hard hitting sanctions on them? Their media will present it as being an act of war; it will provide the excuse to escalate the situation. This sanctions idea, like disarmament for peace, is an example of groupthink autism, whereby nonsense propaganda is used to saturate the media to submerge the key facts, just as occurred in the 1930s when the media became obsessed with proclaiming that appeasement would produce "peace in our time". Some relevant extracts from UK declassified Cold War manuals can be found here and the Russian nuclear weapons employment manuals we obtained from Ukraine prior to the invasion are linked here.
(In original Russian: "Эксперты рассказали о причинах переговоров Владимира Путина и Джо Байдена. Санкции России не грозят, а США заинтересованы в диалоге, считает главный научный сотрудник института США и Канады РАН Владимир Васильев. "Американская сторона в этих переговорах заинтересована. На сегодняшний день все эти разговоры о санкционном списке, о еще каком-то использовании санкционного оружия как "Северный поток - 2" или "Список 35", еще какие-то меры, это я называю "формулой развода". ... По сообщению пресс-службы Кремля, Владимир Путин в ходе переговоров заявил Байдену, что Россия заинтересована в получении юридически зафиксированных гарантий, исключающих расширение НАТО на восток и размещение в соседних с Россией странах ударных наступательных систем. При этом в Белом доме утверждают, что Байден на переговорах с Владимиром Путиным не давал ему обязательств, что Украина останется вне НАТО. Президент России Владимир Путин и президент США Джо Байден провели переговоры 7 ноября в режиме видеоконференции.")
If this is accurate, you wish Biden - already under probation from Joe Public for his disastrous withdrawl from Afghanistan last year, allowing that country to become another dictatorship, just the direction Ukraine will go under his brand of useless grandiose sounding "diplomacy" - akin to Chamberlain shaking hands with Hitler and signing worthless bits of paper, but refusing to deter war credibly and effectively for fear of media condemnation by ignorant journalists - had been a bit more "diplomatic" and promised Putin that Ukraine would remain outside NATO, or even outside of the universe: by the time it would enter NATO, Biden would be out of office anyway so what was the big deal? (Appeasement is ineffectual sanctions; appeasement is not about successfully averting war by making agreements that can later be terminated if necessary!) Biden thankfully can only serve two terms maximum, even if Trump doesn't get back in next time, and American Presidents hardly bother to honour the promises made by their prececessors, even if they are members of the same party. E.g., Truman renegaded on Roosevelt's wartime promise to Britain to continue postwar nuclear weapons collaboration. Britain then had to independently develop its own fission and thermonuclear fusion weapons until collaboration resumed in 1958! If America can do that, it could have given some worthless paper promises to Putin, to keep him out of Ukraine. The Chamberlain appeasement situation was the exact opposite of this: Sudetenland was given to Hitler in exchange for a worthless paper promise from Hitler!
_________________________________________________________
UPDATE, 27 February 2022: Putin puts Russia's nuclear forces on alert, cites sanctions - By Yuras Karmanau, Jim Heintz and Vladimir Isachenkov, Associated Press in Washington post, 27 feb. 2022 - KYIV, Ukraine — "In a dramatic escalation of East-West tensions over Russia’s invasion of Ukraine, President Vladimir Putin ordered Russian nuclear forces put on high alert Sunday in response to what he called “aggressive statements” by leading NATO powers. The order means Putin has ordered Russia’s nuclear weapons prepared for increased readiness to launch, raising the threat that the tensions could boil over into nuclear warfare. In giving it, the Russian leader also cited hard-hitting financial sanctions imposed by the West against Russia, including Putin himself."
This report, by Associated Press in the Washington Post, confirms sadly that so far Putin has responded to sanctions by following the predictions made above, escalating his nuclear weapons readiness for war to counter the sanctions with a nuclear threat, akin to what happened when Japan responded to hard-hitting American oil sanctions against it for its 1930s invasions prior to its attack on an American Pacific military base located at Pearl Harbor. This is the whole problem with the arms control situation. Supplying arms to the Ukraine Government to defend itself against Russia could easily be construed to Putin, if he so chooses, as essentially an act of war against Russia, deserving retaliation. Everything the "liberal elite", the left wingers headed by President Biden, does is always at best autistic lunacy that escalates the danger we face. While the BBC may claim that "Putin is isolated"**, he has a larger nuclear force than us, and also powerful nuclear allies in China. It is simply untrue that sanctions will solve the problem; they escalate a crisis into a bigger war. Carpet bombing of civilians, used by Democratic President Johnson in Vietnam, was the same kind of autism; instead of kicking enemies into surrender, such actions as sanctions and attacking civilians just hardens enemy aggression more.
_________________________________________________________
**(Footnote): The 1930s media also claimed incorrectly that Hitler was isolated (he had allies in Italy, Japan, etc.), but such lies in the "free" press helped to back up liars in the UK Government like Baldwin and Chamberlain and their populist lunatic policies for "peace in our time" which also lacked any credible deterrent, and just escalated the threats, encouraging genocide, not peace. Sir Norman Angell's Great Illusion argument that economic interdependence of nations prevents escalation in war is precisely reversed by the use of heavy economic sanctions against Russia, which cuts off the supposedly peace-keeping economic interdependence of nations and pushes it into the position of Japan in December 1941 and of Germany in September 1939 (thanks to Roosevelt's 1937 "quarantine the aggressor" theory). Irrational acts, not surrender, is what human nature usually produces when cornered and isolated, despite groupthink brainwashing arguments to the contrary, which were used to determine policy in the Vietnam War and recently in Afghanistan. You need to accept enemy mentality as it exists, and not "put yourselves in the enemy's shoes", if your way of thinking lacks the paranoia, cultural mentality, and aggressive nationalism of an enemy. Russia is not completely isolated anyway, due to its allies in China, North Korea, et al. The latest ideas on fighting the war in Ukraine being mooted by the BBC pyschotics/pundits centre around allowing Ukrainian pilots flying missions to bomb Russian forces in EU funded aircraft from airbases in NATO country Poland, while claiming that NATO is not involved. Again, the pressures of this kind provide excuses for Putin, if he wishes, to escalate it to WWIII at a time and in a way of his choosing, with the factor of surprise in his hands. Threatening to bomb the Kremlin suffers from the risk that Putin could move to a bunker elsewhere, even if the bunker under the Kremlin is really at risk bearing in mind the Russian ABM system around Moscow that can knock down incoming warheads (lacking from Western cities) and the nuclear crater sizes exaggeration scandal, which reduces the ground shock and cratering destruction to underground targets due to the ignorance in the 1977 Glasstone and Dolan Effects of nuclear weapons book about the work done against gravity in excavating large craters.
ABOVE: 1986 Russian civil defense manual showing the shelters and evacuation plans which are in many ways similar to British efforts in 1939 prior to the British declaration of war on Germany two days after it invaded Poland. Note that various authors of American Scientific American articles argue that the evacuation plans exist "largely on paper" as if that somehow allows them to be ignored - just as the 1939 British "Operation Pied Piper" plans to evacuate kids from target areas for civil defence prior to the declaration of WWII against the Nazis - existed on paper until needed. But that didn't prevent kids and other vulnerable people, such as the pregnant, from being evacuated from London on 1 September and war declared two days later on 3 September 1939. The point we are making is that, as Herman Kahn argued, Hitler declared peace on Britain not war, and it was Britain that had to declare war first, and it first evacuated the likely bombing target of the most vulnerable using the "paper" evacuation plans to allow it to declare war on the Nazis, something that would have been or at least seemed more dangerous without such an evacuation first. The history of Russian civil defense is interesting, since to the Russians (unlike everyone else on the planet), both World Wars led to victories of sorts: WWI caused the revolution of October 1917 which replaced the Tsar with Lenin, while WWII led to the great expansion of the Russian Empire to include half of Europe, allowing resources to be seized which enabled rapid progress, from MIG jets to fission bombs in 1949 and thermonuclear two stage weapons in 1955, then the first satellite in space in 1957 and the first human in space in 1961. It is simply untrue that all Russians view WWII as being the disaster that it is portrayed for Britain. (Russia actually achieved a victory that included territorial expansion and corresponding financial gains, unlike certain other countries that lost Empires due to WWII.) According to Professor William R. Kinter and Harriet Fast Scott's 1968 book The Nuclear Revolution in Soviet Military Affairs (University of Oklahoma Press, pages 184-191), the Russian Marshall V. I. Chuikov, who was made chief of civil defense for the USSR after stopping the Nazis at Stalingrad in WWII, and later advising Chiang Kai-shek and also founding the Whampoa Military Academy, in 1966 wrote an article in the Russian journal Military Knowledge, stating that civil defense allows a Russian victory in WWIII:
"The outcome of nuclear rocket war will now be decided not only on the battlefield, it will in significant measure be predetermined by strikes on the rear areas and on important political and economic centres. Victory in such a war will depend to a large degree on the ability of the state to survive."
- Quotation from William R. Kinter and Harriet Fast Scott's 1968 book The Nuclear Revolution in Soviet Military Affairs, University of Oklahoma Press, pages 184-5. (Emphasis added to words which are totally taboo here in the West in connection with all things "nuclear". Note that co-author Harriet Fast Scott, a research agent/spy fluent in Russian, lived in the USSR for years in the 1960s since her husband was assigned there as U.S. air attache.)
Kinter and Fast Scott point out on page 185 of The Nuclear Revolution in Soviet Military Affairs:
"Military Knowledge, the magazine in which the [Chuikov] article appeared, is the official monthly journal of civil defense. There is nothing comparable with this publication in the United States ... The expensive, elaborate family shelters - advertised in the United States some years ago - are unknown. A practical, inexpensive approach for protection measures, using materials readily available, is stressed. It is hardly appreciated in the United States that the Soviet Union already possesses the world's finest shelters ... These are the deep, elaborate subways in five of the largest cities - Moscow, Leningrad, Kiev, Tbilisi, and Baku. Many sections of the subways run well over 100 feet below street level and are provided with heavy blast doors ... A large number of the total inhabitants of Moscow and Leningrad could be provided shelter in their subways alone." (Britain installed some similar deep shelters in various London tube stations.)
Regarding the Chuikov doctrine on the ability to achieve a "victory" in nuclear war by being better prepared for any eventuality than the opponent, the side which is better able to survive a nuclear war (by civil defense) can be considered the winner: this Marxist concept of war also prevailed successfully in Vietnam, where the Vietcong dug deep tunnel shelters and left civilian kids to be napalmed in the open for left-wing Western propaganda. It worked, they won in Vietnam using that strategy. This is the very opposite of the "knockout blow" mythology that prevailed in Germany in 1914 and 1939, and also in the West during the Vietnam War, but not the 1st Cold War as a whole, where the West achieved victory and the USSR defeat, through the West's surviving longer than the increasingly bankrupt USSR. Herman Kahn pointed out in the 26 June 1959 U.S. Congressional Hearings on the Biological and environmental effects of nuclear war, that Germany did not start WWI or WWII by a direct attack on Britain, and that Germany planned for a short "knockout blow" military conquest; in both cases it was Britain that declared war on Germany first, not vice-versa. In other words, "Type I Deterrence (deterrence of a direct attack on Britain)" did not fail in either 1914 or 1939. Only "Type II Deterrence (deterrence of an act of provocation, e.g. the invasion of a third party)" failed. So a country starting WWIII, on the basis of WWI and WWII experience, does not need to directly bomb London or New York. Put another way, strategic nuclear weapons, if they had existed in 1914, would have no more deterred the invasion of Belgium then, than they deter the invasion of Ukraine today. For victory you need to be capable of fighting and surviving sufficiently either a surprise attack or long war of attrition, regardless of whether that is an economic cold war via an arms race, or a hot war involving any kind of weapon.
The strategic nuclear deterrent's role is purely Kahn's debunked Type I deterrence - a fallacy due to the Western obsession with "knockout blow" mythology - which also prevailed in the West in the 1930s where the media was filled with hype claiming that single gas or incendiary aerial attacks on cities would induce defeatism and immediate surrender. This was a travesty of logic which ignores precisely those situations - indirect attacks - that triggered both World Wars. Deterring indirect attacks like sinking the Lusitania in 1915, invading Belgium in 1914, bombing a Pacific island naval base at Pearl Harbor in 1941, or invading Poland in 1939, requires not Type I but the more difficult Type II deterrence, tactical nuclear weapons, since conventional weapons failed to deter both world wars and strategic nuclear weapons have not proved to be a credible deterrent against invasions of third parties. This is because the mobilization of conventional conscripted large armies or tank columns to borders for deterrence of large scale invasions is seen as an act of aggression, whereas nuclear weapons of significant deterrent power are small enough to be continuously available aboard submarines and in missile silos and iglo bunkers on airfields, ready at all times without the trigger-happy 1914-crisis-escalating massive mobilizations that set off World War I. As General Boisdeffre stated lucidly to Tzar Nicholas in 1892, the mobilization of conventional weapons to try to deter world war has the opposite effect because the highly-visible mobilization of the relatively bulky conventional weapons and massive armies is naturally a massive escalation rather than a deterrent, causing immense crisis instability:
"THE MOBILIZATION IS THE DECLARATION OF WAR. TO MOBILIZE IS TO OBLIGE ONE'S NEIGHBOUR TO DO THE SAME ... OTHERWISE, TO LEAVE A MILLION MEN ON ONE'S FRONTIER, WITHOUT DOING THE SAME SIMULTANEOUSLY, IS TO DEPRIVE ONESELF OF ALL POSSIBILITY OF MOVING LATER; IT IS PLACING ONESELF IN A SITUATION OF AN INDIVIDUAL WHO, WITH A PISTOL IN HIS POCKET, SHOULD LET HIS NEIGHBOR PUT A WEAPON TO HIS FOREHEAD, WITHOUT DRAWING HIS OWN ..."
The mad emergence of nuclear parity, in the late 1960s and early 1970s, occurred after Robert S. McNamara used now-discredited computerised nuclear war effects models (with no more sensible equations than those he used to lose the Vietnam war, i.e. ignoring Russian civil defense just as the improvised conventional war underground shelters of the Vietcong were ignored) to determine nuclear deterrence stockpile levels. The Russians then produced more weapons than America into the 1970s, and America responded with the neutron bomb and arms control treaties for strategic weapons. This was a reversal of the American nuclear superiority behind the amicable resolution of the Cuban missiles crisis by Kennedy in 1962, a factor pointed out by General LeMay in his 1968 book America is in Danger. (Where the left-wing disarmament-biased "historians" analyze the lessons of the Cuban missiles crisis, they deliberately ignore the massive U.S. nuclear superiority which existed in 1962, and its positive effects on Russian decision making, just as they ignore Feis' argument in Japan Subdued, that the emotional aspects of nuclear weapons effects in August 1945 tipped the balance against accepting a dishonorable surrender; in other words, although Japan knew it was defeated and the nuclear attacks were in that sense totally unjustified, emotionally they needed an "excuse" to hoist the white flag after so much suffering, and this saved 200,000 Yanks earmarked for an invasion of the Japanese home islands as well as 1,500,000 Japanese lives.)
There is a compendium of classic 1960s and 1970s arguments for civil defense, and their political suppression by left-wingers and fools, in Nobel Laureate Dr Eugene P. Wigner's Collected Works, part B, volume VIII, edited by Jagdish Mehra (Springer, 1998, 258 pages). Wigner on 28 April 1976 testified before the U.S. Congressional Hearings of the Joint Committee on Defense Production (page 144 in their printed hearings, online version is LINKED HERE) that the new Russian evacuation plans - as shown in its 1969 Civil Defense Manual (translated as ORNL-TR-2306, Oak Ridge National Lab.) - are very effective (the Russian civil defense plan includes only essential workers commuting into cities for 12-hour shifts, and using shelters):
"Indeed an easy calculation shows that, if the USSR carries out its city evacuation plans, the total number of casualties that all the nuclear weapons in our missiles could cause would be a good deal less than 50% the losses they suffered in World War II. A reasonable estimate, based on the Oak Ridge [National Laboratory] test of a blast resistant 'expedient shelter', described in the USSR civil defense handbooks, gives for the loss which our missile carried nuclear weapons could cause, about 3% of the USSR population. What about our own situation? ... An evacuation plan [costs] $1.2 billion .... a blast resistant shelter system similar to that of China ... would cost around $35 billion."
In 1979, in a joint article with hydrogen bomb advocate Dr Edward Teller in the U.S. Senate Congressional Record (2 August 1979, page S-11490), Wigner points out that Kahn's Type I deterrence is inadequate to prevent war (Type I is also called "mutual assured destruction", if both sides have parity via "arms control" delusions): "... I believe that the so called Mutual Assured Destruction is nonsense, because suppose even if the attacked nation could retaliate, if the other nation pretends that it does not believe it and makes a demand, is there any point in resisting? What good does it do if it can destroy hundreds of thousands of the aggressors' lives ..."
In his 26 May 1964 address to Mercer County NJ Civil Defense organization (reprinted in his Collected Works, part B, Vol. 8, p35 et seq.), Wigner explains that "people who are against Civil Defense often have some element of frustration ... and they find more easily time for, and outlet in, their opposition," as explained by Robert Waelder's article Protest and Revolution Against Western Societies, in M.A. Kaplan (ed), The Revolution in World Politics (New York, 1962, p 18), i.e. it is the same as the mechanism for Marxist agitators, some of which are openly Marxist and others pretend to be libertarian while remaining faithful to the bigoted dictators. Wigner's address continues: "Much more literature - I think 80% - is against than for Civil Defense and much of it is completely irresponsible. A few weeks ago I read an article in the Bulletin of the Atomic Scientists in which the author said that a complete fallout [cheaper than blast] shelter program would cost $50 billion. Now $50 billion is more than would be spent on the complete blast [and fallout] shelter program which I mentioned [$35 billion]. But ... who will contradict it?"
In Publication 82 of the American Association for the Advancement of Science, Civil Defense, 1966, edited by H. Eyring, Wigner remarks on page 121: "Dr Rapoport said, in a note to the Bulletin of the Atomic Scientists, that it is possible that surrender to Hitler would have led to fewer deaths ... My view is the opposite in this case: I believe that if the West had shown clear resolve and determination from the start, WWII could have been averted."
After Leon Goure wrote his May 1972 report, "Soviet Civil Defense - urban Evacuation and Dispersal" (Centre for Advanced International Studies, Miami University, DTIC report AD0745136), Wigner and J. S. Gailar wrote in their joint article "Russian Evacuation Plans - the Fears they Create" in the September-October 1974 issue of Survive (v7, n5, pp 4-5): "If the leadership of the USSR should change and become more aggressive, it would have, under the present circumstances, a terribly tempting option: to stage an evacuation and to provoke a confrontation when this is completed." Wigner later testified to the U.S. Congressional Hearings of the Joint Committee on Defense Production, Civil Preparedness and Limited Nuclear War (28 April 1976, pp 143-7) that the principal danger: "is the possibility of the USSR evacuating its cities, dispersing their population, and the making demands on us, under the threat of a nuclear attack, approximating those made by Hitler on Czechoslovakia which led to the Munich Pact."
The only reply Wigner received was a nonsense filled 11-page article attacking all these lessons from Russian Civil Defense, headed "Limited Nuclear War" by Sidney D. Drell and Frank von Hippel, and published in the November 1976 issue of Scientific American, the editor of which, Dennis Flanagan, refused to publish Wigner's rebuttal, entitled "We heartily disagree", just as Kahn's rebuttal to the nonsense review of his book on Civil Defense in 1961 had been refused by Scientific American, leading Kahn to expand it into his 1962 book "Thinking about the unthinkable". Wigner's and A. A. Broyles rebuttal to Scientific American was finally published instead as "We heartily disagree" in the Journal of Civil Defense, v10, pp. 4-8, July-August 1977 issue, pointing out that the Russian casualties with civil defense would be 4% on Wigner's unclassified estimate or 2% using T. K. Jones's classified data estimate (utilizing secret data on the survival of foxholes in nuclear tests, in the 1972 DNA-EM-1 Capabilities of Nuclear Weapons), and that the Russian improvised lined, covered trench shelters survive a peak overpressure of 40 psi as well as heat flash and fallout radiation, and adds that contrary to the nonsense in Scientific American, the Russians did test their plans by evacuating the city of Sevastopol in a drill which led to improvements in their plans.
H-bomb proponent Edward Teller, Eugene Wigner, and A. A. Broyles in May 1973 had jointly authored the American Security Council report, "Without civil defense we are in a glass house", which basically argues that you can't have a deterrent for world war if you are not prepared to use that deterrent when your bluff is called. If you are in Chamberlain's position in 1938 or Baldwin's in 1935, you are scared of using the deterrent because it is like "throwing stones in glass houses", because - if you can't shelter people because you refuse to have shelters and you also won't have a plan to evacuate kids from London (Operation Pied Piper, 1939) before you declare war - then you can easily be scared and coerced by Hitler or other dictators, who can see clearly that your "deterrent" is a complete bluff and totally, pathetically useless, because a weapon you can't use is not a credible deterrent. Naturally, as we keep repeating on this blog, this is what the defeatists who love Putin and other dictators want since surrender has two vital steps: (1) get rid of the shield (civil defense) since that makes the sword credible as an alternative to disarmament, and (2) point out that a sword without a shield is an incredible deterrent that is useless, so we had better disarm (and surrender)! Arms control delusions like supposed "parity" (a balance of weapons on both sides, as if democracies need detering like dictatorships), when one side has credible civil defense and the other doesn't, is like a duel between two people, similarly armed, but with one wearing body armour and the other totally unprotected! Not on that, but the dictator is the one wearing the body armour!
ABOVE: long-haired scientist Thomas K. Jones, better known as T. K. Jones, (pictured testifying before the Joint Committee on Defense Production, in Science magazine, 10 December 1976 after his Congressional Testimony raised the wrath of crackpot Scientific American and Bulletin of Atomic Scientist fans) was the "fall guy" of Reagan's civil defense, doing the explosive tests for Boeing Corporation on Russian civil defense shelter designs and testifing on their consequences for strategic nuclear deterrence - basically debunking strategic nuclear deterrence and McNamara's/Glasstone's totally fake news on urban nuclear weapons effects entirely, since 98% of Russians would survive the US nuclear stockpile when dispersed in shelters - which inspired Cresson Kearny's Oak Ridge National Laboratory manual, Nuclear War Survival Skills. President Ronald Reagan, prior to his election as US President, was leaked secret CIA reports on Russian civil defense tests of shelters and evidence of their tests of city evacuation plans for instance by evacuating Sevastopol in Crimea and also, in 1975, Lytkarino (a suburb of Moscow containing 40,000 people). A clue to who helped him was shown by Reagan's decision to controversially appoint T. K. Jones as Under-Secretary for Defense for Research and Engineering! A book was then published called With Enough Shovels: Reagan, Bush and Nuclear War, ignoring the key scientific evidence entirely, and merely trying to ridicule Reagan's appoinment of T. K. Jones (who is quoted on the front cover), as a left wing Democratic supporting political instrument - like Duncan Campbell's similarly vacuous War Plan UK. This was left-politics versus hard science. It often appears to work because Mr Joe Public loves a tall-story fairy tale!
If proof of this is needed, Robert Scheer, a fellow in arms control at Stanford University and the author of With Enough Shovels: Reagan, Bush and Nuclear War, became "Truthdig" editor-in-chief, a propagandarist who claims that ending WWII with nuclear weapons made Truman guilty of "the most atrocious act of terrorism in world history", so he needs to check his facts on the numbers gassed in the Holocaust, or starved in Ukraine by Stalin, unless he denies those deliberate acts of terrorism like the other left wing Holocaust deniers who confuse racism and anti-racism, terrorism and anti-terrorism. When you actually check the facts: (1) Secretary Stimson (U.S. Secretary of War) knew he has a secret nuclear weapons program of investment of billions of dollars to justify to Congress after WWII ended and didn't want to hold back using the bomb for that reason, so he promoted Hiroshima as being a military target (it did have military bases, particularly at Hiroshima Castle just north of ground Zero, but it was also a highly populated civilian city), (2) Hiroshima's air raid shelters were unoccupied because Japanese Army officers were having breakfast when B29s were detected far away, says Yoshie Oka, the operator of the Hiroshima air raid sirens on 6 August 1945, (3) Colonel Tibbets, former bomber of Germany before becoming the Hiroshima pilot as commander of the 509th Composite Group, explains how his pilots and crew were ridiculed heavily for lack of accomplishments, while preparing for weeks on Tinian Island. According to Tibbet's own book The Tibbets Story a poem was published before Hiroshima called "Nobody knows" lampooning the 509th's results: "Nobody knows. Into the air the secret rose; Where they're going, nobody knows; Tomorrow they'll return again; But we'll never know where they've been. Don't ask us about results or such; Unless you want to get in Dutch. But take it from one who is sure of the score, the 509th is winning the war. When the other Groups are ready to go; We have a program of the whole damned show; And when Halsey's 5th shells Nippon's shore; Why, shucks, we hear about it the day before. And MacArthur and Doolittle give out in advance; But with this new bunch we haven't a chance; We should have been home a month or more; For the 509th is winning the war." Tibbets was therefore determined create maximum effects after his group had been ridiculed at Tinian Island for not attacking Japan during weeks of preparations on the island, rehearsing the secret nuclear attacks while other B29s were taking took flak trying to bomb Japan into surrender with conventional bombs. He writes in The Tibbets Story that regular morning flights of small groups of weather and phototographic survey planes that did not make significant attacks over possible nuclear target cities, helped to reduce civil defense readiness in the cities, as well as reducing the air defense risks, since Japan was rationing its use of its limited remaining air defense in 1945.
The November 1976 Scientific American anti-civil defense article claimed that civil defense was discredited since: "In the 1960s the US adopted a strategic policy giving top priority to the prevention of nuclear war through deterrence ...", to which Wigner and Broyles responded to this claim in "We heartily disagree" in the July-August 1977 Journal of Civil Defense: "How do you deter an attack unless you convince an enemy that you will fight the war that he is starting?"
Dictators often start wars which their people don't need: the Persian war against the Greeks, Hannibal's war against Rome, the Tartar's invasions of Europe, the Turks' invasion of Hungary, the invasions of Napoleon. You have to accept that aggression is not necessarily a completely rational activity! All that counts for deterrence is that it is credible. If you don't prepare to fight with strategic nuclear weapons, then they are just a pointless bluff, a paper tiger as the Chinese put it, not a credible deterrent. Which is precisely what the disarmers want, of course, since nuclear parity, with the shift away from credible nuclear deterrence to incredible foolery, is only one step away from admitting the uselessness of the strategic nuclear stockpile, disarming and surrendering!
UPDATE (10 March 2022): A commenter on this blog post states:
Western Trade Pressure on the Soviet Union, An Interdependence Perspective on Sanctions, Springer, 1991, by David W. Hunte, pp 14-15:
Economic Sanctions: Pre-World War II Through Cold War
"In 1925, British Foreign Secretary Austen Chamberlain stated in the League of Nations: ‘The great advantage of economic sanctions, is ... they do not involve the resort to force.’ The commonly held view was that economic sanctions were the perfect weapon to pressure states into compliance without blood being spilt or lives lost. By 1980, however, Adler-Karlsson had reached a different conclusion: economic sanctions as instruments of foreign policy almost never worked. ... . In both Britain and France, the situation was one of choosing the least undesirable alternative."
Just one final thought on Kennedy's experience: apart from putting civil defense "nuclear shelter" signs on public building basements and putting geiger counters, food, water and emergency toilets into them to enable America to take shelter if the chips go down, apart from sending his brother to Nevada test site to watch the test firing of the W54 Davy Crocket battlefield tactical nuclear deterrent weapon in 1962, apart from standing firm on the Cuban blockage in October 1962 (instead of appeasing Khrushchev, and note that the obsolete pile of junk he removed from Turkey, the highly vulnerable liquid-fuelled old Jupiter missiles, were obsolete anyway and due to be replaced by less vulnerable Polaris sub in the Med), and apart from approving the final series of high altitude nuclear tests, Operation Fishbowl, which revealed the magnetic dipole EMP, Kennedy also rejected the economic trade sanctions against the USSR which could have forced another war like the sanctions of the 1930s:
ABOVE: John F. Kennedy's Why England Slept manuscript dated 25 May 1940 (CREDIT: JFK LIBRARY); notice the statement above right that his conclusion is that the war was the inevitable result of the slowness of the conversion of the British disarmament policy into a policy of rearmament! John F. Kennedy's college thesis on the need for deterrence and civil defence to make it credible in the face of enemy threats and aggression (a big stick in the hands of a goliath is useless if the enemy is a David with slingshot that can stun the goliath with a stone to the forehead, allowing victory, so you need some defensive armour to make the big stick a credible deterrent rather than mere bluff that can be easily neutralised by any smaller enemy due to your vulnerabilities), Why England Slept, is still worth more than all the sanctions and peaceniks literature ever written, explaining his often forgotten speech on civil defence as a national necessity for credible deterrence of war, given as United States President to a Joint Session of Congress precisely 21 years later to the day from the completion of his book (speech on 25 May 1961, precisely 21 years to the day after the 25 May 1940 date on his manuscript above):
"No role in history could be more difficult or more important. We stand for freedom. ... I am here to promote the freedom doctrine. ... the adversaries of freedom ... send arms, agitators, aid, technicians and propaganda to every troubled area. But where fighting is required, it is usually done by others - by guerrillas striking at night, by assassins striking alone - assassins who have taken the lives of four thousand civil officers in the last twelve months in Vietnam alone - by subversives and saboteurs and insurrectionists, who in some cases control whole areas inside of independent nations. ... We stand, as we have always stood from our earliest beginnings, for the independence and equality of all nations. This nation was born of revolution and raised in freedom. And we do not intend to leave an open road for despotism. ... Military pacts cannot help nations whose social injustice and economic chaos invite insurgency and penetration and subversion. The most skillful counter-guerrilla efforts cannot succeed where the local population is too caught up in its own misery to be concerned about the advance of communism. ...
"One major element of the national security program which this nation has never squarely faced up to is civil defense. This problem arises not from present trends but from national inaction in which most of us have participated. In the past decade we have intermittently considered a variety of programs, but we have never adopted a consistent policy. Public considerations have been largely characterized by apathy, indifference and skepticism ... this deterrent concept assumes rational calculations by rational men. And the history of this planet, and particularly the history of the 20th century, is sufficient to remind us of the possibilities of an irrational attack, a miscalculation, an accidental war, which cannot be either foreseen or deterred. It is on this basis that civil defense can be readily justifiable - as insurance for the civilian population in case of an enemy miscalculation. It is insurance we trust will never be needed - but insurance which we could never forgive ourselves for foregoing in the event of catastrophe. Once the validity of this concept is recognized, there is no point in delaying the initiation of a nation-wide long-range program of identifying present fallout shelter capacity and providing shelter in new and existing structures. Such a program would protect millions of people against the hazards of radioactive fallout in the event of large-scale nuclear attack. Effective performance of the entire program not only requires new legislative authority and more funds, but also sound organizational arrangements. Therefore, under the authority vested in me by Reorganization Plan No. 1 of 1958, I am assigning responsibility for this program to the top civilian authority already responsible for continental defense, the Secretary of Defense ... no insurance is cost-free; and every American citizen and his community must decide for themselves whether this form of survival insurance justifies the expenditure of effort, time and money. For myself, I am convinced that it does."
ABOVE: Hitler propaganda and coercion so called peace offers in October 1939 and March 1940, because he knew that Britain's Secretary of State for Foreign Affairs, Lord Halifax, was keen on trying to negotiate a peace deal with the Nazis rather than face up to a repeat of WWI, particularly after Britain's defeat in France at Dunkirk in the face of the overpowering German Panzer attacks (radio propaganda, aided by plenty of whisky and cigars, from Churchill portrayed this retreat and evacuation from Europe as being a miracle, but although losses were minimised - thanks not to Churchill's planning but to emergency improvised evacuation across the channel using small private boats from England - Hitler won the actual battle and successfully drove the British Expeditionary Force from France). Russia in the 1st Cold War set up the World Peace Council in Moscow to fund and help Western nuclear disarmament movements to try to make its domination of the West possible by removing W79 neutron bombs etc, leaving us without a credible deterrent against Russian invasions. It simultaneously made peace propaganda offers to end war by collaboration with dictatorships, an offer that appealed to many idealists who believed it, as Lord Halifax believed Hitler's repeated peace lies. We can expect Putin to make peace promises as a propaganda tool. If he actually wanted peace he would not have invaded Ukraine.
March 14, 2022 5:04 PM GMT https://www.reuters.com/world/un-chief-says-prospect-nuclear-conflict-back-within-realm-possibility-over-2022-03-14/
U.N. chief: prospect of nuclear conflict back 'within realm of possibility' over Ukraine By Humeyra Pamuk
March 14 (Reuters) - United Nations Secretary-General Antonio Guterres on Monday sounded the alarm over Russia raising the alert level [weeks ago] for its nuclear forces after invading Ukraine, describing it as a "bone-chilling development." "The prospect of nuclear conflict, once unthinkable, is now back within the realm of possibility," Guterres told reporters, and repeated his call for an immediate cessation of hostilities. Russia's invasion of Ukraine that began on Feb. 24 has so far sent more than 2.8 million people fleeing across Ukraine's borders and trapped hundreds of thousands in besieged cities while triggering broad Western sanctions on Russia. [Actually, the so-called UN, better called the non-united nations, contributed to the war by its repeated calls for nuclear disarmament, which has had precisely the effect John F. Kennnedy found when he wrote Why England Slept from his experience in London with his dad, the American Ambassador to Britain, when deterrence failed due to Nazi propaganda on war devastation and poison gas on cities for disarmament, defeatism, and a Third Reich conquest using a minimal military force.)https://www.ft.com/content/6cf7229b-1aa7-435e-84d9-e3c7a094350d#post-5a7c0648-f48b-4cfb-a163-95b922713201 Financial Times, 16 March 2022. Zelensky pleads with Biden for no-fly zone or fighter jets. James Politi in Washington. Ukraine’s president Volodymyr Zelensky pleaded for the US to enforce a no-fly zone or provide fighter jets or other means to fend off Russia’s attack on his country, in a virtual address to members of Congress on Wednesday. Zelensky urged US lawmakers to impose harsher economic sanctions on Moscow ... He called on Americans to remember the attacks on Pearl Harbor and September 2001, saying “our country is experiencing the same thing every day right now”, and showed a video of the missile attacks and shelling destroying Ukrainian cities. ... At the end of his address, Zelensky directly addressed US president Joe Biden in English, saying: “I wish you to be the leader of the world. Being the leader of the world means to be the leader of peace.” (Loon's "peace" is the nuclear deterrent-lacking world of 1914 or 1939.)
ABOVE: Hiroshima ground zero showing surviving concrete buildings amid the debris from now-obsolete wood frame (with tiled roof) buildings that burned in a firestorm that developed 30 minutes after the bombing, not instantly as claimed in approximately 100% of newspaper and TV fake news propaganda on nuclear weapons for disarmament - a Los Alamos nuclear weapons jobsworth and coward called Dr Harold Agnew exposed only in SECRET classified documents the exaggerations of nuclear weapons effects on people on modern concrete city buildings in Hiroshima with a "Confetti argument" - see the originally SECRET Los Alamos report LA-14066-H, Tracing the Origins of the W76: 1966-Spring 1973 (U) by Betty L. Perkins, thereby preventing widespread public understanding of the truth, and so enabling anti-nuclear media dominating anti-civil defence pro-disarmament pro-dictatorship liars to deceive the world about nuclear weapons capabilities just as the 30s poison gas media dominating anti-civil defence pro-disarmament pro-dictatorship liars to deceive the world about the Nazi threat to gas bomb all modern cities, etc. This anti-nuclear disarmament propaganda effort is still covering-up the hard scentific facts on nuclear radiation effects for everything from medicine to nuclear power, such as the extensive evidence (see the graph below from the still-maintained website of U.S. Government's radium dial painter dos-effects project investigator, the late Dr Robert E. Rowland, 1923-2017) that there is a dose-rate threshold for cancer of approximately 100 micro-Sieverts per hour or 10 mR/hour in old units (from an intake of 100 microcuries of radium-226 alpha emitter or its equivalent), summarised as follows by study leader Dr Robert Rowland in his published 1995 Oral History interview:
ABOVE: Blast duration effects on cube root scaling are only important at low yields, not high yields, as observed for house damage in Britain, based on actual observations, not faked "theoretical analyses" used for propaganda for anti-nuclear disarmament scare mongering, which is designed to try to discredit civil defense using lies in order for disarmament and surrender to be the "only option" for survival.
The blood of the Ukrainian kids must be partly on the hands of those who permitted the circulation of nuclear deterrent lies to remove Ukaine's nuclear deterrent against Russian aggression. What a terrible people keep the truth secret, thereby allowing public deceptions by political left-wing thugs for nuclear disarmament to enable dictatorships to launch lethal invasions with effective impunity. Other warhead histories by Betty Perkins include LA-13755-H: Tracing the Origins of the Modern Primary: 1952-1970 (U), LA-12950-H: Why Nougat? (U) Understanding the Events Leading to the Los Alamos Scientific Laboratory's First Full-Scale Underground Test Series and Related Considerations (U), and LA-12393-H: The 1959-1961 TA-49 Experiments and Related Considerations (U).. Don't expect to ever see anything like this published on the front page of any Western so-called newspaper or as the lead item in any Western TV "news" show. They carefully screen out anything that upsets the nuclear warmongers who don't care about provoking another war through disarmament lies, as they did in the 20s and 30s, because the Western public want to be protected from reality until it breaks through their comfort zone and kicks their ass, as happened to Ukraine after it surrendered its nuclear deterrent for loads of lies on a piece of paper which has now proved no more valuable than worthless paper peace promise which Hitler signed on 30 September '38.
ABOVE: in 1979, the basic data on yield, weight and configuration of various nuclear devices including data on the primary stages Swan (Redwing-Inca, 15.2 kt W45, 11.6 by 22.8 inches, 105 lb; also tested as the primary stage inside the successful 360 kt Redwing-Mohawk thermonuclear test) and Swallow (Redwing-Kickapoo, 1.49 kt, 8 by 28 inches, 225 lb), and megaton range thermonuclear device Bassoon (Mk41 Redwing-Tewa, 5.01 Mt, 87% fission, 39 by 135.5 inches, 15,735 lb; and in its cleaner form Redwing-Zuni, 3.53 Mt, 15% fission, 39 by 135.5 inches, only weighing 12,158 lb due to replacement of U238 with lead, which - contrary to populist myths - is not entirely useless or inert since lead does undergo a beryllium-like (n,2n) reaction for T+D fusion neutrons with energy exceeding 10 MeV, with the (n,2n) lead neutron cross-section reaching 2 barns for 14.1 MeV neutrons), and the use of plastic foams to reflect and channel X-rays for the ablative compression of thermonuclear fusion stages, with tested design results (rated in megatons per metre length of fusion cylindrical stage), was disclosed in report UCRL-4725, Weapon Development During June, 1956. This was after having been mistakenly declassified 4 years earlier, on 30 July 1975. Only 56 copies of this secret report were printed, and the whole report was declassified accidentally when only pages 23-29 should have been released. Bassoon worked like the Mike and Castle devices, which were basically Teller 1946 Classic superbomb cylinders of thermonuclear fuel ignited at one end, but sideways compressed by x-ray ablative compression on the cylindrical surface rather than end-on heating through a beryllium shield as Teller has envisioned in 1946, utilizing a relatively low yield fission primary stage to initiate the thermonuclear burn. Howard Agnew told Richard Rhodes (Dark Sun, 1995) that in the 1952 Mike device, a layer of plastic foam was attached to the lead lining on the inside of the casing of weapons to act as "x-ray mirrors", preventing the ablative blow-off of metal into the radiation channel by x-rays. However, the British designer - Brian Taylor - of the first successful 1.8 megaton spherical secondary stage test in 1957 on TV recently reported that their devices used plastic foams filling the entire x-ray radiation channel, in order to allow isotropic (uniform from all directions) ablation of the pusher around the spherical fusion stage, which would be harder to achieve by x-ray mirrors than was the case for the simpler cylindrical geometry of the fusion stage used by Teller in Mike. According to the June 1967 Sandia Corporation's originally secret thermonuclear weapons development history (extract below), the new Los Alamos Maniac I computer's first task in 1952 was to determine "... the flow of radiation pressure along channels between fission and fusion components of the bomb ..."
Rather than the x-rays simultaneously compressing the whole cylinder (which is what Hansen and Morland show in their illustrations, ignoring the time factor), the thermonuclear burning wave - if the x-rays are slowed down by plastic foam filling the radiation channel - propagates along the cylinder beginning at the end nearest the primary stage: by having a sufficient "spark plug" of fissile material in the core (both to irradiate compressed LiD with neutrons, fissioning some of the lithium into tritium, and also to provide heat to initiate fusion in the compressed fusion fuel), a self-sustaining burning wave could be established, so that you could increase the yield simply by making the cylinder longer (the Bassoon was increased up to 25 megatons in the W41, five times the Tewa test yield!). In such a design, the role of plastic foam blocking the radiation channel, is to deliberately prevent the rather limited primary stage x-ray energy yield from being diluted excessively by flowing over the vast surface of the secondary stage cylinder, which would reduce the compression and lead to secondary stage fizzle. The whole point of the hydrogen bomb is to get away from the critical mass yield-limiting problem of fission weapons, and you can't do that if there is no way to control the spread of the vital x-ray radiation from a primary stage when you have a very large secondary stage to compress. The diagram below applies to the basic W41, but note that the neutron shield between the primary and secondary stage is there to prevent pre-initiation of fission in the core spartplug of the secondary, cylindrical stage, but in a very clean weapon like 95% clean, 5% fission Redwing-Navajo, there is no spark plug so the neutron shield is replaced with a neutron channel to allow primary stage neutrons to fission lithium, producing tritium in the secondary stage, prior to its compression. Furthermore, Bassoon's 15% and 87% fission yield versions showed the effect on both bomb yield and mass of replacing the U238 ablative pusher around the fusion clyinder with lead to make it much cleaner. The results showed that doing this drops the mass from 15,735 to 12,158 lb, while only reducing yield from 5.01 to 3.53 megatons. Moreover, while you get an area of 520 square miles giving a fallout dose over the first 50 hours of 1000 R (survivable indoors with the shielding provided by most city buildings) for the "dirty" version, this drops to only about 150 R for the "cleaner" version, for land equivalent surfaces outdoors. As a result, details of nuclear warhead designs were published in various books and articles. At this point (if not in 1949 with Fuchs, Greenglass and other spies giving Stalin the bomb "for peace"), sensible people realise that "secrecy" markings on documents sooner or later fail to protect you from dictators, so you instead need credible nuclear deterrence and civil defense.
ABOVE: Dr Gregg Spriggs of Lawrence Livermore National Laboratory, who gave Hans Rosenwinkel (producer and director) a PBS America TV interview recently (in the 2021 TV documentary on the Bravo test, called "Burning Sky", first broadcast on PBS America digital channel in the UK on 26 June 2021 after being broadcast 3 days earlier in the USA; we taped it for personal use but due to copyright cannot upload it to youtube), claiming that water spray in most Pacific nuclear tests led to yield underestimates so Bravo would be 22 megatons not 15 megatons, leading - if correct - to even greater reduction in the measured effects of nuclear weapons of given megaton yields shown in Glasstone's book: "They did their best back in the 1950s ... on Bravo they had adjusted the analysis somewhat ... when you do a shot over water, as the shock wave moves out it picks up water and it makes the shock wave heavier, so we think now that the yield of Bravo - and in fact the yield of all of the barge shots that were done in the Pacific - were about 27-50% higher than what was originally reported, so Bravo, instead of being 15 megatons, might actually have been on the order of 22 megatons!" (We're not updating the Pacific nuclear tests yield data on this blog until we see the reports with hard data on this, because the 1950s yields were also substantiated by radiological yield from fission product and actinide samples in fallout, which doesn't depend on shock wave data or fireball expansion films! However, this claim about H-bomb yields in the Pacific being underestimates is interesting, and Dr Spriggs may well have secret-classified reports hidden from public view, with more data which will eventually be declassified and become available. If indeed the total fireball expansion-derived yields are higher, then the percentage fission yields - derived from fallout sample analyses - must be smaller by a similar factor, which would have huge implications for not just nuclear weapons effects but also for constants in the semi-empirical models of nuclear weapon designs for megaton yields!) He has also put some recently restored films of nuclear test explosions on youtube. The most interesting, in view of the photo of the "upright" test configuration of the 5 megaton Redwing-Tewa bomb at Bikini in 1956 (see photos at the top of this blog post for a pic of the Mk41 Tewa test prior to testing) shows the primary stage being ejected vertically upwards out of the fireball and creating a second smaller fireball above the main fireball produced by the main cylindrical secondary stage (which is heavier and nearer to the ground), an effect analogous to that seen in the 1962 Starfish test (basically the two stages are exchanging radiation which causes them to recoil apart as the weapon case vaporizes, and the lighter primary stage gains the most velocity, due to straightforward conservation of momentum):
UPDATE - 6 April 2022:
The roots of the present crisis are covered in General Sir John Hackett, DSO and Bar, MC, LLD, et al., The Third World War, Book Club Associates, 1978. Hackett was an Australian born Oxford classics and history scholar, who went into the British Army when Hitler went off the deep end in 1939, being wounded while leading a parachute brigade against the Nazis at Arnhem. He ended up NATO Commander of the British Army on the Rhine, when he started a political war with the British Government by writing a famous letter in The Times complaining that NATO was under resourced and needed strengthening to resist Russia. He survived that by claiming he was wearing his NATO hat, not his British Army hat, when writing the letter (the British Army bans its employees from writing politics in the press, whereas NATO doesn't). After retirement he became Principal of King's College, London, and then wrote The Third World War to point out the risk of NATO weakness encouraging Russian aggression, just as he had seen happen with the Nazis in the 1930s, stating in Authors' Note and Acknowledgements (p 359):
"Those who argue for the reduction of defence expenditure in the countries of the West .... seem to live in a land of total make-believe ... What they [Russia] have been doing is building up huge armed forces, far greater than what would be necessary, in any conceivable situation, for their own defence, at a cost gravely detrimental to domestic development ... and in a mode essentially offensive. ... We have assumed that enough is done to ensure that, when the Soviet machine travels of its own momentum along a path of miscalculation and mischance towards an attack on NATO, the West, at some cost, is able to survive. It is possible, of course, that enough will not be done. The outcome is then likely to be different. ... the free countries of the West would be in no position to withstand political pressure from the USSR, which would enjoy the fruits of a military victory, without having to fight for it."
Hackett and associates outline what they consider the most probable nature of WWIII, pointing out (on page 31) that in 1978 only 35 out of 180 governments in the world were truly democratic, and the remainder relied on dictatorial succession or coup d' etat for changes of leadership. They assume (Appendix 5, p355) that the West has a nuclear inferiority by 4 August 1985 when they assume WWIII breaks out, with 2450 ICBMs, IRBMs and SLBMs on the Russian/Warsaw Pact side, compared to just 1900 available to the West. They assume that Russian assistance to Egypt causes subversion and overthrow of Middle East countries (Saudi Arabia, Iraq, and Kuwait) in 1984, with Saudi's Sunni sect versus Iraq's Shia sect being provoked by insurgency to cause war. Russia also attacks Western assets, ships etc, leading American hawks to propose (p 282): "Why not now go over to the offensive, it was asked, and finish off forever the threat ... East Germany and Poland could be freed and the advance could be pushed forward in the Ukraine as far as the Dnieper. Control of the Ukrainian harvest and of the Dnieper hydro-electric installations would be enough to cripple any further war effort by Soviet Russia. It would be tempting to go on and liberate Georgia and control Baku, but that ... would expose too long a line of Western communications ..." Instead, the Russian Kremlin followed President Truman's doctrine of 6 August 1945 (p 285): "They insisted on an immediate move towards the threat of nuclear action. A single atomic attack on a Western target would be enough to demonstrate their determination. A simultaneous message would be sent to the US proposing the immediate withdrawl of all foreign forces ... It was important to make it absolutely clear to the Americans that this was a single attack to demonstrate what might happen if they refused Soviet demands. It was not to be seen as an immediate prelude to a general nuclear offensive. ... Most views were fairly near the truth so far as a proposal for negotiation was concerned, but few guessed that this would be accompanied by a Hiroshima-type demonstration, or that the time-table would be as narrow and threatening as it turned out to be ... he demanded that the US should send representatives within one week ... failing which further selective strikes would be carried out."
After the explosion, NATO retaliates with a similarly small-scale tit-for-tat nuclear strike, being constrained by escalation fears (a factor which contrary to CND propaganda, was the prime factor in all NATO Cold War plans). Hackett comments on the Cold War conflict between oppressor Russia and its victim Ukraine (p 306): "Soviet policy had always been at pains either to suppress or appease any symptoms of independence of mind on the part of Ukraine [Khrushchev gave Ukraine the Crimea in 1954]. Its enormous contribution to Soviet food supplies, its position in the front line of Soviet territory facing the West, bordering on Poland, Czechoslovakia, Hungary and Romania, and its vast hydro-electric potential, had made it, after Russia proper, the most vital component of the [Soviet] Union."
Hackett argues (p 311) that Marxism only took root among a "group of people accustomed to absolutism", such as those in the Tsar's Russia of 1917 or Ho Chi Minh's Vietnam, and failed elsewhere, unless continuously enforced by a regime of brutality and violence. Put another war, "Marxism" was essentially successful merely because it became a mere public relations symbol or label, used as a handy excuse for excesses by dictators, just as certain religions were likewise used as mere excuses for invasions labelled Crusades or Holy wars in the past. His conclusion (p 327) is that WWIII would end Cold War Russia's role as a Western superpower, leaving China (largely a rival to Russia in the Cold War) to take its place: "After each major war this century, a great empire has melted away. After the 1914-18 war, the defeated Austro-Hungarian empire. After the 1939-45 war, the victorious British empire." The basic problem remains that relatively few countries are completely democratic and free, while many have military power. The cheap-fix of disarmament for this world is beautifully debunked by world history following the nonsense written on pages 101-2 of the 1931 book by Major Victor Lefebure, Scientific Disarmament (published by the communist Victor Gollancz's Mundanus Ltd imprint in London, with glowing Introductions by 14 disarmament "experts" including David Lloyd George and H. G. Wells): "The claim that a peacefully disposed country, highly organised for industry, with vast facilities for manufacture of all kinds, can suddenly spring from a condition of disarmament to one of intense armament appears to be untenable." (Hitler disproved him soon after being elected two years later. This book was given a lengthy and laudatory review in The Observer on 1 March 1931 by a Major-General Sir F. Maurice!)
Update: 17 April 2022. President Biden is sending further military aid for Ukraine to fight Russia, $800 million including 500 Javelin armour penetrating missiles, two hundred M113 APCs, eleven Mi-17 helicopters, eighteen 155mm howitzers, 40,000 artillery shells, 300 switchblade drones. The problem is that this kind of proxy conventional war can drag on, devastating the country. If you remember the neutron bomb "controversy" from 40 years ago, Reagan's admin argued (1) they'd deter invasions, and (2) if some kind of accidental special military adventure/invasion occurred, then they'd swiftly stop the armour without any collateral blast, fire or fallout damage (1 kiloton enhanced radiation/reduced blast at a few hundred metres doesn't cause any damage apart from a flash of nuclear radiation to stop/deter invasions, UNLIKE conventional weapons which leave the country in ruins and hurt civilians). According to Sandia's declassified Defense Nuclear Agency Nuclear Weapons Characteristics Handbook, pages 13-15: "With the advent of the Korean War in 1950 ... our focus shifted to tactical nuclear weapons. The Mk7 bomb and the Mk9 280mm artillery fired atomic projectile were the first of these weapons. In the early 1950s we started developing nuclear warheads for short-range missiles such as the Honest John and the Corporal ... In 1962, President Kennedy directed that permissive action links (PALs) be incorporated in all NATO deployed weapons to protect against unauthorised use." Deterrence was lost in the 90s due to lying anti-nuclear propaganda disarmament activists. Without credible nuclear deterrence, we are back to long sieges of cities, where attrition in the face of dwindling food and ammunition determines the outcome, as in the 11 month long siege of Sebastopol in Crimea, from October 1854 to September 1855, or its siege from October 1941 to July 1942 (during June 1942 alone, Germany reportedly dropped 20,528 tons or 20.5 kilotons - more than twice the blast yield of the Hiroshima bomb - on Sebastopol, which of course goes unnoticed by the anti-nuclear propagandarists who don't care deterring conventional war).
________________________________
https://www.standard.co.uk/news/world/president-zelensky-putin-russia-ukraine-nuclear-weapons-b994743.html
President Zelensky warns world to prepare for Russian nuclear attack on Ukraine
The Ukraine leader called for more air raid shelters and more anti-radiation medicines
By Sami Quadri, Evening Standard, london
Ukrainian President Volodymyr Zelensky has said the world should be ready for the prospect of Vladimir Putin using nuclear weapons.
Speaking from the country’s capital Kyiv, Mr Zelensky voiced his fears the Russian president could also be prepared to use chemical weapons against Ukraine.
The leader called for more air raid shelters and more anti-radiation medicines.
________________________________
https://www.dailymail.co.uk/news/article-10726663/Increasingly-desperate-Vladimir-Putin-attack-NATO-base-stop-weapons-getting-Ukraine.html
'Increasingly desperate' Vladimir Putin could attack a NATO base to stop the western weapons that are stalling his invasion from getting to Ukrainian forces, ex-national security chief warns
Putin could strike a NATO base in order to halt the transfer of arms to Ukraine
Former Government security adviser Lord Ricketts made the warning yesterday
Putin may even attack aircraft or convoys headed to Ukraine from NATO, he said
By JESSICA WARREN FOR MAILONLINE
PUBLISHED: 19:00, 17 April 2022
Vladimir Putin could consider striking a NATO base in order to halt the transfer of arms to Ukraine, a former British security chief has warned. Lord Ricketts, the Government's first national security adviser, said yesterday that Mr Putin is becoming 'increasingly desperate to choke off the flow of arms' to Ukraine. He may even do this by attacking aircraft or convoys headed to the country from NATO, Lord Ricketts suggested. ... Ukraine's president, Volodymyr Zelensky said that it is important for Russia not to win any territory in the Donbas region. ... 'We shouldn't wait for the moment when Russia decides to use nuclear weapons ... We must prepare for that,' he said.
________________________________
This is the place and time to once more debunk Dr Hans A. Bethe's nonsense anti-Reagan address in April 1982 to the American Physical Society, "We are not inferior to the Soviets" (published on pages 90-98 of Bethe's book The Road from Los Alamos, Touchstone, 1991). Bethe admits in table 1 of his article that the Russian empire had 2,490 ICBMs, SLBMs and bombers, compared to just 2,030 American delivery systems, and also in his table 2 that the nuclear warheads on these systems amounted to 8,000 equivalent megatons on the Russian side, compared to just 5,600 American. However, he then made the totally false propaganda claim that this vastly superior Russian nuclear force "is cancelled by the lower accuracy of their missiles"! This is totally misleading "chalk versus cheese" propaganda fake news from Bethe, because the American and Russian targetting strategies were different: Russia was targetting soft targets with higher yields that don't require high accuracy, whereas America was trying to target Russian Kremlin leaders bunkers and Russian nuclear weapons in their very hard missile silos, not civilian targets, with lower yield nuclear warheads that produce less collateral civilian damage and injury, but that do require high accuracy unlike the Russian targetting strategy, and in fact America FAILED due to errors in its crater sizes predictions, a fact only discovered at the end of the Cold War! They have been trying to rectify it ever since by "converting" old surface burst tested H-bombs into underground earth-penetrator warheads that can overcome the crater predictions errors by penetrating the ground to tens of metres depth to increase the energy coupling into hardened silos and bunkers, but such converted warheads simply haven't been fully system-proof-tested to work due to the atmospheric test ban treaty! In addition, Bethe quotes Brezhnev propaganda speeches, claims falsely that neutron bombs aren't needed to deter invasions since NATO can somehow use anti-tank missiles against a concentrated tank barriage once it starts (a very dangerous gamble, disproved by numerous surprise attacks in history, and also requiring huge conventional forces mobilized at borders that repeat the 1914 world war disaster), and claims falsely that both sids already have "vast overkill capacity", which is simply not true if in a dangerous crisis one side evacuates target cities and takes to shelters before taking declaring war or taking provocative actions, as Britain did when evacuating kids from London before declaring war in 1939!.
Bethe's book The Road from Los Alamos also contains other nonsense that make clear that he is double-talking subjective political drivel that ignores the real issues. For example, in his chapter headed "Meaningless Superiority", on page 87 he states: "There can be no victor in a nuclear war." Nuclear weapons were used in WWII and victory was declared in both European and Pacific theatres. Bethe just adds the word "nuclear" to the anti-war drivel of the 1920s and 1930s post-WWI pseudo-pacifists, who would think of gas bombs as a cheap short-cut for disarmament propaganda to close down discussions of victory, in the manner that nuclear weapons are used for this purpose today. But a war ended by a demonstration high altitude EMP effects shot which causes fewer casualties than a conventional bomb is a "nuclear war" that evidently disproves this, and then you get into the problem of what he means by "victor". You don't necessarily engage in a war to achieve the kind of "victory" Bethe sneers at; you fight to survive as a free society. But from the left-wing political angle, all you need to say is that you believe the weapons will be used in enough quantities, on such targets to make the survivors envy the dead, and bob's your uncle: the debate closes in your favour since nobody wants such an argument. However, did Hitler drop his 12,000 tons of deadly tabun nerve agent (or his smaller sarin nerve agent stockpile) in a knockout blow to win World War II, or did he not? Those weapons were found in 1945 when Germany was invaded, and dumped in the Atlantic. The point is, by distributing gas masks to everybody and shelters to keep the liquid droplets off the skin, the gas bomb threat was discredited. The same applies to simple fallout radiation precautions: anything to keep fallout off the skin stops the beta burns that the Marshallese and Japanese fishermen suffered in March 1954, while simple shelters also shield gamma rays fom fallout, which are of relatively low energy for the Russian designs with U238 casings, where neutron capture produces a lot of low energy gamma rays from Np239 and U237 for the crucial sheltering period of 1-10 days after detonation. Bethe ends his meaningless "Meaningless Superiority" article by declaring on page 89: "Negotiations on arms control must not be linked to 'good behavior' ... We Americans should have learned in Vietnam that we are not the policeman of the world." This is a simply a reversal of the lessons of WWII, it is a retreat to the isolationism of the 1930s, when America followed Britain's stupidity and failed to get involved in actively stopping or credibly deterring Germany and Japan from starting WWII. If anyone wants to draw lessons from the Vietnam war, he should do so using Ambassador to the Soviet Union Foy D. Kohler's analysis of the megatonnage dropped on Vietnam and its failure to win the war due to simple Vietcong shelters and survivalism which completely repudiates strategic bombing, linked here.
Regarding nuclear shelters, Bethe attacks them on page 60, where he admits that if nuclear weapons are used on military targets, "then fallout shelters will be very useful", he then irrationally reverses this in the next sentence by saying that since Russian nuclear weapons are targetted on soft targets (countervalue), not hard silos (counerforce), such an attack is "highly unlikely because it is ineffective against an invulnerable missile force." Bethe knows nothing about the true hardness of the Russian shelter system against all kinds of nuclar attacks, counterforce and countervalue. But his argument against shelters, by claiming Russia has superior deterrence in being able to do countervalue attacks, contradicts his own claim in another chapter of his book, where he claims that Russia's superior equivalent megatonage and missiles stockpile is not superior for deterrence, because it has less accurate missiles. Bethe merely redefines the meaning of "superiority" to whatever suits his subjective political agenda. What are we trying to deter? According to Bethe's Russian inferiority argument, we are trying to deter Russia from damaging our nuclear warheads, which is not a problem because the Russian missiles are inaccurate. But that's not what most people are concerned about, which is deterring Russia from attacking civilians. In that sense, Russia has superiority, because accuracy is not a problem for hitting targets the size of cities (as compared to missile silos or Trident submarines). Accuracy is then irrevelant. But it is also largely irrelevant in any case, since submarines hidden at sea are hard to hit so any "counterforce" strategy against a nuclear trident of mixed forces (planes, submarines hidden at sea, and silos) is half-baked at best, and in any case, Russia had not only vast countervalue superiority, but also counterforce superiority, since it turned out that simplistic Glasstone crater size analysis was false and massively exaggerated, so the nuclear weapons targetted on Russian silos wouldn't have done the job Bethe supposed, even ignoring Russian submarines hidden at sea!.
In yet another deceptive propaganda essay, Bethe's chapter on SDI claims that "to be useful" a Western ABM system or space based defence (Reagan's strategic defence initiative) would have to shoot down "virtually all of the 10,000 or so" Russian weapons! Again, this is Bethe's highly bigoted view of how Russia will use nuclear weapons in WWIII: he thinks they will disarm themselves by firing everything they have to overwhelm a Western ABM or other defence system. This is the 1914 and 1939 "knockout blow" delusion that Kahn debunks. Since they have a protected second strike force, they don't need to do this. The far more likely threat of a rogue missile or limited demonstration attack in the manner of Hiroshima or Starfish Prime, is ignored by Bethe. It isn't ignored by Russia which does have an ABM around Moscow for this reason! Bethe then on page 124 then claims that a high altitude nuclear detonation releasing 1 kev soft X-rays to pump a directed "x-ray laser" (in fact you don't need anything so fancy, since a tube or case around the weapon, with one end open, will function to send out a directed pulse of x-rays, as proved in numerous tests, starting with the x-ray fireball coupled into vacuum tubes in the Bravo test of 1954), is useless because warheads can be protected by "A crushable layer installed under the [missile] skin [which] could prolong and weaken the [x-ray ablative "blow off"] pressure wave ... thereby protecting both the skin an its contents." Again, this is deliberately scientifically vague, because no calculations about the range, yield, cost to the missile in terms of size and payload increase trade-off, etc., are given. Sure, you can harden missiles by making use of the large take up of energy in deformation beyond the elastic limit, which is how Lord Baker's clever design for the Morrison table shelter worked in WWII (as with car crumple zones, denting absorbs energy very efficiently, allowing a 3mm steel sheet to stop a collapsing house, something you can't achieve cheaply if you you design a shelter not to be dented, the classic delusion of green engineers set to work on shelter design). But you can use the 14 Mev highly penetrating neutrons from a neutron bomb to melt the fissile material in an incoming enemy warhead, causing it to fizzle, ending that threat!
(Reagan's controversial SDI nuclear explosion pumped X-ray laser was first suggested in 1977 by Lawrence Livermore's George Chapline Jr. and was tested underground in Nevada in 1978, with the x-ray detector instrument breaking down so no results came. In summer 1979, Chapline held a meeting at Lawrence Livermore lab to design a re-test, where Peter Hagelstein suggested an improvement which led to the successful "Dauphin" sub-20 kt nuclear explosion test of the Excalibur pumped x-ray laser underground Nevada on 14 November 1980. It used laser rods made of doped fogbank like the lowest density x-ray transmitting foams in the W76 warhead, but until it is declassified in full with the test results, it will remain on the sci fi shelves of the library. Hegelstein has one very vague report online about x-ray laser technology, a data-dump list of possibities and a lot of references, but no illustrations or definite schemes.)
According to the declassified American 30 July 1963 "DCI (Director of Central Intelligence) Briefing to the Joint Chiefs of Staff", the Russian nuclear warhead designs up to 1963 below 150 kt all exceeded 600 lb in mass, and adds on page 8 that: "There is no information indicating that the USSR has successfully designed and detonated low yield thermonuclear devices with enhanced radiation and reduced fission or devices with the secondary heavily loaded with oralloy such as the US TUBA device [Tuba was the secondary stage used in the 773 lb, 18" diameter, 46.6" long higher yield Polaris W47-Y2 missile warhead, tested to yield 1.2 megatons in the Dominic-Harlem test dropped from a B52 to detonate with a yield-to-weight ratio of 3.42 kt/kg, at an altitude of 13,645 feet, 17 miles south of Christmas Island on 12 June 1962]. In the case of reduced fission devices the chance of collection and analysis of test debris is markedly reduced for low yield tests and thus the absence of debris analysis indicating the detonation of such devices in the 1961-62 test series cannot be considered conclusive negative evidence." The document also states that Kingfish and Bluegill Triple Prime high altitue tests at altitudes of about 100 and 50 km in 1962 were both 200 kt warheads, not 410 kt as previous data suggested. The diagrams from this very important declassified Top Secret nuclear designs document, which plot a graph of Russian versus American warhead test results (the ratio of yield to mass of bomb, with identified data points for specific Russian and American tested devices including the cleaner "Ripple II", a hollow rippled fusion second stage design by John H. Nuckolls of Livermore lab, which when tested as 7,139 lb Dominic-Housatonic, yielded 10 megatons with alleged 99.9% clean fusion yield on 30 October 1962, superseding the success of previous secondary stages Bassoon, Cello, Fife, Oboe, Calliope and the spherical Tuba) and tabulate a comparison, are of poor quality - hand-drawn not typeset due to the problems of disseminating Top Secret data to printers - but are sufficient to see the key facts (note that this data has NEVER been superseded from the Russian point of view, because this direct data on Russian nuclear weapons from fallout samples ended in 1963 due to the atmospheric nuclear test ban treaty, which moved tests deep underground until they were halted altogether, so since 1963 there has not been fallout analysis data to determine Russian designs):
Tape-recorded White House Meeting on the Dominic Nuclear Test Series, 5 September 1962 (Meeting on the Dominic Nuclear Test Series, 5 September 1962, in Tape 20, Box MTG, President’s Office Files, John F. Kennedy Presidential Library (JFKL), Boston, MA.):
President Kennedy: What about our tests? How would you summarize our tests ... how would they? If they [Russian nuclear warhead designers] were talking about our tests would they dismiss them quite as you dismiss theirs?
U.S. Atomic Energy Commission Chair Dr Glenn Seaborg (Nobel Laureate for discovering plutonium): I think that they would not be able to understand the sophistication of some of the biggest advances we have ...
Unidentified participant: our most advanced idea, namely the Ripple concept, leads to an inherently clean system and maximum efficiency ...
McGeorge Bundy: It may be worth just a moment to explain what that is ... Because that is probably the most important technical development in our own Dominic series.
Carl Kaysen: That’s the sort of breakthrough of the Livermore laboratory.
QUOTATION SOURCE: J. Grams, "Ripple: An Investigation of the World's Most Advanced High-Yield Thermonuclear Weapon Design", Journal of Cold War Studies, v23 (2021), issue 2, pp. 133–161.
"In 1957 I was assigned the task of designing a fusion power plant driven by the explosion of a series of hydrogen bombs in a giant steam-filled hole in granite. Although this approach would eliminate the magnetic confinement system, the scale is very large, and the hydrogen bomb is initiated by a fission explosive. ... The feasibility of very small fusion explosions follows from the fact that the thermonuclear burn rate is proportional to the density of the fusion fuel, and the fact that fusion fuels can be imploded to at least 1000 times normal density. The inertial confinement time is proportional to the characteristic dimension of the exploding system. Therefore, for a sphere, a thousand-fold increase in the density (and burn rate) makes possible a thousand-fold reduction in the radius ... less than 1% of the pellet needs to be ignited, since the radius of the compressed pellet is six times larger than the range of the 3.5-MeV alpha particle arising from the DT reaction. If (1/6)^3 ~ 0.5% of the pellet mass is heated to ignition, this critical-size hot spot will then initiate a burn wave which ignites the remainder of the pellet. For this pellet, the minimum required ignition energy is about 5x10^3 J. After compression, the ignition is also energetically 'free'." ... Because the fusion energy is so much larger than the minimum energy required for compression and ignition, an ablative implosion (which is typically 10%efficient) may be used to achieve both compression and ignition. However, because the velocity required for ignition (of a milligram) is roughly three times the velocity required to compress 1000-fold, the overall efficiency is reduced to 1%. ... The 14-MeV neutrons may be absorbed in several tens of g/cm2 of lithium rich material. Lithium fission and (n,2n) reactions may then be used to regenerate the tritium consumed by the DT burn. The soft x-rays and hot plasma are readily absorbed in the lithium-rich material. ... To meet these coupling requirements with the as yet unknown driver, I proposed in the late 1950s to adapt a powerful thermonuclear weapon concept invented by Edward Teller in the early 1950s. I proposed to "indirectly drive" the ablative implosion with thermal x-rays generated by rapidly injecting energy from the driver beam into a cavity which has high-Z walls and contains a DT pellet coated with a low-Z ablator. Re-radiation of thermal xrays back and forth across the cavity rapidly reduces temperature gradients, and rapid ablation of the pellet surface by the x-rays generates the required implosion pressures while reducing the rate of growth of fluid instabilities. To prevent excessive thermal losses into the cavity wall due to the adverse scaling of the surface to volume ratio as the cavity is made smaller, I decreased the cavity temperature and the average initial density of the imploding capsule. In the early 1980s, the U.S. declassified the use of this "indirect-drive" approach in ICF - and the fact that this approach was used in thermonuclear weapons driven by fission explosions. [Emphasis added] ... A program was conducted by LLNL and LANL to implode ICF capsules in underground nuclear experiments driven by underground nuclear explosions. These experiments have been named 'Halite-Centurion'." (Note that there are good technical reports by Nuckolls with the equations predicting fusion explosion charge efficiency here and here.)
Grams states that the Ripple designer, Lawrence Radiation Laboratory physicist John H. Nuckolls, received authorization from President Kennedy to test the first version of Ripple on 2 July 1962, initially set for 5 days later, 7 July, in the crowded Operation Dominic series (America was trying to test every wild idea it could possibly construct and ship to the Pacific, before signing a cessation of atmospheric tests, and some shots failed to get off the ground in time, most notoriously the Uracca high altitude test which Dr Ogle was desperate to have fired at an altitude of 1,300 km, leading to furious technical arguments between Kennedy, his adviser McGeorge Bundy, and testing organiser Dr Frank H. Shelton, documented bitterly in the three books about the 1962 tests by Dr Shelton, Dr Ogle, and Dr Seaborg, respectively, namely Shelton's Reflections of a Nuclear Weaponeer, Ogle's A Return to Testing, and Seaborg's Kennedy, Khrushchev and the Test Ban, all giving very different perspectives on the subject - when Dr Shelton finally got Uracca ditched, Dr Ogle was so furious he tried to pull out of making any more Los Alamos EMP measurements in the high altitude Fish Bowl series in retaliation). (Uracca was first designed to be 410 kilotons, then due to NASA's fears a spaceman might get a few rads, Ogle sold out to protests and compromised and accepted 200 kilotons, but the spacemen put their lives ahead of national security so then the yield was lowered still further, until it was practically a waste of time, due to the very high burst altitude and the evident failure to obtain any significant x-ray effects data on MIRVs for such an unrealistically low yield.) Nuckolls vividly described the overloading of the computer resource time for nuclear device design studies at that hectic testing time, and the desperate use of punched IBM cards for 1-d calculations and only a few 2-d calculations:
"I was the lead nuclear designer and this [Ripple secondary] was my first nuclear test. Not nearly enough time or computer resources were available. Livermore’s nuclear design experts believed success was impossible. [John] Foster and [Peter] Moulthrop were notable exceptions. I severely constrained the nuclear design to minimize calculations, to use parts that could be rapidly fabricated, and to avoid or overpower failure modes. Nuclear design, engineering, and fabrication were completed in two months. (Today, years would be required.) Invaluable assistance was provided by my sole assistant, Ron Theissen, a technician on assignment from the Computation Department. Several other designers volunteered to assist. Day and night, Ron and I punched IBM cards as inputs for hundreds of one dimensional calculations. Although the device was an extreme design, enough computing time was available for only a few simple two dimensional calculations."
Five days behind the original schedule, the first 9,162 lb 56.2x123" Ripple on 11 July 1962, a B-52 dropped Ripple as the very last ever air-drop of Operation Dominic at Christmas Island in the Pacific, named shot Pamlico - it yielded 3.85 megatons with a 14,330 ft detonation altitude to avoid local fallout, and was watched by Nuckolls from the beach on Christmas island, where the first British thermonuclear weapons had been tested five years earlier (Seaborg's book Kennedy, Khrushchev and the Test Ban explains how the emerging scandal about the fallout contamination of Marshallese in 1950s tests made it difficult to resume testing in the Marshall Islands in 1962, so American testing moved to Christmas Island for Operation Dominic, 1962): "The giant mushroom cloud surged upward and stabilized at an altitude of 80,000 feet. The Soviet spy ship was steaming over the horizon. ... My colleagues were amazed at my beginner’s luck and counseled me “quit while you are ahead.” But, I resonated with the creative optimism of Lawrence and Teller. I had no fear of failure. Foster’s rule was if you don’t fail half the time, you aren’t trying hard enough. His dynamic spirit inspired Livermore. “You can excel! I want to run so fast anything the Soviets build will be obsolete. ... In August and September [1962], Ron and I worked day and night to design an even more radical nuclear device [Ripple II]. We further optimized the [primary stage x-ray] pulse shape [using fogbank interstage x-ray pulse shaping] to achieve practically isentropic fuel compression ["if the flow is very gradually compressed (area decreases) and then gradually expanded (area increases), the flow conditions return to their original values. We say that such a process is reversible. From a consideration of the second law of thermodynamics, a reversible flow maintains a constant value of entropy. Engineers call this type of flow an isentropic flow; a combination of the Greek word "iso" (same) and entropy"]. On October 1, this device was exploded in the “Androscoggin” nuclear test conducted in the Johnston Island area of the Pacific. A small percent of the calculated yield was generated. A fizzle!? Everyone believed I had “snatched defeat from the jaws of victory.”
ABOVE: Dr Frank H. Shelton, Dr Bill Ogle, Dr Herman Hoerlin and others at Johnston Island, celebrating the successful firing of the EMP and ABM effects shot 1.4 megaton Starfish Prime at 400 km altitude, with drinks in paper cups half an hour after the midnight detonation, 9 July 1962.
ABOVE: John H. Nuckolls, inventor of the 99.9 percent clean 10 megaton Ripple II H-bomb, based on eliminating the compression of a heavy pusher, and instead using ablative recoil to isentropically compress the fuel itself to higher density than is possible when a heavy pusher is absorbing energy and being compressed itself. The Androscoggin test consisted of a Kinglet primary and Ripple II secondary, 6,647 lb, 128.5x56.2", with a 15–16 megatons predicted yield, but an actual yield of only 63 kilotons. Kennedy received a request on 12 October to retest Ripple II, while Ripple III was tested as Calamity on 27 October 1962, yielding only 800 kt instead of the predicted 3 megatons. Kennedy authorised the retesting of Nuckoll's Ripple II, which was done with modifications as the Housatonic shot on 30 October 1962, yielding 10 megatons from 7,139 lb, 147.9x56.2", without the use of a lead pusher, with a fusion yield of 99.9%, i.e. 99.9% clean (a vast improvement on the 98% fusion 1961 Russian 50 megatons test), according to the “Report by Commander Joint Task Force Eight,” 4 June 1964, pp. L-B-5-1–2, as cited by Grams. Grams makes it clear from declassified reports quoting Seaborg clearly stating that the 98% clean 50 megaton Russian test in 1961 and other clean Russian shots used a lead pusher, which was an entirely different process to the clean mechanism of Ripple II.
Dr Nuckolls explains that the origin of the successful clean 10 megaton Ripple II nuclear weapon design was actually the effort to develop peaceful fusion energy (which failed with lasers but worked with a very low yield fission primary stage providing x-rays!) in his paper "Contributions to the Genesis and Progress of ICF", pages 1-48 of the 2007 book, Inertial Confinement Nuclear Fusion: A historical Approch by its Pioneers (Edited by Guillermo Velarde and Natividad Santamarfa). Basically, the fusion burn rate is directly proportional to the fuel density, which in turn is of course inversely proportional to the cube of its radius. But the inertial confinement time for fusion to occur is proportional to the radius, so the fusion stage efficiency in a nuclear weapon is the product of the burn rate (i.e., 1/radius^3) and time (i.e., radius), so efficiency ~ radius/(radius^3) ~ 1/radius^2. Therefore, for a given fuel temperature, the total fusion burn, or the efficiency of the fusion stage, is inversely proportional to the square of the compressed radius of the fuel at the time! The radiation loss (cooling by inverse Compton effect) problems that Teller's classic superbombs suffered from can be virtually eliminated by lowering the x-ray energy (temperature) to below 1 KeV, because the radiation losses to the nuclear bomb case are of course proportional to the fourth-power of the radiating temperature:
"I was introduced to Teller's radiation implosion scheme in the summer of 1955 ... As a 24-year-old assistant to Harold Brown, the 26-year-old TN Design Division Leader, I studied nuclear explosives and weapons design code development and use. In 1957, Brown asked me to help evaluate the feasibility of producing commercial electric power by periodically exploding half-megaton yield H-bombs in a one-thousand foot diameter, steam-filled cavity excavated in a mountain. This large-scale ICF scheme was part of Teller's Plowshare program to develop peaceful uses of nuclear explosives. I realized that a few hundred electron volt radiation temperature might suffice to implode and initiate a very small-scale fusion secondary. Radiation losses into a hohlraum wall decrease with more than the fourth power of the radiation temperature. With low radiation temperatures, excessive wall losses can be avoided ... Implosion symmetry is enhanced because the radiant energy absorbed in a thin layer of the high Z walls of the hohlraum is efficiently re-radiated multiple times and has a velocity a thousand times larger than the implosion velocity of a fusion capsule. Energy radiates from hot areas to cooler areas, rapidly equalizing temperatures. Growth rates of fluid instabilities are reduced because kilovolt range thermal radiation from a few hundred eV temperature black body rapidly ablates the unstable interface in low atomic weight materials. ... Distortions and instabilities generated by energy concentration processes located in the driver are effectively decoupled from the spatially separate secondary implosion when the secondary is energized by black body radiation from the driver-heated hohlraum walls. Consequently, radiation coupled drivers and fusion capsules may both be operated near their stability limits to achieve maximum performance. Driving pressures of several hundred megabars and implosion velocities of hundreds of kilometers/second can be generated by ablation with several hundred eV radiation temperatures. At these temperatures, material sound speeds are several hundred kilometers/second, comparable to the implosion velocities required to isentropically compress DT to more than one thousand times liquid density. ... In 1961, my group leader, Peter Moulthrop; nuclear designer Ray Birkett; and I addressed the pusher fluid instability problem by separating the pusher from the ablator ... the fusion energy generated can be 10^4 times larger than the Fermi energy of the compressed DT! The gain can be further increased by igniting a relatively small fraction of the DT mass in a hot spot near the center of spherical convergence. Fusion yields can then be amplified by TN propagation from the hot spot into a much larger mass of DT. ...
"I developed an ablatively driven spherical rocket implosion to compress DT to high densities without use of a pusher. A sustained ablatively driven implosion is made possible by use of a sustained driver input and a suitable ablator. Optimum pulse shapes make possible very high isentropic compression of most of the DT while igniting a central hot spot. The temperature of the hot spot is amplified by adjusting the pulse shape so that a strong shock is generated near zero radius, and by using a hollow target design containing low-density DT gas. ... With near ideal pulse shapes, very high-gain, pusherless, near isentropic, low temperature radiation imploded fusion capsules that ignite propagating bum are feasible. ... Livermore's professional weapons designers regarded my tiny low-cost, high gain ICF target designs as science fiction. We joked about "Nuckolls' Nickel Novels" (referring to my prolific series of classified memos). Without nuclear tests, these radical target designs could not be taken seriously. Fortunately, my efforts were strongly supported by Carl Haussmann, who succeeded Brown as TN Division Leader, and by Foster, who succeeded Brown as Livermore director in early 1960. (Brown was selected by President Kennedy to lead Department of Defense (DOD) Research and Engineering.) ... Livermore was focusing all possible efforts on responding to high yield Soviet atmospheric nuclear tests (including a 57-megaton explosion). ... In April 1962, the U. S. responded to the Soviet tests by launching an intensive nuclear test series. Livermore's advanced warheads achieved a major success in an "Admiral's test" of the Polaris submarine launched ballistic missile. This Polaris weapons system addressed the first strike instability, by creating a secure second strike nuclear force. ...
"In April 1962, a few months before the scheduled end of the atmospheric test series, I proposed a nuclear test of a radical high-yield TN design so fantastic that my colleagues thought it was an April Fool's-day joke. In this radical design, a high-performance TN secondary was imploded with a highly optimized pulse. Foster dispatched me to Washington to support approval of a nuclear test of my scheme. I was accompanied by Roland Herbst, a theoretical physicist and experienced weapons designer. I briefed AEC Chairman Glenn Seaborg, and my former boss, DOD's R and D leader Harold Brown. President Kennedy approved the nuclear test the last experiment in the test series."
Dr Nuckolls' scientific and political viewpoint was disastrous when he eagerly used his position as Director of LLNL (at the end of the Cold War, when the research budget was drying up!) to try to start a speculative pie-in-the-sky peaceful nuclear fusion energy program (leading to a major argument with U.S. Secretary of Energy Watkins in May 1992 when Watkins visited LLNL and demanded nuclear deterrence against proliferation and nuclear terrorism, not peaceful fusion energy!), but Nuckolls' views on deterrence were always sound and he warned clearly against nuclear disarmament scams for "peace":
Nuckolls and Lowell Wood (another LLNL physicist, best known for his secretive work on EMP effects from nuclear explosions and for chairing a controversial EMP commission, which produces reports with the vital technical data we need removed due to secrecy concerns) also wrote an interesting article called "The Development of Nuclear Explosives" (published in the 1988 book Energy in Physics, War and Peace, edited by Wood) stating on page 312: "The development of high-yield weapons was motivated strongly by rising concern in the U.S. Government regarding the potentially unstopable character of Soviet land forces, as the nature of the war machine that had broken Nazi power in the 1943-45 period became clearer in post-war analyses. The basic Soviet doctrine of massing forces and breaking through the enemy front, even at very high costs in men and material, came to be seen as very difficult to counter. However, since it involved concentrating a division into a few square kilometers for its effectiveness, 0.1-1 megaton nuclear explosives used as area (blast + thermal) weapons came to be seen as an effective and affordable response by the defense: a single high-yield weapon costing under a million dollars could neutralize an armored division costing several orders of magnitude more."
Ripple warhead designer Nuckolls with Lowell Wood and others had in 1972 published a paper about the new physics involved, in Nature vol. 239, pp. 139–142, see the illustration below. In simple terms, what Nuckolls does to the Teller-Ulam thermonuclear secondary stage is analogous to what happened in the evolution of primary fission stages: get rid of the thick, dense tamper/pusher surrounding the fuel, to allow the available implosion energy pulse to compress the fuel, and to do at the correct rate to get "isentropic compression", i.e. keeping the shock energy in mechanical work (without the conversion of implosion shock energy into heat energy, which reduces the component of the energy being used for compression). The rate of delivery of X-rays can be controlled by low density plastic foams used as baffles and for delayed re-radiation of soft x-rays. To design the shape in detail, an iterative scheme is used, where a range of basic guesswork possibilities are all simulated in detail on a computer, and the best results are then picked out and used as the basic templates for another range of designs, but honing-in on the most promising shapes, thicknesses, etc. This process is repeated many times to optimise a final design, before a nuclear test is done to check that it actually works as intended.
The controlled higher compression factor you get without having to also compress an inert, thick dense pusher (you just use a relatively thin, say 1-cm thick beryllium ablator surface shell) allows efficient, isentropic compression, of a hollow lithium deuteride sphere with D + T gas in the centre to act as an initiator, providing neutrons to kickstart the fission of lithium in the lithium deuteride fuel, replacing the Teller-Ulam fissile sparkplug; something only possible due to the much greater compression in Nuckolls design than in the older Teller-Ulam system.
If you think this is questionable and don't want to believe in a 99.9% clean H-bomb, note that Nature published this paper suggesting that a laser system could be used, in place of the x-ray pulse from a 10 kiloton fission primary stage that Nuckolls used in all of his 1962 tests, and which is way more powerful than laser pulses! There is also an article, "Energy Balance in Fusion Hohlraums", in the unclassified Los Alamos Nuclear Weapons Journal, issue 2, 2009, pages 6-11, which contains two diagrams side-by-side, comparing the use of laser beams and x-rays, such as from nuclear fission primary stages, for focussed x-ray compression of fusion capsules, including a detailed description of the fogbank x-ray mirror lining needed to focus soft, 0.2 keV, x-rays isotropically on to the fuel capsule, and including x-ray shadowgraphs of implosions showing the shockwaves with and without fogbanks/x-ray mirrors which are composed of "20-mg/cm^3 silica aerogel" - the same issue has a helpful article about the use of fogbank interstage material in W76 warheads:
"... Fogbank is an essential material in the W76 warhead. During the mid-1990s, Fogbank production ceased ... As time passed, the precise techniques used to manufacture Fogbank were forgotten. ... Los Alamos computer simulations at that time were not sophisticated enough to determine conclusively that an alternate material would function as effectively as Fogbank. ... Despite efforts to ensure the new facility was equivalent to the original one, the resultant equipment and processing methods failed to produce equivalent Fogbank. ... in some cases the current impurity levels were much lower than historical values. Typically, lower impurity levels lead to better product quality. For Fogbank, however, the presence of a specific impurity is essential. ... . Scientists found that modern cleaning processes, used in the manufacture of the feed material, clean it better than the historical processes; the improved cleaning removes an essential chemical. ... The historical Fogbank production process was unknowingly based on this essential chemical being present in the feed material. As a result, only a maximum concentration was established for the chemical and the resulting impurity. Now the chemical is added separately, and the impurity concentration and Fogbank morphology are managed. ... Just as modern scientists unraveled the secrets behind the production of the Japanese katana [samurai sword], materials scientists managed to remanufacture Fogbank so that modern methods can be used to control its required characteristics. As a result, Fogbank will continue to play its critical role in the refurbished W76 warhead."
ABOVE: the transmission of soft x-rays inside nuclear weapon through the absorbing K-shell electron barrier of aluminium plasma generated by the ablation of an aluminium fusion capsule pusher (aluminium in this example is a plasma at a density of 14 grams/litre and at a temperature of 500,000 K), Figure 6 in the officially (Atomic Weapons Establishment, Aldermaston) approved UK Goverment paper, "Science of nuclear warheads" by Keith O’Nions, Robin Pitman and Clive Marsh, Nature, v415, 21 Feb 2002, pp. 853-857: "Little has been published about nuclear warhead science. Here we set out elements of the programme that will underpin future assessments of the safety and performance of Britain’s warheads in compliance with treaty obligations. ... The approach builds upon previous nuclear test experience and seeks to replace the requirements for further empirical test data by developing a deeper theoretical and experimental understanding of the relevant fundamental science. This must then be drawn together and applied to the nuclear warhead system using intensive numerical modelling. ... Lasers and pulsed power machines are able to achieve relevant densities and temperatures and also produce the only source of data on X-radiation flows. ... In the very hot matter of a nuclear warhead, thermal radiation is particularly important. The crucial parameter is the radiative opacity, which quantifies how thermal radiation interacts with matter by absorption, emission and scattering. It is sensitive to the composition, temperature and density of the material and expresses the degree to which a material impedes radiation flow. ... [Figure 6] The subject material is heated indirectly using a foil radiator or hohlraum, and allowed to expand against a plastic tamper. ... Figure 6 describes the techniques used and shows a comparison of an aluminium opacity experiment with the corresponding calculations. ... As well as opacity and radiation flow, laser experiments can be designed to test theoretical models of complex radiation/hydrodynamic phenomena (Fig. 7). ... [Figure 7] Here a laser is used to heat a ... hohlraum, which in turn heats a piece of aluminium (shown in blue). The resulting jet of aluminium penetrates a piece of polystyrene, which is radiographed by an X-ray backlighter also driven by the laser. The results from two numerical codes are shown together with the X-ray record from the experiment. Both codes reproduce the main features of the flow but show different development of the jet tip. Analysis of the detail will indicate where the theory and algorithms must be improved."
Our point in emphasising the 99.9% clean (fusion) 10 megaton Ripple II bomb, air dropped successfully in 1962, is to demonstrate that the technology and science does exist to make even large nuclear weapons a credible deterrent without any fallout collateral damage. Although the neutron effects from 10 megaton bombs in sea level air are usually severely curtailed by neutron scattering in nitrogen, this can be prevented by using two such devices burst 5-20 seconds apart in time, so that the neutron burst from the second device undergoes hydrodynamic enhancement in the large hemisphere of low-density air behind the shock front created by the first burst, tailored to cover the desired area (the precise time between the two detonations is the control determining the radius of efficient hydrodynamic enhancement of the neutrons from the second detonation). So there are excellent prospects for making the neutron bomb credible as a deterrent against invasions, air burst near borders at an altitude that prevents fallout and blast/thermal collateral damage but deters military field equipment and personnel from invasions.
UPDATE (30 April 2022): https://www.dailymail.co.uk/news/article-10766541/Ben-Wallace-predicts-Russia-use-parade-9-announce-mass-mobilisation-population.html:
"Putin 'could declare war on the world's Nazis' on Victory Day (9 May 2022): UK predicts Russia will use parade on 9 May to announce mass mobilisation of reserves for final push in Ukraine to defeat West's support for Kyiv ... Britain's Defence Secretary Ben Wallace has predicted that Putin may instead use the parade to declare war on the world's 'Nazis' and mobilise his reserves ... Earlier this week, Putin vowed to use nuclear weapons against any country that dares to 'interfere' with Russia's war in Ukraine."
A couple of points about this prediction: (1) Russia has at least 2 million reserves, which would boost the total Russian armed forces to 3 million (the 1 million normal Russian military includes a 1 year conscription of personnel aged 18–27); (2) this would be a major step up what Herman Kahn called the "escalation ladder". To give some kind of context to the threat a Russian military of 3,000,000 presents us with, please remember that as we stated earlier in this post (above): "When on 8 December 1991, the presidents of Russia, Belarus, and Ukraine dissolved the USSR, the Soviet military was 3.7 million strong. "From 1945 to 1948, the Soviet Armed Forces were reduced from about 11.3 million to about 2.8 million men", while the Soviet Union actually increased in size, as puppet governments were installed across half of Europe, despite the American nuclear weapons monopoly until 1949."
ABOVE: Russian state TV Channel One's 60 Minutes show reportedly broadcast the missile trajectories Russia could use and the delivery times to hit London, Paris and Berlin (202, 200 and 106 seconds, for nuclear missiles fired from Kaliningrad). This is because Russia has been left with the world's largest nuclear stockpile of countervalue (city destroying) low-accuracy missiles but high-yield warheads. Such weapons can also be used for high altitude large area EMP strikes, where missile accuracy is again largely irrelevant as it is for large city targets. Until the crater exaggerations farce was exposed firmly around 1988, we had - on paper but not in reality - strategic and tactical counterforce superiority due to the fact that our missiles were so much more accurate than Russian ones, we could hit their missile in their silos (provided we attacked first, before the Russian missiles were launched), and we also had tactical nuclear weapons to deter invasions, which was a credible deterrent to Russian aggression. After 1988, however, the Glasstone and Dolan cratering scam was exposed for what it was, debunking our strategic counterforce deterrent (which was never much good against enemy subs hidden at sea anyway), and then the anti-nuclear "peacemakers" persuaded politicians to disarm our tactical counterforce nuclear weapons, leaving us without a credible deterrent to stop invasions. In the 1962 Cuban missiles crisis, Kennedy had clear nuclear superiority and was able to use that in his TV speech on 22 October 1962 to persuade Khrushchev to back down (he said that a single nuclear missile launched from Cuba, even by accident, against a Western target, would be met by a "full" retalitory nuclear response), but today Kennedy's gunboat diplomacy option has a much higher risk because we have surrendered in the nuclear arms race and Russia is way ahead. And it's nut just Mr Putin. China and North Korea have tested thermonuclear weapons and North Korea's Leader Kim Jong Un recently stated in Pyongyang that it would use nuclear deterrence against "escalating nuclear threats from hostile forces". In other words, the dictatorships are now using nuclear deterrence against us to prevent our interventions for peace, just as Hitler did when he built the Luftwaffe: "Margarita Simonyan, editor of state broadcaster RT and one of the Kremlin's highest-profile mouthpieces, declared on TV last night that the idea of Putin pressing the red button is 'more probable' than the idea that he will allow Russia to lose the war. 'Either we lose in Ukraine,' she said, 'or the Third World War starts. I think World War Three is more realistic, knowing us, knowing our leader'." - https://www.dailymail.co.uk/news/article-10762143/Ukraine-war-Russian-state-TV-says-nuclear-strike-probable-losing.html
UPDATE: https://www.dailymail.co.uk/news/article-10774235/Ukraine-war-Russian-state-media-threatens-UK-underwater-nuke.html: "Russia's chief propagandist threatens to 'plunge Britain into the depths of the sea' with underwater Poseidon nuke that would trigger a 1,600ft radioactive tidal wave and wipe the UK off the map. Dmitry Kiselyov, known as 'Putin's mouthpiece', threatened the UK with Poseidon underwater nuclear bomb. By CHRIS PLEASANCE and WILL STEWART FOR MAILONLINE. PUBLISHED: 08:36, 2 May 2022 | UPDATED: 13:21, 2 May 2022. Dmitry Kiselyov, a man often known as 'Putin's mouthpiece', used his Sunday night show to call for attacks on Britain with a Poseidon underwater drone that he said would trigger a 1,600ft radioactive tidal wave and 'plunge Britain to the depths of the ocean.' The drone 'has capacity for a warhead of up to 100 megatons', Kiselyov claimed - several thousand times the strength of the bomb dropped on Hiroshima - which would 'raise a giant wave, a tsunami, up to 1,640ft high' - enough to reach halfway up Scafell Pike, the tallest point in England. Speaking against a background graphic showing the UK being erased from the world map, Kiselyov added: 'This tidal wave is also a carrier of extremely high doses of radiation. Surging over Britain, it will turn whatever is left of them into radioactive desert, unusable for anything. How do you like this prospect?'"
There is now detailed published data on the Russian underwater nuclear tests: see Vice Admiral E. A. Shitikov's paper, Testing ships at the Novaya Zemlya test site (see illustrations of the ship set ups for the 1955 and 1957 underwater tests, below): "On Novaya Zemlya, three large-scale full-scale experiments were carried out to study the effect of the damaging factors of an atomic explosion on ships. ... First experience, September 21, 1955 ... to test the atomic charge for a 533 mm torpedo, to assess the impact of an underwater nuclear explosion on ships, and to obtain experimental data to develop the theory of an underwater nuclear explosion ... in Chernaya Bay at the Novaya Zemlya test site, September 21, 1955, power 3.5 Kt, depth 12 m. In the center of the battlefield was a small minesweeper T-393 project 253l, from which a torpedo with a charge was lowered on a cable to a depth of 12 meters. This operation was led by Lieutenant Commander E.L. Peshkur. Target ships were installed at six radii from 300 to 3000 meters. Surface ships stood side and bow to the center of the explosion, submarines - in the surface and underwater position at periscope depth. ... S-19 - due to the fact that the cork on the torpedo tube was knocked out (in accordance with the test program, the front cover was open) , about 15 tons of water entered the first compartment (the damage was repaired by personnel in two days). ... the sinking radii amounted to 300-400 meters, significant damage to light surface ships occurred from a shock wave at a distance of 500-600 meters. Damage to the superstructures of light surface ships from an air shock wave - at a distance of 700-800 meters. Insignificant damage - at a distance of 1200-1300 meters. ... Immediately after testing B.V. Zamyshlyaev promptly carried out a study in which, in particular, he showed that when the same charge is buried by 70 meters, instead of 12 in the experiment, the effect increases by about one and a half times (in deep water)." There is a lot more to follow, but it is probably best organised into a book rather than blogged about...
ABOVE (update on 13 May 2022): 100% clean H-bomb design (cartoon style sketch, not design blueprint). The basic ideas are illustrated in a previous blog post from 2016, linked here, which describes also the use of von Neumann-Fuchs invention (28 May 1946 patent "Method and apparatus for releasing nuclear energy"of a beryllium oxide ablator as the compressive mechanism in the wall of a fusion capsule. It's clear that the use of plastic and various ablative fusion stage capsule walls underwent a lot of evolution even in the 1950s. That 2016 blog post also gives the references to Teller's idea of magnetic compression of the secondary stage in nuclear weapons, and John S. Foster's work on magnetic flux compression conventional systems to try to power that (however, as we explain, a small nuclear primary stage might be the only way to get it to go!). Another application of such technology is Project orion, a nuclear impulsive drive that is actually practical, tested technology for space exploration which Joseph Friedlander has summarised from blog posts here on The Next Big Future (note that the accidental declassification of the secrets of plastic foam filling the radiation channel of the Mk41 Basoon nuclear device - contrary to its use as a radiation mirror to delay outer case metal ablation in earlier "sausage" devices tested at operations Ivy and Castle, and the Swift, Swallow and Swan primary stage tests in secret UCRL 4725, dated June 1956, originated from the incorrect implementation of a decision to declassify only a 6-pages section in UCRL-4725 about nuclear explosives for propulsion of nuclear rockets for space exploration!).
ABOVE: Zeldovich and Sakharov's January 14, 1954 report, On the use of the product for the purpose of compressing the superproduct RDS-6s which suggested using x-rays reflected by a suitably shaped radiation case on to a spherical fusion secondary stage (a simplified Teller "Alarm Clock", with fissile material in the centre to release neutrons when compressed, lithium deuteride around it which would be hit by neutrons from the fissile material when compressed to fission lithium to yield tritium, an outer shell of uranium-238 as a "pusher" and final fission stage since the 14 MeV neutrons from D+T fusion can fission U-238 efficiently). However, Yuri Trutnev improved this design by placing light material such as beryllium oxide (used as the D+T compressor in the Fuchs-von Neumann superbomb patent) or indeed any light elements (such as the carbon and oxygen in plastics), around the the lithium deuteride. Photo shows President Putin meeting the designer of later successful Russian devices, Yuri Trutnev (then 90), on 15 November 2017. Trutnev says that the 22 November 1955 successful Russian 1.6 megaton thermonuclear test went to Zeldovich's head and he later had a run of three failed bomb designs in a row, before Trutnev was permitted to test his own new design ion 23 February 1958 in the arctic, with great success (860 kilotons air burst at 3 km altitude); the Russians at this time started testing cylindrical secondary stages in an effort to make warheads more compact for ICBMs and SLBMs. Photos of the first AWRE British single warhead for a Polaris SLBM show it to have a tapering secondary stage (an innovation first revealed by Howard Morland in 1979, see illustration below, which also highlights the problem that Los Alamos expert Vernon Kendrick told Morland at Los Alamos in November 1978 that modern warheads "don't use spark plugs [which Kendrick pointed out to be spheres of plutonium throughout the secondary, a 1960s development] anymore" because the fissile oralloy pusher does the job of releasing neutrons to fission lithium into tritium, formerly done by spark plugs, but Morland still included a 1950's style cylindrical spark plug in his diagram of a modern 300 kt MIRV warhead and failed to show the tapering of the outercase in line with the tapering of the secondary), whereas photos of otherwise very similar Russian SLBM warheads first deployed in 1978 show no tapering of the secondary stage cylinder. Russia adopted cylindrical secondary stages in place of spherical secondaries, to reduce the diameter of thermonuclear warhead to fit missiles because it was using x-ray mirroring by the outer casing which makes the weapon bulkier than the American designs; whereas America after 1956 filled the radiation channel with a baffle of low density plastic foam instead of using case mirroring, and so went in exactly the opposite direction to the Russians (America went from cylindrical to spherical secondaries for smaller thermonuclear warheads, whereas Russia did the reverse because it was still using the outer casing as an x-ray mirror and needed more space for the mirroring geometry). Putin is seen presenting Trutnev with the Order of Merit to the Fatherland, First Class.
Update (16 May 2022): https://www.politico.com/news/magazine/2022/05/16/scenarios-putin-nukes-00032505: By GREGG HERKEN, AVNER COHEN and GEORGE M. MOORE, 05/16/2022 12:00 PM EDT. "Scenario 1: Remote atmospheric test. Least provocative would be Putin’s resumption of above-ground nuclear testing — by detonating a low-yield nuclear warhead high ... Scenario 2: Atmospheric detonation above Ukraine. A more provocative demonstration would be an ultra-high-altitude explosion of a more powerful weapon over Ukraine itself. In a 1962 test, the U.S. detonated a 1.4-megaton H-bomb in the mid-Pacific, 250 miles above the Earth. The resulting electromagnetic pulse unexpectedly knocked out streetlights and disrupted telephone service in Hawaii... Scenario 3: Ground explosion in Ukraine. Most dangerous — and, for that reason, perhaps least likely — would be using a tactical nuclear weapon to achieve a concrete military objective such as disrupting the delivery of weapons to Ukrainians... In May 1945, weeks before the successful test of the first atomic bomb in New Mexico, former President Harry Truman’s advisers considered, briefly, the option of a harmless but spectacular demonstration of the revolutionary new weapon as an alternative to its military use, in hopes of compelling Japan to surrender. For practical reasons — there were too few bombs in the U.S. nuclear arsenal, and some feared a dud — the demonstration option was never presented to Truman. But the warning shot idea would surface again and be taken more seriously. During the 1961 Berlin crisis, former President John Kennedy was presented with the option of firing a nuclear-tipped missile at Novaya Zemlya to show American resolve. Israel has also considered a nuclear demonstration; prior to the Six-Day War, in May 1967, Shimon Peres proposed detonating a nuclear device over the Sinai desert to head off the conflict. Six years later, the Israelis again briefly entertained the notion of a high-altitude nuclear warning shot to force an end to 1973’s Yom Kippur War. In 1981, with the Cold War again heating up, Secretary of State Alexander Haig — a former NATO supreme allied commander — let slip that “there are contingency plans in the NATO doctrine to fire a nuclear weapon for demonstrative purposes...” regardless of what Putin decides, engaging Russian forces in direct combat should only be a last resort."
UPDATE (24 May 2022) on yield of Bravo nuclear test: it was mentioned (above) that nuclear effects researcher Dr Gregory Spriggs of Lawrence Livermore National Laboratory, who has been scanning by computer and re-analyzing old films of nuclear test fireballs, went on TV last year (during a documentary about the Bravo test) to argue that due to water entrainment by the fireball affecting the fireball expansion rate, its total yield may have been 22 megatons, not 15 megatons as extrapolated from fireballs over land in Nevada. There are some LLNL reports now available, giving some of the basic data on fireball expansion rates and blast arrival times, that backs up what he said (though for other Pacific tests like Zuni and Dakota, not Bravo - note that I would love to see all the fireball films of Bravo in high definition taken from surface level, rather than aircraft above the clouds, since the rather grainy declassified ones so far available show that normal clouds obscured most of the fireball and its thermal pulse at the surface and that you can also see a secondary fireball running down the diagnostic x-ray vacuum pipes!). I'm particularly interested in this because I did an analysis of the G. I. Taylor fireball expansion formula (on vixra) giving analytical - rather than taylor's shoddy numerical integration ("cheating" according to maths professor!) proof of the correct formula (Taylor didn't even get his numerical integration right, making errors in his derivation; so much for the wonders of his so-called brilliant mathematicial brain!). The new LLNL papers are by Kelly M. Cook, Shockwave Arrival Times from Operation Redwing and Operation Upshot-Knothole, LLNL-TR-814172, which in table 1 shows that Redwing-Zuni whose fireball was partly over an island in the south of Bikini Atoll but also extended over the sorrounding lagoon water to the north and ocan to the south, had an entrainment coefficient of 1.075. The value is 1 for no entrainment like the Nevada Climax air burst, and the yield is proportional to the cube of the coefficient, i.e. 1.075^3 = 1.242, so megaton range tests over ocean would have a fireball yield at least 24% higher (or more than 24% if the area covered by highest overpressures had a larger ratio of water area to land area). Secondly, a paper by Adele Myers, Water Entrainment in Nuclear Detonations, LLNL-TR-758735 (extracts below) shows how a funnel of water enters the surface burst fireball in a comparable way to the funnel of water thrown up by the Baker underwater test as also shown below, thus cooling the top portion of the fireball (which as Stanbury pointed out in his paper cited above is the only part that most city windows can see; relevant to coastal cities or cities around large river estuaries). She also gives graphs of relevant data and notes that this effect has a 100 kiloton yield threshold. Very interesting!
ABOVE: clearly some of these RUSSIAN published fireball photos of USSR tests are carelessly switched over and wrongly labelled, e.g. the 400 kt 1953 and 1.6 Mt 1955 tests are a little similar, and easily muddled up by officials in the photo archives. It will be left as an exercise for the reader to sort them properly! (There are so many similar nuclear test photos of fireballs and mushroom clouds that you get nuclear brain paralysis if you look at too many!) .... But it should be noted that confusions like this also led to errors in Dr Frank H. Shelton's Reflections of a Nuclear Weaponeer (2nd ed, 1990; it is identified by extra pages inserted in places with a letter after the page number), for example he reprints the same photo of 1953 shot Grable twice, once labelled as Grable, and later in the chapter on Operation Plumbbob, labelled as 1957 Priscilla! (Contrary to Dr Cary Sublette's false assertions, sorting Grable from Priscilla photos is very easily identifiable since there was NO SMOKE SCREEN in the Priscilla test, see photo of Grable with black-and-white smoke screen clouds BELOW):
ABOVE: Ukraine's President Zelensky explaining to John Simpson how his call for Putin to be stopped from starting WWIII has been perverted by US media liars who love Putin, and how Putin is preparing Russia for nuclear war (although he has not yet completely prepared; Putin probably requires collaboration with China, North Korea, Iran et al. to defeat the West in WWIII, and fortunately they are not yet ready to go that far according to Zelensky). As a step forward for peace and humanity, we've set up twitter.com/nukegate to fight US warmongers! The current world situation is akin to a repeat of the 1930s, with the West causing war NOT by "appeasement" (the scapegoat lie of the pseudo "historians", regardless of whether they are "for" or "against" appeasement, a total irrelevance and red-herring) but by DISARMAMENT OF THE MOST VITAL DETERRENT CAPABILITIES WE HAD IN THE NAME OF PSEUDO-PEACE DUE TO WEAPONS EFFECTS LIARS BEING ALLOWED TO GO UNOPPOSED IN THEIR SCARE MONGERING BS FOR YEARS, TO REDUCE THE CREDIBILITY OF DETERRENCE, AND THUS TO CAUSE ANOTHER WORLD WAR, as we can see from the following quotation from Marshall of the Royal Air Force Sir John Slessor, GCB, DSO, MC, The Central Blue: Recollections and Reflections (Cassell, London, 1956, page numbers of quotes are given in [square brackets]):
"[p54:] The aeroplane and the bomb enabled us for the first time to enforce submission upon people without killing them. ... [p145:] Where, therefore, blame is due, I must accept my share of it. ... my theme in this chapter can perhaps best be summarized in Sir Winston Churchill's words, 'no foreign policy can have validity if there is no adequate force behind it...' [Slessor is quoting Churchill, Gathering Storm, 4th ed, p337] ... The climax of misjudgement ... was the surrender at Munich in September 1938. ... Sir Winston Churchill remains convinced that it would have been better, in all the circumstances at the time, to fight Hitler in 1938 [note that the 1938 annexation of Sudetenland including Bohemia gave the Nazis the Joachimsthal uranium mine and many other vital war minerals and heavy industries for munitions production, enabling not just Nazi nuclear research but also conventional weapons production which helped sustain the Nazis in WWII, so the 30 September 1938 surrender to Nazi aggression in Sudetenland by Britain was not "just" about a "few Jews in a faraway land" being murdered in cold blood, or whatever Chamberlain claimed, but it was doing the OPPOSITE of "buying time for BRITISH disarmament"; Chamberlain was knowledgably and dishonestly NOT MERELY BUYING TIME FOR ENEMY REARMAMENT (he rearmed Britain more slowly than the Nazis), but he was also PROVIDING RESOURCES FOR NAZI REARMAMENT, a fact omitted in scam "history" books praising the fascist, anti-libertarian, Nazi collaborator and traitor Chamberlain and his toady pals in the British press] ... He himself has written in his book of the overriding influence of the hatred of war in the hearts of the Democracies, and of our national unwillingness to provide the force to back our policy. ...
[p148:] [French army commander at the outbreak of WWII, General Maurice] Gamelin was a likable person, a courtly and confident old soldier; but I thought him then [at the September 1938 meeting between Gamelin and Slessor in London, due to the Munich crisis] as remote from reality as he afterwards proved ... At this meeting, he said he would like to attack [Hitler] on land at once, but that the French were very interested in avoiding air attack, and wanted some days to get their Air Raid Precaution [ARP] arrangements under way (actually they had no ARP worthy of the name). ... He thought that heavy air attacks on England would be difficult - it was possible, but he did not regard it as very important. ... No one can say what would have happened if war had come in September 1938. The real key to the situation was not Poland, as Gamelin thought, but Russia. ... If Russia had intervened loyally and wholeheartedly against Hitler, the whole history of the past fifteen years would have been entirely different. ... [p150:] One fact which it is essential for anyone to realise who wishes to understand ... is that the war of 1939-1945 was the first air war. In 1914 to 1918 the Air had been in its too early infancy to have any very significant effect. ... we really did not know anything about air warfare on a major scale. ... [p151:] Anyway, in those years immediately before the war the possibility of what was referred to as the 'knock-out blow' bore heavily on the minds of the Air Staff. We were faced with a potential enemy who could bring against us something between 1,200 and 1,500 first-line bombers [with a combined blast and incendiary effects power in a single air raid, when correcting for correct nuclear blast and thermal devastation area scaling laws even ignoring the possibility of gas bombing, equal to a typical MIRVed nuclear missile today]. ... There is, of course, always a tendency, which should sometimes be discounted, for Military Staffs to over-insure and assume the worst case. But it is difficult to blame the Air Staff for assuming that we might find the whole air-power of Germany directed against this country very early in a war. That was not impossible ... The Joint Planning Committee, in a comprehensive review of the air defence problem in late 1936, had estimated that we might have to endure prolonged attack on the scale of 400 tons a day - and that scale increased with the growth of the German striking force. ..."
"[p152:] In a minute to the Secretary of State in April 1938, the C.A.S. [Chief of the Air Staff] wrote- 'I feel strongly that the time for mincing words is past and that the Air Staff should state their view of the situation plainly. Their view is that unless the Cabinet are prepared to incur at the very least the full expenditure required for Scheme L and possibly more, we must accept a position of permanent inferiority to Germany in the air. ... in the event of war, our financial and economic strength, which the present financial limitations are designed to secure, will be of no use because we shall not survive the knock-out blow'."
"[pp.160-1:] Looking back at it now in the atmosphere of 1953, it is almost impossible to believe the extent to which financial considerations were allowed to exert such an influence in bringling us to the very lip of disaster in the face of the Nazi menace, in the years immediately preceding Hitler's war. Every undergraduate knows that a sound economic situation is an essential basis of military strength; but that principle was carried to ludicrous extremes under Mr Chamberlain's Government. I remember one of the Chiefs of Staff saying in this connexion that, as far as he could see, a certain Cabinet Minister was primarily concerned to ensure that we had enough money left to pay the indemnity after losing the war; naughty, no doubt, but that is uncommonly like what it seemed to us in those days. ... Even in the full knowledge of facts such as those I have just described, the Government continued to rule early in 1938 that the three fighting Services between them should not be allowed to spend more than about £1600 millions over the five years 1937 to 1941 - an average of little over £300 millions a year for all three Services; and this eighteen months after the Prime Minister [Chamberlain], as Chancellor of the Exchequer, had confirmed that he knew the Germans were spending £1000 millions a year on warlike preparations, a figure which by now, of course, was being greatly exceeded."
"[p163:] The parity idea first became theoretically the basis of Government policy in 1923 at the inception of the old 52 squadrons programme, which followed the post-war period when Britain virtually disarmed herself in the air. ... [p165:] Either we were dealing with Hitler - a mad dog out for blood - in which case ... there should have been no question of parity, or anything else but to outbuild him and kill him, regardless of any other consideration; it would have been cheap at the price. Or we were dealing with a German Government ... We should have recognised what we were up against when Austria was swallowed up - at the latest. ... we did not really get down to arming ourselves on the necessary scale and tempo until after the fall of France in 1940. ..."
"[pp.169-170:] So a time comes, when war appears really imminent, when the 'shop-window' policy [e.g., lying propaganda fed from the prime minister to the editor of the Times to print rubbish on the front page like, a single gas bombing raid or nuclear firecracket can wipe out a city so we don't need to spend serious money on deterrence of yet another world war] must go by the board. This time, in our view, was overdue when Hitler absorbed Austria. On the morning when the German columns were moving on Vienna (March 12, 1938), I sent a minute to the C.A.S. ... 'You may think it wise to suggest to the Secretary of State that ... we should now base our arrangements on the assumption that we may be forced into war this summer'."
Regarding Winston Churchill, a wartime friend of Slessor whose rantings about the Nazis were ignored by Chamberlain and his entourage partly (as we explained previously on this blog) because Churchill was the last person to be able to lecture them (he sent most of them to hell in his disastrous Gallipoli campaign of 1915, which led to his being fired from the Cabinet in WWI and then being deemed a "warmonger" and fool in the 1930s when he warned those men he had sent to hell in what sounded to them like a conceited, deluded, vain war-mongering prophecy), Slessor writes on pages 259-260:
"But I do not regard uncritical adulation as a compliment to any man. Mr Churchill is human, and as such makes mistakes; and the mistakes of a really big man are liable sometimes to be big mistakes. I am not so arrogant as to claim that when I disagreed with him I was necessarily right. But this book aims to be a humble contribution to history by recording events as they appeared ... I confess that I thought at the time, and still think, that policy in Scandinavia in the opening months of 1940 was one direction in which Mr Churchill's splendid aggressive spirit got the better of his judgement. ... On September 20, 1939, in the House of Commons, Mr Chamberlain said, 'What we will not do is to rush into adventures that offer little prospect of success and are calculated to impair our resources and to postpone ultimate victory ... Strategy is the art of concentrating decisive force, at the decisive point, at the decisive moment'. That perfectly sound principle had not prevented the British Government a few days before from issuing a declaration that a German attack upon Norway would meet with the same resistance as an attack upon Great Britain; a declaration, unexceptionable in theory, to which we had about as much chance of giving practical effect as to our earlier guarantee to Poland of all assistance in our power - which amounted to precisely nil."
Naugthy, but true. Chamberlain, the lover of Nazism, was the better strategist, whereas the more "experienced" military man, Churchill was a bungler competent only to issue ranting Goebbels' style propaganda, aided by brandy and cigars, who needed constant restraining and coercing by the straight-jacket of his asylum keepers like Slessor, who were often overcome by Churchill's fits of insanity. In reality, Slessor writes on page 258, Churchill was a baby who was most happy playing his war with toy bombs:
"This [fluvial mine prototype] was really a sort of toy that Mr Churchill enjoyed playing with - a toy with just the appropriate flavour of aggressive villainy. I remember him one evening, as the little gadget in the fire-bucket touched off its electric bulb, taking his cigar out of his mouth and saying, with his irrestible chuckle, 'This is one of those rare and happy occasions when respectable people like you and I can enjoy pleasures normally reserved to the Irish Republican Army'."
Churchill was not Fiddling like Nero while Rome Burned, but was Commissioning a War Song while London Burned, page 303:
"On one occasion we were walking in the [late 1940 Chequers] garden with the Prime Minister [Churchill] late after dinner. London was being bombed and the eastern sky was red with the glare of great fires. The P.M. gazed at it sadly, shaking his head. Then he said unexpectedly that it was strange that this war, unlike the last, had produced no good songs - no Tipperary or Keep the Home Fires Burning. Someone suggested the Lambeth Walk, but that was held not to count because it was pre-war. 'I must write to Novello and tell him to produce a good war song,' said the P.M., and then, with the chuckle, 'but this time it will have to be Stop the Home Fires Burning'."
Slessor finishes his book on pages 636-7, stating that the the proven role of air power in WWII, in defeating enemy air power and "Germany's oil fuel" to pave "the way for the invasion", was finally incorporated into British defence policy by Churchill in his postwar Statement on Defence, Commandment 9391: "this deterrent must rest primarily on the stategic air power of the West, armed with its nuclear weapons. The knowledge that aggression will be met by overwhelming (emphasis added) nuclear retaliation is the surest guarantee that it will not take place."
ABOVE: Russian President Putin used exactly the same excuse for invading Ukrainian territory that Hitler used in his invasions (precise quotation is below): he just wants to enable his nationals abroad to have the "right" to join the Russian Federation, and he repudiates the notion that Ukraine is a soverign country because it is "just" an arbitrary political fabrication like Czechoslovakia was in 1938 (he could - and will soon - be saying that about the UN, USA, EU, UK, etc.). Russia should have been paid off at the end of the 1st Cold War in 1991, with some kind of Marshall Plan, as was used to safely demilitarise Germany, Japan et al in 1945. But the UK instead sent BP into Russia to help them develop high technology oil and gas supplies, which they now use against us. Russia is a corrupt, bankrupt superstate which now has its own oil and gas supplies, its own massive nuclear weapons infrastructure, and a rapidly depleting obsolete conventional weapons stockpile. There are many former USSR territories and other areas Putin can lay semi-spurious claim to, beyond Ukraine. Russia gained Warsaw, Poland, under the 1815 Vienna Settlement, losing it in 1918 when Poland became independent. Finland was gained by Russia from Sweden in 1809, Alaska became Russian territory in 1784 before being sold by the Tsar to USA, and so on. If Ukraine is "simply" surrendered to Russia, the way Chamberlain surrendered Czechoslovakia to Hitler (rewarding Nazis for aggression, using financial costs and fears of poison gas war as his excuse), WWWIII by deliberate "accident" or "miscalculation" will be far more likely than during the Cuban missiles crisis of 1962, when the West had a massive nuclear superiority over Russia! Gustav Bychowski's 1948 Dictators and Disciples explains dictatorship as an interdependence between the leader and the people, e.g. Stalin's war and territorial expansions (with help from propaganda) actually enhanced his reputation with his own people, and he really couldn't have cared less if the "capitalists" in the rest of the world disapproved.
ABOVE: telegrams from Sir Henderson, British Ambassador to Nazi Germany, to British Foreign Secretary Halifax, 22 February 1939 and 15 March 1939 (taken from Docs on Brit Foreign Policy, s3, v4, pages 593-5 linked online here), proving that even at that late time, freedom of criticism of the Nazis by certain (humane) elements of the British press and Jews (!) were still being blamed for Nazi evil, and this is some 4-5 months after Kristallnacht, and many years after Mein Kampf. Notice that Henderson writes that he would like to see Nazi Field Marshall Goering awarded a medal by the King to appease him (like his from the King for helping Chamberlain to give away Sudetenland to the Nazis 5 months earlier in exchange for Hitler's autograph!), then writes that he had sympathy with the Jews, but then immediately claims that the Jewish plight is "not a basis for policy for England." When Hitler broke the worthless Munich Agreement by invading the remainder of Czechoslovakia in March 1939, Henderson telegrammed Halifax: "What distresses me more than anything else is the handle which it will give to the critics of Munich." Well, not to Captain W. E. Johns, who was fired two months previously, from his editorships of Popular Flying and Flying on his orders, for criticisms of the government using subversive methods (government pressure on his publisher!). Let's now go back two volumes, and see what Henderson and Chamberlain did to try to start World War II (while lying about it) in 1938:
"If I am right, I do wish it might be possible to get at any rate 'The Times', Camrose, Beaverbrook Press &c. to write up Hitler as the apostle of Peace. It will be terribly shortsighted if this is not done. Cannot the News Dept. help? ... give Hitler as much credit as possible. The last word is his. We make a great mistake when our Press persists in abusing him. [He and Chamberlain "bravely" abused magazine publishers into getting Captain W. E. Johns fired from his position as editor of best selling magazines Popular Flying monthly and Flying weekly for calling for the deterrence of Nazi aggression by an arms race, in case their great lover Adolf Hitler was a trifle displeased with the British press! So much for liars who claim their exists "freedom of the press"!] ... If our only satisfaction is to slang him, then we must abandon hope of ever getting results."
- Sir Nevile Meyrick Henderson, GCMG (1882-1942), British Ambassador to Nazi Germany, Letter to Sir A Cadogan from the British Embassy in Berlin, 6 September 1938, reprinted as document 793 on page 257 of E. L. Woodward, Rohan Butler, and Margaret Lambert (editors), Documents on British Foreign Policy, 1919-1939, Third Series, Volume II, "1938", published in 1949 by His Majesty's Stationery Office, SBN-11-591527-3*. This particular volume doesn't appear to be available online yet, although it is the dynamite in the series! (I'm quoting this here to PROVE that there is nothing NEW in lying fascists in Western governments promoting racist fascism by secretly wining and dining - or coercing with threats of abuse if the velvet glove over the iron fist fails to work - the populist media into supporting terrorism against the Jews and others in the name of the Devil.)
"I reminded him [Adolf Hitler, during conversation at Berchtesgaden, 15 September 1938] that after 1914 it was said that if we had then told Germany that we would come in, there would have been no war ... He [Hitler] said a warning and a threat had the same effect. I dissented ... but I did not pursue this subject ... He said that he had from his youth been obsessed with the racial theory and he felt the Germans were one ... he is concerned with ten millions of Germans, three millions of whom are in Czechoslovakia. He felt therefore that those Germans should come into the Reich. They wanted to and he was determined that they should come in. Apart from that, he said, there was no other place where frontiers made any territorial difficulty. ... he was out for a racial unity and he did not want a lot of Czechs, all he wanted was Sudeten Germans."
- British Prime Minister Neville Chamberlain, BRITISH Minute of the Conversation between the Prime Minister and the Fuhrer, 15 September 1938 at Berchtesgaden, reprinted as document 895 at page 339 of E. L. Woodward, Rohan Butler, and Margaret Lambert (editors), Documents on British Foreign Policy, 1919-1939, Third Series, Volume II, "1938", published in 1949 by His Majesty's Stationery Office, SBN-11-591527-3*. (I'm quoting this here to PROVE that talking to evil devils provides you a load of lies, propaganda, and false promises.)
"He, Mr Chamberlain, must frankly admit that many Englishmen regarded the Fuhrer's speeches solely as words, behind which were concealed carefully prepared plans. He, Mr Chamberlain, however, regarded the Fuhrer as a man who, from a strong feeling for the sufferings of his nation, had carried through the renaissance of the German nation with extraordinary success. He had the greatest respect for this man ... After 1914 England had been reproached on many sides because she had not made her intentions clear enough. The war might perhaps heve been avoided, these critics objected, if England had taken a clearer attitude. ... The Fuhrer replied that ... after a certain moment, little could be done to change the unalterable course of events. In his opinion a British warning would have come too late in 1914 as well, since the difficulties had by then reached too advanced a stage."
- British Prime Minister Neville Chamberlain, GERMAN (Herr Schmidt, translator) Minute of the Conversation between the Prime Minister and the Fuhrer, 15 September 1938 at Berchtesgaden, reprinted as document 896 at pages 342 and 346 of E. L. Woodward, Rohan Butler, and Margaret Lambert (editors), Documents on British Foreign Policy, 1919-1939, Third Series, Volume II, "1938", published in 1949 by His Majesty's Stationery Office, SBN-11-591527-3*. (I'm quoting this here to PROVE differences between the BRITISH and GERMAN Minutes of the Conversation between Chamberlain and Hitler at Berchtesgaden, 15 September 1938!)
"Herr Hitler said [to Chamberlain at Godesberg, 22 September 1938] that he would like to thank the Prime Minister for his great efforts to reach a peaceful solution. He was not clear, however, whether the proposals, of which the Prime Minister had just given him an outline, were those submitted to the Czechoslovak Government. The Prime Minister replied: Yes. Herr Hitler said he was sorry, since those proposals could not be maintained. ... Czechoslovakia was an artificial construction, which was called into being and was established solely on the grounds of political considerations." [Cf. Putin's description of Ukraine, DUH!]
- Note of a Conversation between Mr Chamberlain and Herr Hitler at Godesberg, 22 September 1938, reprinted as document 1033 at page 465 of E. L. Woodward, Rohan Butler, and Margaret Lambert (editors), Documents on British Foreign Policy, 1919-1939, Third Series, Volume II, "1938", published in 1949 by His Majesty's Stationery Office, SBN-11-591527-3*. (I'm quoting this here to PROVE what happens when you are such an EGOTIST you think you can "negotiate" a "peace agreement" with the Devil!)
"The Prime Minister [Chamberlain, at the Munich Conference with Hitler on 29 September 1938] pointed out that he could not give such a guarantee [for the Sudeten evacuation of Jews by 10 October 1938 for FAST Nazi annexation] ... This led to a tirade from Herr Hitler (who was otherwise calm throughout most of the Conference), his line being that if - having asked him to stay his hand - we were not prepared to take the responsibility of ensuring the concurrence of Czechoslovakia we had better let him resume his way!"
- Note by Sir Horace Wilson on the Munich Conference, between Chamberlain and Hitler, 29 September 1938, reprinted as document 1227 at page 631 of E. L. Woodward, Rohan Butler, and Margaret Lambert (editors), Documents on British Foreign Policy, 1919-1939, Third Series, Volume II, "1938", published in 1949 by His Majesty's Stationery Office, SBN-11-591527-3*. (I'm quoting this here to PROVE that once you start on the road to diplomacy with a Devil who takes a mile whenever you give an inch, it becomes worse than the script for an unfunny, depressing episode of Monty Python's Flying Circus. It's worse than the dead parrot sketch!)
"Herr Hitler [to Chamberlain, in Hitler's Munich Flat, 30 September 1938]: Years ago he [Hitler] made proposals for the restriction of the use of the air arm. He himself fought in the Great War and had a personal knowledge of what air bombardment means. It had been his intention, if he had to use force, to limit air action to front line zones as a matter of principle ... he would always try to spare the civilian population and to confine himself to military objectives. ... Herr Hitler: The situation about air disarmament is just the same as it is in the case of the naval situation. If a single nation refuses to agree, all the others have to follow her example. [Secretly-rearming fascists agree to PAPER "disarmanent" for the concessions involved like lifting sanctions etc, but then secretly break the agreement! DUH!] One sees what has happened in the case of the Naval Treaty. When Japan refused to agree, all the other nations had to give up their restriction. It would be just the same if one tried to abolish bombing aircraft. ... He himself [Hitler] had proposed years ago- 1. The abolition of bombing aircraft; 2. If '1.' could not be accepted, the abolition of bombing outside a zone of 15 to 20 km from the front line; and 3. If neither '1.' nor '2.' were accepted, the limitation of bombing to a zone which could be reached by heavy artillery. ... The development of bombing from the air [Hitler declared] extends the horrors of war to the non-combatant population and is therefore a barbarism."
- Note by Dr Schmidt of a Conversation between the Prime Minister and Herr Hitler, at the latter's Flat in Munich, 30 September 1938, reprinted as document 1228 at pages 636 and 638 of E. L. Woodward, Rohan Butler, and Margaret Lambert (editors), Documents on British Foreign Policy, 1919-1939, Third Series, Volume II, "1938", published in 1949 by His Majesty's Stationery Office, SBN-11-591527-3*. (I'm quoting this here to PROVE that negotiating with dictators is a complete farce; they are experts on "peacemaking" and "disarmament" propaganda lying scams and will turn the tables verbally and appear to be the heroes of liberty! It was at the end of this very meeting that Chamberlain did his "magician act" of plucking a piece of paper from his pocket which outlawed war between the Nazis and British, and they both signed it, which naturally prevented WWII, just as intended! Duh! Wicked diplomacy! It is LINKED HERE with a snap of Chamberlain celebrating his "success" back home from the window of his flat above 10 Downing Street, a fraudulent travesty of propaganda lying which he called "peace in our time", but which would certainly have "earned" him a few dozen Lordships and Nobel peace prizes, if it hadn't been a staged farce.)
"After emphasising that the gathering was a confidential one, and that nothing was to be quoted as official, the Prime Minister [Chamberlain, speaking CONFIDENTIALLY to the "British Press" on 11 September 1938, in a typical travesty of the populist claims about "freedom of the press" etc.] said: ... War ... is something which might in the very first few hours affect the civilian population. Thereby it becomes an even more dreadful and horrible thing than it was before. The Government's policy and the Government's efforts are directed all the time to the avoidance of any such catastrophe as that [a complete lie since slow rearmament plus appeasement encouraged war as these thugs had been told repeatedly by Captain W. E. Johns in Popular Flying and Flying editorials, but they had used backhanded techniques to shut up Captain W. E. Johns by getting him fired via subversive pressure on his publisher, proving them narcissistic lying fascist-technique thugs]."
- Text of the Prime Minister's Statement to the Press on September 11, 1938, reprinted as Appendix III at pages 680 of E. L. Woodward, Rohan Butler, and Margaret Lambert (editors), Documents on British Foreign Policy, 1919-1939, Third Series, Volume II, "1938", published in 1949 by His Majesty's Stationery Office, SBN-11-591527-3*. (This book can be read like a depressing thriller in a few hours, but we're quoting it here because, unlike history books full of 2nd-hand controversial opinions based on BS like A. J. P. Taylor's "history", it is purely a primary source of actual meeting transcripts, and it is as hard to get your hands on probably due to its expense and people in 1949 Britain wanting to "move on" from the 1930s "appeasement" disaster. Again, as repeatedly pointed out on this blog, appeasement is a wonderful thing and not a problem UNLESS you do it through coercive fear about being wiped off the face of the earth in a 1930s imaginary poison gas cloud, or a 1950s over-hyped nuclear radioactive fallout cloud (all such hyped up "threats" can be easily countered, as we will see in this post, later below). Kennedy made the point in 1940 in Why England Slept that appeasement was not a tragic policy; the bad policy was instead a REFUSAL to rearm FASTER than your opponent, simply out of fear of upsetting your opponent or triggering a first strike against yourself if you don't appease the enemy. Coercion is the problem, not "appeasement". By all means appease if you have might on your side and can afford to give favours, just don't do it out of WEAKNESS to encourage your opponent to keep advancing until your back is against the wall, fighting on your opponent's terms.)
ABOVE: compiler of this blog post, anti-nuclear-disarmament (aka Marx-war-for-global-communist-and-peace-through-classwar-and-racewar-and-nuclear-war) liars, anti-fascist activist Nige Cook, holding the fascist Marx-media to account for causing the Ukraine War since 2006 on this blog with his dad (who took the photo) and author of the 1990-4 Nuclear Weapons Effects Theory (censored from publication by Cambridge Uni press's Simon Mitten, Oxford Uni press's Donald Degenhardt, and all the various hyper left wing anti-nuclear lying newspaper editors in the UK, all duped simpletons who believed disarmament Glasstone or Nukemap style populist liars for "peace" aka russian racewar/classwar/nukewar/eurowar/corbynwar).
ABOVE (VIDEO CLIP): Russian State TV Channel 1 preparing Russians mentally for nuclear war (they already have nuclear shelters and a new Putin-era tactical nuclear war civil defense manual from 2014, discussed later in this blog post) arguing for use of nuclear weapons in Ukraine war in 2023: "We should not be afraid of what it is unnecessary to be afraid of. We need to win. That is all. We have to achieve this with the means we have, with the weapons we have. I would like to remind you that a nuclear weapon is not just a bomb; it is the heritage of the whole Russian people, suffered through the hardest times. It is our heritage. And we have the right to use it to defend our homeland [WFT does he mean, the liberated components of the USSR that gained freedom in 1992?]. Changing the [nuclear use] doctrine is just a piece of paper, but it is worth making a decision."
BELOW: extracts from the unclassified-yet-censored-for-publication "limited distribution" American government book by John Northrop (Handbook of Nuclear Weapon Effects Abstracted from EM-1, a few pages are linked here to give the flavour of it, without publishing the entire document which might contain some sensitive data somewhere, and it would take scanning time that I don't have anyway), effectively replacing Glasstone's 1977 lies book on nuclear weapons. The terrible Carter admin politically correct – i.e. trash – 1977 version of Glasstone’s book, The Effects of Nuclear Weapons, deletes all the useful data on protective measures nuclear tests in previous versions, creating the delusion that a nuclear bomb on an unobstructed desert creates the same effect as in a highly shielded concrete city, where buildings PROVABLY absorb all the effects – radiation and also blast as proved by Lord Penney to the continuing horror of the Pentagon’s nuke disarmament freaks – VERY effectively, reducing casualties by a factor on the order of 100 from what you get for Glasstone’s assumption of nukes over nudist beaches! This is an exact duplication of Britain's gas warfare lying establishment in the 1920s-30s, which refused to engage in public arguments on weapons of mass destruction to debunk lying fascist disarmament and arms control liars, who wanted a world war or peaceful Nazi world domination, not credible deterrence with honest, simple civil defense to make it credible. Over 40 years ago, Samuel Cohen's neutron bomb "controversy" raged: because modern city concrete and steel buildings are blast and heat resistant (unlike the wooden houses with charcoal stoves prevailing in Hiroshima and Nagasaki in 1945), you can detonate a nuclear weapon at a height that eliminates modern city damage and fallout dust, but that still causes non-lethal EMP or a lethal neutron flash to stop operations by an opponent. So nuclear weapons can be used to credibly deter the invasions that set off the world wars (Belgium 1914, Poland 1939). The CND/Corbyn claim that there will be uncontrolled automatic nuclear escalation from counterforce to countervalue attacks on civilians is like the claim of inevitable gas war knockout-blow city gas war escalation: gas knockout blow escalation was disproved.
ABOVE: notice the thermal flash self-shielding of wheat fields from thermal radiation! In reality, anything inflammable merely smokes from the ablation of the outer 0.1mm or so of inflammable material, and thus creates its own protective smokescreen that prevents fires, and nuclear weapons don't ignite anything unless things are practically self-combusting anyway. In very dry weather with a shifting direction breeze, one discarded barbecue can set off a mass fire, without need for any nuclear bombs: the results are identical as per the Arabian proverb, a forest only burns due to its own trees. Nuclear weapons thermal pulses are so short, unlike say the K-T impact explosion around 65 million years ago, that they can only dry out a very thin surface layer of humid "inflammable" (when dry) materials like vegetation. This was proved by studies of the forest stands on Bikini and Eniwetok during and after multimegaton nuclear tests (photos linked here; taken from Glasstone 1957 and removed corruptly and dishonestly from future propaganda not fact based editions). Sure, you get smoke without fire from nuclear weapons thermal radiation, but that smokescreen arises rapidly near ground zero and so shields targets ar greater distances. The existence of an artificial skyline of concrete buildings in the "concrete jungle" of modern cities - unlike Hiroshima and Nagasaki which were mostly single storey wood frame buildings - has a similar effect as proved by British nuclear tests civil defence effectiveness researcher George R. Stanbury, who was ignored for decades for political propaganda reasons by the Pentagon. Dad, an advanced civil defence corp instructor, met Stanbury during a residential course at the civil defence staff college, Easingwold, Yorkshire (having special authority from Essex's Civil Defence chief, to attend as the course was usually for full-time employees only), and later corresponded with British nuclear test and Hiroshima and Nagasaki blast effects expert William G. Penney on blast shielding by cities by blast; he found that both knew that their own specialised effect - thermal and blast, respectively - was exaggerated, but both falsely believed that the other effect. Stanbury "knew" blast was the problem because skyline shielding would stop the radiation and getting people to simply toss wet paper on their fires on the attack warning siren would create an effective smokescreen to stop scattered thermal ray fires/burns, while Penney knew that the blast absorption by damage done in modern cities would kill the blast, but thought the thermal flash would start firestorms because he hadn't bothered to investigate ther firestorm mechanism in Hiroshima and had been misled to lies from the Americans on this. Consequently, neither felt inclined to launch a full-on assault on the Pentagon's nuclear weapons effects mythology!
block; padding: 1em 0; text-align: center; clear: left; float: left;">

ABOVE: Russian mobile nuclear missile launchers can move quickly enough to get out of the ~4 psi peak overpressure blast zone (needed to overturn them, provided the blast hits them side-on and not head-on), during the time American Minuteman or Trident missiles are in flight to targets located well inland in Russian territory, e.g. Siberia. Hence, we have toss all deterrence, even if they all get dementia and decide NOT to launch-on-warning in an intense East-West crisis! Duh. Duh. Duh! We'll discuss this in more detail later. EM-1 contains a mathematical model allowing detailed calculations of blast wind pressure induced overturning of mobile missile launchers based on their size and mass, but as we've just pointed out, they can reduce vulnerability simply by moving off when a USA launch is detected, and then turning to face their previous position, and extending their stabiliser/outrigger foot pads. "Simples!", as the Meerkats say in UK TV ads. We have no credible deterrent whatever. We'll discuss this problem of mobile Russian ICBM and tacticla nuclear warhead launchers later in more detail in this post (below).
ABOVE: weapon type 13 in this table of neutron and gammas output spectra from various warheads (the table shows only 4 types out of 13 in EM-1) shows precisely the output from the W79 enhanced-neutron capable tactical deterrent, the only thing we ever had to counter 2000+ Russian neutron bombs. One little snag: we don't have ANY W79's. They were flushed down the pan along with Ukraine's nuclear deterrent. Second little snag: the LOWEST neutron output weapon is type 10 in EM-1 and is conveniently not included in Northrop's summary table above! Guess what the hell the type 10 is? Yup. You guessed right: the primary-only ("tactical") option on the B61's dial-a-yield. The W79 or "type 13" neutron bomb air burst at 500 m altitude gives a dose at ground zero of 170,000 rads of neutrons plus 27,200 rads of secondary gamma rays, according to EM-1. At the other end of the scale, the lowest neutron dose, just 0.666 rads, is produced by the type 10 in EM-1, the low-yield fission primary stage "dial a yield" option of a B61 thick-cased thermonuclear weapon having multiple yield options. This is because the casing on a weapon with high yield options absorbs most of the neutrons from the primary stage, and thereby shows that you cannot simply use the low-yield option on a B61 as a replacement for tactical nuclear weapons like neutron bombs. USA nuclear warhead designers have lied to the public and the president about this to make the West vulnerable to Russian coercion, an infiltration by traitors which makes the Wen Ho Lee "scandal" about data leaked to China look like a storm in a teacup (the USA has declassified some B61 design detail, shown later below).
"William J. Broad: Ukraine gave up a giant nuclear arsenal 30 years ago. Today there are regrets. At the end of the Cold War, the third largest nuclear power on earth was not Britain, France or China. It was Ukraine. The Soviet collapse, a slow-motion downfall that culminated in December 1991, resulted in the newly independent Ukraine inheriting roughly 5,000 nuclear arms that Moscow had stationed on its soil. Underground silos on its military bases held long-range missiles that carried up to 10 thermonuclear warheads, each far stronger than the bomb that leveled Hiroshima. Only Russia and the United States had more weapons." - https://kyivindependent.com/hot-topic/william-j-broad-ukraine-gave-up-a-giant-nuclear-arsenal-30-years-ago-today-there-are-regrets
DISARMAMENT WARMONGERING RESULTS: (1) Disarmament via agreement (ignoring for now the 30 September 1938 UK-Nazi signed peace pact, etc) was disproved by Putin when - despite being signed up to the Chemical Weapons disarmament conventions, he ILLEGALLY BROKE THE DISARMAMENT AGREEMENTS and used chemical weapons, not just sarin nerve agent to help Assad win in Syria, but the latest most lethal Russian agent, Novichok, in the UK in 2018 to murder Dawn Sturgess (please see our blog post chronology at the time of the attack and analysis of Russian lying propaganda on disarmament, linked here). If he does that for Novichok, he can do it for tactical nuclear weapons! In WWII nuclear weapons were even made in secret from scratch by a democracy which had never made a nuclear weapon and wasn't even sure if it was possible, and then used on a nuclear unarmed state during the war, despite the democracy in question not having stockpile containing a single nuclear weapon when the war started! So this proves that 100% total disarmament can't stop a nuclear war! Unbelievable fact, that, according to the simplistic, fake news and smug disarmament lies you read in the papers and see on fascist style SIPRI lying TV murderers of kids through disarmament to prevent the credible deterrence of war, isn't it? Thus, paper agreements with the entire class of lying thug dictatorships that use WMDs to win a war against you, are useless. Hoping Hitler would cover himself shame if he violated agreements wasn't a good military policy, but it was used by thugs who clearly wanted a war in the 1930s and were rewarded with peace prizes in consequence (Angell and Philip Noel-Baker were the worst of the lot; the latter was made a Lord and continued to splutter lies for disarmament in 1980 in the House of Lords with no opposition, as we'll expose later in this post). The counter-argument that signed up agreements are rarely broken between democracies is vacuous because as Weart proved in Never At War years ago, democracies don't fight one another. In other words, the only situation in which written laws stop wars or crimes is for lad-abiding people who don't start wars or commit crimes! The only situation where wars or crimes can occur is for despots and criminals, who break agreements and laws! So bits of paper are no substitute for credible deterrence of dictators. The whole basis for "arms control" and "disarmament" is as fake a Angell's faked Great Illusion "disprove" of arms-races to avoid wars, which led to precisely what he claimed to avoid. See Joad's 1939 Why War for how Angell used his "arms race" lie to counter Churchill's pre-WWI call for superiority to deter the Kaiser, and see President kennedy's Why England Slept to see how Angell's arms-race lie was used by Grey to excuse his failure to deter WWI, and how disarmers used that arms race lie repeatedly throughout the 1920s and 1930s to set off WWII, by ensuring Britain avoided an arms race with the Nazis, by rearming slower than the Nazis to avoid giving Hitler any excuse to set off WWII - by the way, this was 100% successful and Hitler didn't declare war on the UK first, it was the UK that finally had to declare war because appeasement allowed virtually bloodless invasions and cold-blooded genocide!),
(2) unilateral nuclear disarmament for guaranteed peace! Wonderful idea. But Japan was in a nuclear unarmed position in August 1945, and it did not take a Hitler or a Putin or even a Republican to drop not one but two nuclear weapons on it. Democratic President Harry Truman didn't hesitate to "press the metaphorical button" against a country which lacked nuclear weapons, just as the USA presently lacks even a single credible, tactical enhanced radiation-capable W79 warhead (if Putin gets his way we find out what Hitler might have done with 2000+ tactical neutron bombs against a USA which now hates Kennedy's Why England Slept).
(3) HISTORY SHOWS THE ONLY COUNTRY TO HAVE BEEN ATTACKED WITH NUCLEAR WEAPONS (AUGUST 1945) DID N-O-T HAVE ANY NUCLEAR WEAPONS. BEING NUCLEAR UNARMED DIDN'T SAVE IT FROM BEING NUKED. Moreover, the pre-war stockpiles that disarmers concentrate on minimising are almost purely FOR DETERRENCE, as easily proved by dividing those pre-war (pre WWI and pre WWII) weapons stockpiles into the total munitions used in wars. In other words, the number of pre-war weapons you have has jack ---- relation to the number of weapons used in the war you fail to credibly deter! This COMPLETELY DISPROVES THE "ARMS RACE" CAUSES SLAUGHTER MYTHS OF WWI AND WWII! The weapons that flattened the wooden houses (not concrete buildings in general, or air raid shelters in general) in Hiroshima and Nagasaki, and that burned the wooden medieval slums of Hamburg, were made DURING THE WAR, not in the non-existent "arms race" prior to the war. (Let that fact sink in for 24 hours before you read Glasstone or play with Nukemap, or head "history" written by Russian biased Marxists like A. J. P. Taylor and Adolf Hitler. Don't trust those Nazis, the're unreliable due to bias!)
(4) GLASSTONE/NUKEMAP IGNORE THE SINGLE MOST IMPORTANT USE/EFFECT OF NUCLEAR WEAPONS: DETERRENCE IS AN EFFECT OF NUCLEAR WEAPONS AND A USE OF NUCLEAR WEAPONS THAT YOU IGNORE AT YOUR PERIL, AND AT THE PERIL OF UKRAINIAN KIDS, AND IN FUTURE, THE LIVES OF AMERICAN KIDS WHO YOU INSTRUCT NOT TO DUCK AND COVER AND NOT TO HAVE A DETERRENT THAT IS CREDIBLE! This is all Russian Cold War anti-Western civil defence lying! Russia was (and is) totally pro-civil defence just as it is and was always pro-nuclear; the anti-civil defence stuff and anti nuclear stuff from Russia and its comintern comrades in the Western Marx Media is a trick to undermine Western defence, enabling Russian superiority; unfortunately people like Hans Bethe and the entire Western "arms control and disarmament" organization fails to appreciate the con-trick and hypocrisy from Russia on this. As a result, the effects of nuclear weapons have been totally distorted by Glasstone / Nukemap propaganda on behalf of pseudo (fake news) "Arms Control" liars who are effectively fellow travellers of Putin's agents in the media: nuclear weapons in the Kennedy era were used to try to de-escalate crises, e.g. USA had a large nuclear superiority at the time of the October 1962 Cuban missiles crisis and in his 22 October 1962 television address to the American people, Kennedy was able to use that nuclear superiority to deter what the Marx media call nuclear "accidents" (deliberate carelessness or contrived attacks under the name of a "that was JUST a mistake - SORRRRRREEEEY, now I've said sorry shut the ---- up about it or you'll start a REAL war, matey!"). Guess what? "Arms Conrol" mass-murderers with kid's blood soaked hands who caused all the wars that should have been credibly deterred by USING TACTICAL NUCLEAR WEAPONS TO CREDIBLY DETER WAR, refuse to acknowledge, assess, or respect the true fact that kennedy used nuclear superiority in 1962 and that parity and inferiority encouraged genocide by the Nazis! What newspaper or TV station in the corrupt West will publish this? None. They're all determined to soak their hands repeatedly in blood so they can report mass murders, not deter war (a newsroom "non-event: move along please, nothing to see here" that doesn't exactly "boost viewing figures or sell toilet paper").
GLASSTONE'S EFFECTS OF NUCLEAR WEAPONS UNOBSTRUCTED TERRAIN DATA DEBUNKED FOR STRATEGIC COUNTERVALUE DETERRENCE
If you're sick of reading rubbish on nuclear effects by authors who defend Russian aggression as a reaction against Western imperialism, and that the Ukraine war proves we must disarm now to prevent nuclear deterrence of WWIII (some gung-ho military folk will endorse that, too, seeing some kind of fun to be had in the hell of a conventional WWIII or more likely surrender and then an unelected "world government for peace" of the Brezhnev variety), then one really good, well informed nuclear weapons history (unlike the Hiroshima effects lies and propaganda about people with no feet running around in Hiroshima quoted uncritically by Mr Rhodes et al.), albeit subjected to a hate rant by Carey Sublette ("Most of the text that is not Shelton’s actual recollections or direct commentary is lifted verbatim from government reports"), who also runs a site promoting lying ignorant crap about nuclear weapons designs and effects over unobstructed deserts being applicable to modern city targets and who falsely claimed it contained plagiarism (it doesn't, and the Nukemap guy also deleted a comment by me pointing out that Feynman does write about what he actually did at Los Alamos - e.g. running the implosion calculations on IBM mechanical card sorters - in one of his books, after the Nukemap guy had attacked Feynman for allegedly not being clear), is the Shelton's Reflections of a Nuclear Weaponeer (very brief extract of under 5% of the book is linked here, just to give the flavour), particularly the 2nd edition of 1990 which has enlarged page litho printing (it's literally the size and mass of a good old fashioned Church Bible) and contains vital updates like color photos supplied by Agnew, and also in the last notes section, Lord Penney's endorsement of the 1st edition. Shelton (October 4, 1924 - November 27, 2014) doesn't pander to the USSR, their spies, or radiation orthodoxy. He writes that by helping to credibly deter WWIII, the bomb proved useful and we don't need to forget that. Not a message Putin and his friend thugs in Western "arms control and disarmament" seem to appreciate.
Also in living memory (but now practically entirely deleted from the mainstream pseudo-"history" of the appeasement, disarmament, collaborate-with-thugs-for-peace-not-nuclear-deterrence pseudo-"communists") is Andrei Sakharov’s Memoirs (Knopf 1990), which details the gulag and psychiatric treatment provided by the CCCP for dissidents.
Sakharov was exiled with his wife to Gorky by Brezhnev for criticising the latter’s decision to invade Afghanistan at the end of 1979. He was there relentlessly persecuted by the KGB and went on repeated hunger strikes for 7 years until Gorbachev released him. His statement of 27 January 1980 (Appendix B of his Memoirs, pp. 673-5):
“On January 22, I was detained on the street and taken by force to the USSR Procurator’s office ... I was asked to return the medals and orders and certificates ... Rekunkov also informed me of the decision to banish me to the city of Gorky, which is closed to foreigners ... I was instructed to report three times a month to the police ... The authorities are completely isolating me from the outside world. The house is surrounded 24 hours a day by police and the KGB, who keep away all visitors, including my friends. Telephone connections with Moscow and Leningrad are cut off. We have not even been able to call my wife’s mother ... Even in prison, there is more possibility of communication with the outside world ... The worsening of the international situation was caused by the following actions of the USSR ... Supporting terrorist regimes ... Supporting the actions of quasi-governmental terrorists in Iran who have violated diplomatic immunity ... the invasion of Afghanistan ...”
(That time, we still had the W79 neutron bomb, the threat of tit-for-tat retaliation if Russia tried to escalate to win that war. Please listen to the 1951 Jackie Doll and his Pickled Peppers song opposing Truman's decision to nuke CIVILIANS in Japan but NOT fascist troops in Korea. General McArthur gave Truman his firm MIDDLE FINGER AND RESIGNED IN PROTEST, like the DECENT OLD SOLDIER HE WAS. Killing off Joe Stalin in 1951 instead of appeasement could have saved millions in Korea, Vietnam, Afghanistan, Iraq and now Ukraine - and note that the military casualty figures for the "Ukraine War" are BS, since they don't include all those elderly Europeans killed by the rising cost of heating fuel and food - due to the war cutting cheap oil and gas supplies. Millions are being slowly murdered by those fascist pseudo-communists; if they want TRUE COMMUNISM start by BEING TRUTHFUL and F=== OFF with the mass murdering wars, F=== OFF with the endless Orwellian doubletalk S=== PROPAGANDA, and F=== OFF killing the Jews to try to steal their money to fund DICTATORSHIPS OF EVIL disguished as socialist or communist utopias.)
ABOVE: Nigel Farage (who ran the Brexit Campaign in UK that got the UK out of the dictatorial EU which was desperately and "secretly" trying to start WW3 with Russia in order to create a Communist Dictatorial "Utopia" of anti-Individualism from the radioactive rubble in the aftermath) reinventing himself as Lord Halifax circa 1940, in demanding we ask Putin "what price peace?" I unfortunately feel the need to respond to Mr Farage. Farage, you correctly called for a new British Civil Defence Corps back in February 2014, complaining about Marxist PM Harold Wilson's decision to scrap it to curry favour with his Labour Party militant Marxists (who wanted WW3 and Russian annexation) in 1968, so why are you NOT doing this now? Don't you know the facts on this blog? And why aren't you calling for NATO to expand and for tactical neutron bombs in every one, to deter, stop and prevent a repetion of the invasions in Europe that sparked each World War (invasion of Belgium by concentrated force in 1914, invasion of Poland by concentrated Russian and German force in 1939). Why are you calling for a repeat of the 30 September 1938 "peace deal" between Chamberlain and Hitler? Why? Are you that ignorant of the history of civil defence effectiveness, tactical nuclear war deterrence, and appeasement being used by dictatorships to inure their peoples in the need for aggressive actions that can only escalate into mass murder? In an ideal world, Ukraine would secretly assassinate Putin; sadly this was attempted 42 times with Hitler and failed, so don't hold your breath.
Update (19 January 2024): Jane Corbin of BBC TV is continuing to publish ill-informed nuclear weapons capabilities nonsense debunked here since 2006 (a summary of some key evidence is linked here), e.g. her 9pm 18 Jan 2024 CND biased propaganda showpiece Nuclear Armageddon: How Close Are We? https://www.bbc.co.uk/iplayer/episode/m001vgq5/nuclear-armageddon-how-close-are-we which claims - from the standpoint of 1980s Greenham Common anti-American CND propaganda - that the world would be safer without nuclear weapons, despite the 1914-18 and 1939-45 trifles that she doesn't even bother to mention, which were only ended with nuclear deterrence. Moreover, she doesn't mention the BBC's Feb 1927 WMD exaggerating broadcast by Noel-Baker which used the false claim that there is no defence against mass destruction by gas bombs to argue for UK disarmament, something that later won him a Nobel Peace Prize and helped ensure the UK had no deterrent against the Nazis until too late to set off WWII (Nobel peace prizes were also awarded to others for lying, too, for instance Norman Angell whose pre-WWI book The Great Illusion helped ensure Britain's 1914 Liberal party Cabinet procrastinated on deciding what to do if Belgium was invaded, and thus failed deter the Kaiser from triggering the First World War!). The whole basis of her show was to edit out any realism whatsoever regarding the topic which is the title of her programme! No surprise there, then. Los Alamos, Livermore and Sandia are currently designing the W93 nuclear warhead for SLBM's to replace the older W76 and W88, and what she should do next time is to address the key issue of what that design should be to deter dictators without risking escalation via collateral damage: "To enhance the flexibility and responsiveness of our nuclear forces as directed in the 2018 NPR, we will pursue two supplemental capabilities to existing U.S. nuclear forces: a low-yield SLBM warhead (W76-2) capability and a modern nuclear sea launched cruise missile (SLCM-N) to address regional deterrence challenges that have resulted from increasing Russian and Chinese nuclear capabilities. These supplemental capabilities are necessary to correct any misperception an adversary can escalate their way to victory, and ensure our ability to provide a strategic deterrent. Russia’s increased reliance on non-treaty accountable strategic and theater nuclear weapons and evolving doctrine of limited first-use in a regional conflict, give evidence of the increased possibility of Russia’s employment of nuclear weapons. ... The NNSA took efforts in 2019 to address a gap identified in the 2018 NPR by converting a small number of W76-1s into the W76-2 low-yield variant. ... In 2019, our weapon modernization programs saw a setback when reliability issues emerged with commercial off-the-shelf non-nuclear components intended for the W88 Alteration 370 program and the B61-12 LEP. ... Finally, another just-in-time program is the W80-4 LEP, which remains in synchronized development with the LRSO delivery system. ... The Nuclear Weapons Council has established a requirement for the W93 ... If deterrence fails, our combat-ready force is prepared now to deliver a decisive response anywhere on the globe ..." - Testimony of Commander Charles Richard, US Strategic Command, to the Senate Committee on Armed Services, 13 Feb 2020. This issue of how to use nuclear weapons safely to deter major provocations that escalate to horrific wars is surely is the key issue humanity should be concerned with, not the CND time-machine of returning to a non-nuclear 1914 or 1939! Corbin doesn't address it; she uses debunked old propaganda tactics to avoid the real issues and the key facts.
For example, Corbin quotes only half a sentence by Kennedy in his TV speech of 22 October 1962: "it shall be the policy of this nation to regard any nuclear missile launched from Cuba against any nation in the Western hemisphere as an attack by the Soviet Union on the United States", and omits the second half of the sentence, which concludes: "requiring a full retalitory response upon the Soviet Union." Kennedy was clearly using US nuclear superiority in 1962 to deter Khrushchev from allowing the Castro regime to start any nuclear war with America! By chopping up Kennedy's sentence, Corbin juggles the true facts of history to meet the CND agenda of "disarm or be annihilated." Another trick is her decision to uncritically interview CND biased anti-civil defense fanatics like the man (Professor Freedman) who got Bill Massey of the Sunday Express to water down my article debunking pro-war CND type "anti-nuclear" propaganda lies on civil defense in 1995! Massey reported to me that Freedman claimed civil defense is no use against a H-bomb, which he claims is cheaper than dirt cheap shelters, exactly what Freedman wrote in his deceptive letter published in the 26 March 1980 Times newspaper: "for far less expenditure the enemy could make a mockery of all this by increasing the number of attacking weapons", which completely ignores the Russian dual-use concept of simply adding blast doors to metro tubes and underground car parks, etc. In any case, civil defense makes deterrence credible as even the most hard left wingers like Duncan Campbell acknowledged on page 5 of War Plan UK (Paladin Books, London, 1983): "Civil defence ... is a means, if need be, of putting that deterrence policy, for those who believe in it, into practical effect."